Formulae for Geodetic Computations on a Spheroid : Some History
by Paul Wise, 2023
Introduction
Accurately depicting, on a flat sheet of paper, information about natural and manmade features on the curved surface of the Earth, in other words to make a map, drove the need to represent the Earth’s curved surface by some mathematically defined figure. Over small areas the Earth’s curvature could be safely ignored. For national purposes, however, the best possible relativity over hundreds or even several thousands of kilometres, was required. Thus, from a starting point all the survey measurements and calculations would need to be of such quality that if the survey looped to close back on its starting point the difference between the original starting coordinates and those obtained via the survey would always fall within a very small, specified, tolerance.
Such surveys were based on a network of adjoining triangles or triangulation. In these surveys all the internal angles of the triangles were observed and with the length of one triangle side measured the remaining triangle sides could all be calculated.
When does the Earth’s Curvature become a Factor
As the length of the sides of a triangle increased over a curved surface, the triangle could no longer be considered planar, where its three internal angles equalled 180 degrees, but must be considered spherical. In a spherical triangle, the sum of its three internal angles now equalled 180 degrees plus an amount called spherical excess (ε). By evaluating the amount of spherical excess from the dimensions and angles of a triangle it was possible to provide a guideline as to when a triangle may be considered planar or must be considered spherical. In general, it was considered that spherical excess increased by 1 arc second for every 75 square miles (200 square kilometres) of area, meaning that a right angled triangle with sides of 15 and 25 kilometres (10 miles and 15 miles) respectively would have had 1 arc second of spherical excess.
There were several formulae for calculating spherical excess. L'Huilier's Theorem, regarded as the most accurate, required that the length of the three sides be known. In their Manual of Geodetic Triangulation, the US Coast and Geodetic Survey (1959), defined a more practical formula for field party use, as shown below.
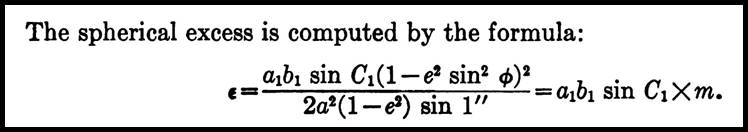
In this formula ε was the spherical excess; a1, b1, and C1 were two side distances and the included angle, respectively, of the corresponding triangle. The term m comprised values for the applicable spheroid based on the mean latitude of the three vertices of the triangle. Initially logarithmic tables were available such that the value for m could be easily extracted. This formula was accurate to one one hundredth of an arc second for an equilateral triangle with 200 kilometre (300 mile) long sides, or for a non equilateral triangle of the same area.
In hindsight, many of the early triangulations, despite the efforts they entailed and their advancement of technology, were later shown to have the fundamental flaw of not accounting for spherical excess.
Triangulation Reduction and Calculation
For each triangle of the triangulation a standard process was later adopted whereby the internal angles of a triangle were adjusted to account for spherical excess, if any, as well as any observational error. After determining the value of spherical excess for the specific triangle, the value for spherical excess was deducted from the sum of the three internal angles. Any difference from 180 degrees was now observational error and could be distributed between the three angles by simply applying one third of the error to each angle or similar. Now one third of the value for spherical excess, if any, was deducted from each angle to reduce them to their plane values. A numerical example is shown below where the triangle is assumed to have a spherical excess of 3 arc seconds.
|
|
Observed angles |
Corrected angles |
Planar angles |
|
59° 59’ 59” |
59° 59’ 58” |
59° 59’ 57” |
|
|
Angle B |
60° 00’ 05” |
60° 00’ 04” |
60° 00’ 03” |
|
Angle C |
60° 00’ 02” |
60° 00’ 01” |
60° 00’ 00” |
|
Sum of A+B+C |
180° 00’ 06” |
180° 00’ 03” |
180° 00’ 00” |
|
Spherical excess ε |
3” |
3” |
Check |
|
Spherical excess deducted |
180° 00’ 03” |
Check |
|
|
Difference from 180 degrees |
180° 00’ 00” |
1/3 ε or -1” to each angle |
|
|
Observational error |
3” |
|
|
|
1/3 correction to each angle |
-1” |
|
|
Once the planar angles were determined the computation of the lengths of the sides of each triangle, from one known (previously determined) length and the three determined angles, was by the Law of Sines being :
Side a/Sine angle A = Side b/Sine angle B = Side c/Sine angle C,
Commonly, a/Sine A = b/Sine B = c/Sine C.
On the basis that length of side a and the three angles A, B, C were known for each triangle, then the lengths of sides b and c were determined from :
b = (a/Sine A) * Sine B and c = (a/Sine A) * Sine C, and at a time when all such calculations were done by hand using logarithms the formulae thus became :
log b = (log 1 – log sine A) + log sine B + log a, and
log c = (log 1 – log sine A) + log sine C + log a.
By then adopting a standard layout, the repetitious writing of values was avoided saving time and transcription mistakes. Apart from one subtraction operation all other operations were additions. Please refer to the example below where the columns and rows are just to facilitate the explanation.
|
|
Column 1 |
Column 2 |
|
Row 1 |
|
|
|
Row 2 |
Angle A |
log 1 – log sine A |
|
Row 3 |
Angle B |
log sine B |
|
Row 4 |
Angle C |
log sine C |
|
Row 5 |
Side A (known side) |
log a |
|
Row 6 |
Unknown Side B |
Sum logs Rows 2+4+5 |
|
Row 7 |
Unknown Side C |
Sum logs Rows 2+3+5 |
By writing the value for log sine A on the line above (Col.2,Row1) the angle A value, the value for log 1 – log sine A could be written in that space (Col.2,Row2). Thus the four logarithmic values needed to complete the two side calculations were now sequentially listed. The requisite three of the four logarithmic values were then added to obtain the side value. An American description of this layout and its practical operation suggested convenient templates can be cut out of heavy paper to facilitate this [the addition of the applicable rows to complete Rows 6 and 7 in turn] operation.
The following is from Calculations Book 6A for the Triangulation Survey of South Australia 1878-1882 under Trigonometrical Surveyor William Henry Cornish (1850-1888) of the South Australian Survey Department. The completely handwritten, pen and ink sketches, tabulations and computations appear to be the work of Charles Hope Harris (1846-1915) the Survey Department’s Chief Computing Officer at the time. A sample of the dual page layout from the Calculations Book may be viewed via this link. The triangle and its associated calculations have been numbered (bold) for reference. It should be noted that as the triangle sides were only of some 10-15 miles no spherical excess was applied; for brevity, degree, minute and second symbols were replaced by dots and spatial separation.
Systematically all the angles and distances throughout the triangulation were determined. These data would then permit the calculation of geographical coordinates for each triangle vertex once the mathematical shape of the curved surface was agreed.
Adoption of a Spheroid
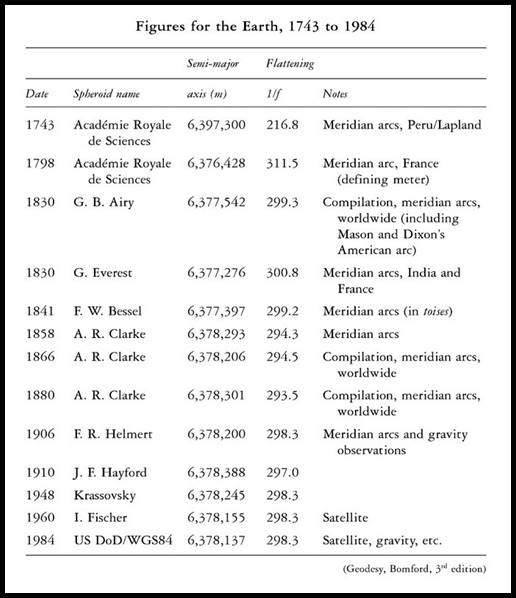
From various, generally triangulation surveys, mainly in the northern hemisphere, data were analysed to determine the best mathematical representation of a figure for the Earth. A list of some of these results is shown below. Today, Global Reference System (GRS80) is the accepted figure for the Earth with its parameters differing from the WGS84 parameters quoted below by only a few decimal places. The parameters which defined a spheroid were historically known by their founder and date. Bessel 1841 and Clarke 1858 are two of the most common. Australia used Clarke’s 1858 figure until it was replaced in 1966 with the Australian National Spheroid (equatorial semi axis a= 6 378 160 meters and 1/f= 298.25).
The acceptance of the spheroid as the mathematical working surface, required that formulae be established permitting survey data observed in the field to be firstly converted to geographical coordinates (latitude and longitude) and later defined map grid coordinates. The survey data would be in the form of azimuths (direction from north) and distances between points in the terrain.
Two sets of formulae were then required :
|
- |
Forward method : |
from a point with known (or assumed) geographical coordinates using the azimuth and distance to a second point, calculate the geographical coordinates of this second point along with the reverse azimuth, as on the spheroid azimuths are not exactly 180 degrees different; and |
|
- |
Reverse or Inverse method : |
knowing the geographical coordinates of two points, calculate the distance between them and the forward and reverse azimuth from one to the other point. |
Of the formulae developed, it was those of Louis Puissant (1769-1843), Professor of Mathematics at the Military Academy at Fontainebleau, France, and published in his 1805 work Traite de Geodesie, that were mostly accepted and utilised until electronic calculation became common place.
Some of the other formulae developed, including Puissant’s (Clark, 1966), were :
|
Name |
Use and accuracy |
|
Bessel’s formulae (Friedrich Wilhelm Bessel (1784-1846) Director and Professor of Astronomy at the then Königsberg (Kaliningrad, Russia) observatory) |
Developed and showed an example of formulae in 1825. |
|
Clarke’s (Clark, 1966) formulae for long lines (Alexander Ross Clarke (1828–1914) was responsible for the principal triangulation of the British Isles and published the results of the first geodetic survey of Great Britain in 1861) |
Ordnance Survey, UK, and US Coast and Geodetic Survey used for the longest lines visually possible from ground stations said to be 200 miles or 300 kilometres. Hume F Rainsford added extra terms to the formulae to make them useful over distances of 500 miles or 800 kilometres to 1 part per million (1 mm per 1 km). |
|
Clarke’s formulae for medium-short lines (Clarke, as above) |
Mainly by Ordnance Survey, UK, for lines up to 70 miles or 100 kilometres. Ignored some of the smaller terms of the long line formulae. |
|
Mid Latitude formulae (various) |
Less accurate than above but could be used over distances up to 25 miles or 40 kilometres in the latitudes between the equator and 60 degrees, without introducing errors greater than 0.01 seconds of arc. |
|
Puissant’s formulae (Louis Puissant (1769-1843)) |
In India and USA over distances to 80 miles or 120 kilometres, Puissant's formulae were accepted to be accurate to 1 part per million (1 mm per 1 km). The Australian adaption in 1972 was quoted as accurate to 1 part per million over distances up to 80 kilometres or 50 miles. |
|
Puissant’s simplified formulae (Puissant, as above) |
US Coast and Geodetic Survey as well as Australia used these formulae over distances up to 40 kilometres with an accuracy of about 0·3 metres in position and about 1 second of arc in azimuth. |
|
Sodano technique for long lines (Emanuel Michael Sodano (1919-2010) worked at the US Army Map Service and the Army Geodesy, Intelligence and Mapping Research and Development Agency) |
Extensively during airborne electronic distance measuring HIRAN operations by the US Army Map Service, azimuth data obtained during LOLA (LOng Line Azimuth) line crossings were processed using the SODANO technique to solve for the reciprocal azimuths from the two stations. A rigorous and non-iterative inverse solution of very long geodesics for computation by desk calculators, it required no special tables and was accurate to the tenth decimal place of radians for the azimuths and distance or less than 0.01 seconds of arc and less than 1 metre in distance for distances to 350 miles or 550 kilometres. |
|
Robbin’s for long lines (Alwyn R Robbins (1920-2002) became Reader and Head of the Department of Surveying and Geodesy, Oxford) |
Introduced in 1962 these formulae were accurate to better than 20 millimetres over distances of 1 500 kilometres. Errors could reach 16 metres at 4 500 kilometres, and more than 2 000 metres at 9 000 kilometres. It was not foreseen that these formulae would ever be used for hand computation. |
Puissant showed that at a distance of s metres and azimuth A from a point the difference in latitude and longitude and reverse azimuth, in radians, could be found by :
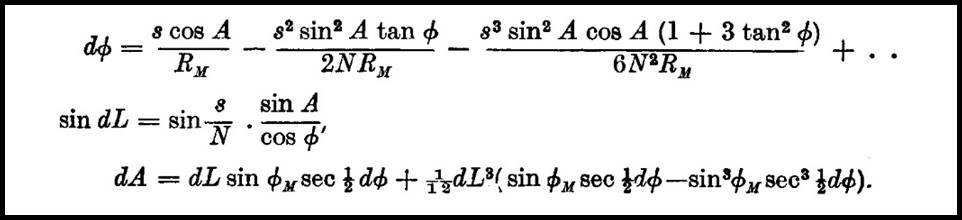
where from the parameters of the selected spheroid, a being the equatorial semi axis and b the polar semi axis :
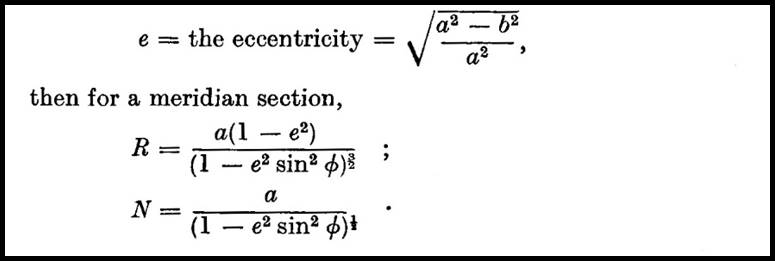
To reduce computational effort and errors, tables were constructed for R and N, radii of curvature of the spheroid in the meridian and prime vertical respectively, and their combinations (see CONSTANTS below) for the latitudes of the survey area. Such tables would have been produced as logarithms to further reduce computational effort.
As early as 1846, Puissant’s formulae had been adapted for use by the US Coast and Geodetic Survey. At this time, the Americans were only a few years into their national triangulation survey. The associated tables, discussed below, were first computed in 1847, and were used in manuscript form up to 1860, and at later dates they were extended in range of latitude in order to satisfy the further demands of the survey. The initial tables were based on Bessel’s 1841 spheroid before changing to the Clarke 1866 in 1880. The fourth edition of Formulae and Tables for the Computation of Geodetic Positions was published as Appendix No.9 to the Coast and Geodetic Survey report, Progress of the Work for Year Ending June 1894. By now the tables had been expanded to encompass the latitudes from the Equator to 72° north. In 1911, the Coast and Geodetic Survey published their fifth edition of Formulae and Tables for the Computation of Geodetic Positions, as a standalone Special Publication No.8. In its introduction it was mentioned that a significant driver behind this fifth edition was that the supply of the fourth edition was exhausted. As can be seen below the tables were still being produced as logarithms. After the commencement of World War 11 the tables were published under the US Army TM (Technical Manual) designation. Following the establishment of the Australian National Spheroid in 1966 appropriate tables were printed by the US Army TM 5-241-33. With permission these tables were reprinted in 1972 by the National Mapping Council as The Australian Map Grid : Latitude functions for the Australian National Spheroid, Special Publication 7C. With hand operated machine calculation being introduced the tables were no longer produced as logarithms.
In addition to tables for the spheroids of Bessel - TM 5-241-19, Clarke 1866 - TM 5-241-18 and the ANS - TM 5–241-33, similar tables were produced over time for the Hayford (International) - TM 5-241-17, Everest - TM 5-241-21 and Clarke 1880 - TM 5-241-20, spheroids.
The American adaption of Puissant’s formulae was :

for use with the following tables of constants :

When adopted in Australia and published in 1972 by the National Mapping Council in, The Australian Map Grid – Technical Manual, Special Publication 7, Puissant’s formulae had been adapted further as follows, where subscripts 1 and 2 indicated the value of the known and unknown points respectively and subscript m indicated that the mean value be used :

Puissant’s formulae were thus easily adapted to a proforma layout at a time when Australian survey lines seldom exceeded 100 kilometres in length due to terrain height, visibility over such a distance and later the limitations of electronic distance measuring devices. The occasional line of longer length could be handled with other formulae.
Today, the formulae of Thaddeus Vincenty (born Tadeusz Szpila; 1920-2002), published in 1975 and stated to be accurate to about half a millimetre over any distance are freely available for any type of computation. Vincenty’s formulae used an iterative method to achieve the required accuracy and could be used with any spheroid over any distance.
Sources
Bessel, Friedrich Wilhelm (1837), Determination of the Axes of the Elliptic Spheroid of Revolution which most nearly corresponds with the existing Measurements of Arcs of the Meridian, Article XII, Astronomische Nachrichten (Astronomical Notes), No.333, as found in Taylor Richard (1841), Scientific Memoirs, Selected from the Transactions of Foreign Academies of Science and Learned Societies and from Foreign Journals, pp.387-400, as accessed from : https://books.google.com.au/books?id=Nn9HAQAAMAAJ&pg=PA601&lpg=PA601&dq=Bessel+Determination+of+the+Axes+of+the+Elliptic+Spheroid+of+Revolution&source=bl&ots=twjIBCXC9v&sig=ACfU3U2zdZKeLe8joNxrqYeVTVNb-EoFdw&hl=en&sa=X&ved=2ahUKEwi6vsT8sPThAhVOfisKHQTMB4UQ6AEwBHoECAkQAQ#v=onepage&q=Bessel%20Determination%20of%20the%20Axes%20of%20the%20Elliptic%20Spheroid%20of%20Revolution&f=false
Bessel, Friedrich Wilhelm; Karney, Charles, FF and Deakin, Rodney E (2012), The calculation of longitude and latitude from geodesic measurements, an English translation of FW Bessel, Astronomische Nachrichten 4(86), 241-254 (1825), accessed at : https://arxiv.org/pdf/0908.1824.pdf
Bomford, Guy (1971), Geodesy, (Third Edn), Oxford Press, London.
Clark, David (1966), Plane and Geodetic Surveying for Engineers, Vol.2, Constable & Co. Ltd, London.
Coast and Geodetic Survey (1894), Progress of the Work for Year Ending June 1894, Part ll, Appendix No.9, pp.277-348.
Coast and Geodetic Survey (1911), Formulae and Tables for the Computation of Geodetic Positions, Special Publication No.8 (5th Edn.), Government Printing Office, Washington, accessed at : https://tile.loc.gov/storage-services/public/gdcmassbookdig/geodesyformultab00unit/geodesyformultab00unit.pdf
National Mapping Council (1972), The Australian Map Grid – Technical Manual, Special Publication 7.
Puissant, Louis (1805), Traite de Geodesie, Libraire pour les Mathématiques, Paris, accessed at : https://books.google.com.au/books/about/Trait%C3%A9_de_g%C3%A9od%C3%A9sie.html?id=PcAJAAAAMAAJ&redir_esc=y
Rainsford, Hume F (1955), Long Geodesics on the Ellipsoid, Bulletin Geodesique, No.37, pp.12-21.
Rainsford’s Formulae for Long Geodesics
(after : Rainsford, Hume F (1955), Long Geodesics on the Ellipsoid, Bulletin Geodesique, No.37, pp.12-21.)
|
Formulae |
|
|
Examples |
|

