DIVISION
OF NATIONAL MAPPING
DEPARTMENT OF MINERALS AND ENERGY
Training
Notes for National Mapping Field Survey Staff
Compiled
by RA (Reg) Ford 1974
CONTENTS
1. CHAINING
AND LEVELLING.
1.1. Chaining.
1.2. Use of the plumbob.
1.3. Care of the tape.
1.4. Step chaining.
1.5. Slope chaining.
1.6. The Abney Level.
1.7. Errors in chaining.
1.8. Use of the spring balance & thermometer.
1.9. Clearing of lines for chaining.
1.10. Reading the chain.
1.11. Third order traversing with chain and theodolite.
1.12. Accuracy standard of third order traversing.
1.13. Marking the traverse.
1.14. Location of the traverse.
1.15. The traversing party.
1.16. Distance between stations.
1.17. Pickets and targets.
1.18. Field chaining.
1.19. Odd lengths in field chaining.
1.20. Corrections to chained distances.
1.21. Summary of chaining corrections and errors.
1.22. Algebraic signs of errors.
1.23. Errors of a full chain length.
1.24. Check measurements.
1.25. Angular measurements.
1.26. The Surveyors' Level.
The
Tilting Level.
The Automatic Level
The Level tripod.
The Levelling Staff.
Testing and adjusting the level.
1.27. Level Traversing - Hints.
Extracts from "Specifications,
Third Order Levelling."
Field Book - Rise and Fall Method.
Field Book - Collimation Method.
2. THEODOLITE,
GENERAL DESCRIPTION, ITS USE IN ALL TYPES OF OBSERVATIONS.
2.1. General Description.
3. THEODOLITE,
WILD T2, OBSERVING METHODS, TASKS AT TRAVERSE STATIONS.
3.1. General preparations includes T2 manual.
3.2. Setting up, screens, levelling, etc.
3.3. Horizontal and vertical scales, description and reading.
3.4. Observing horizontal and vertical angles, double pointing system,
scale settings, and booking.
3.5. Measuring and recording RM's, Eccentric Stations, Recovery Marks,
Computation of RM distances.
3.6. Eccentric corrections, all types. Formula, computations &
example.
3.7. Plumbing towers and beacons, with theodolites.
3.8. Sigma Octantis azimuth determinations, method and booking.
3.9. Hints on Ex-Meridian sun azimuth determinations, method and
booking.
3.10. Meridian transit observation for Latitgde and Longitude,
Rimington's Method.
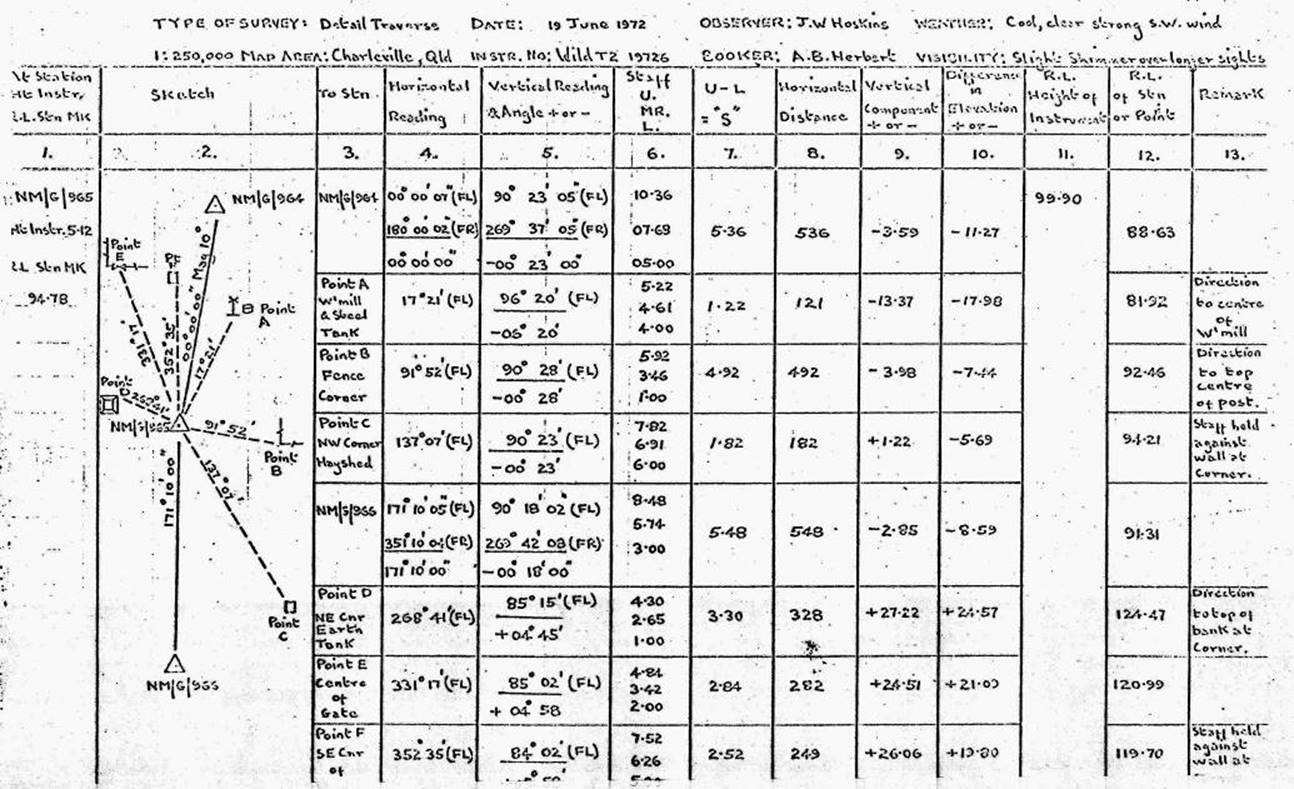
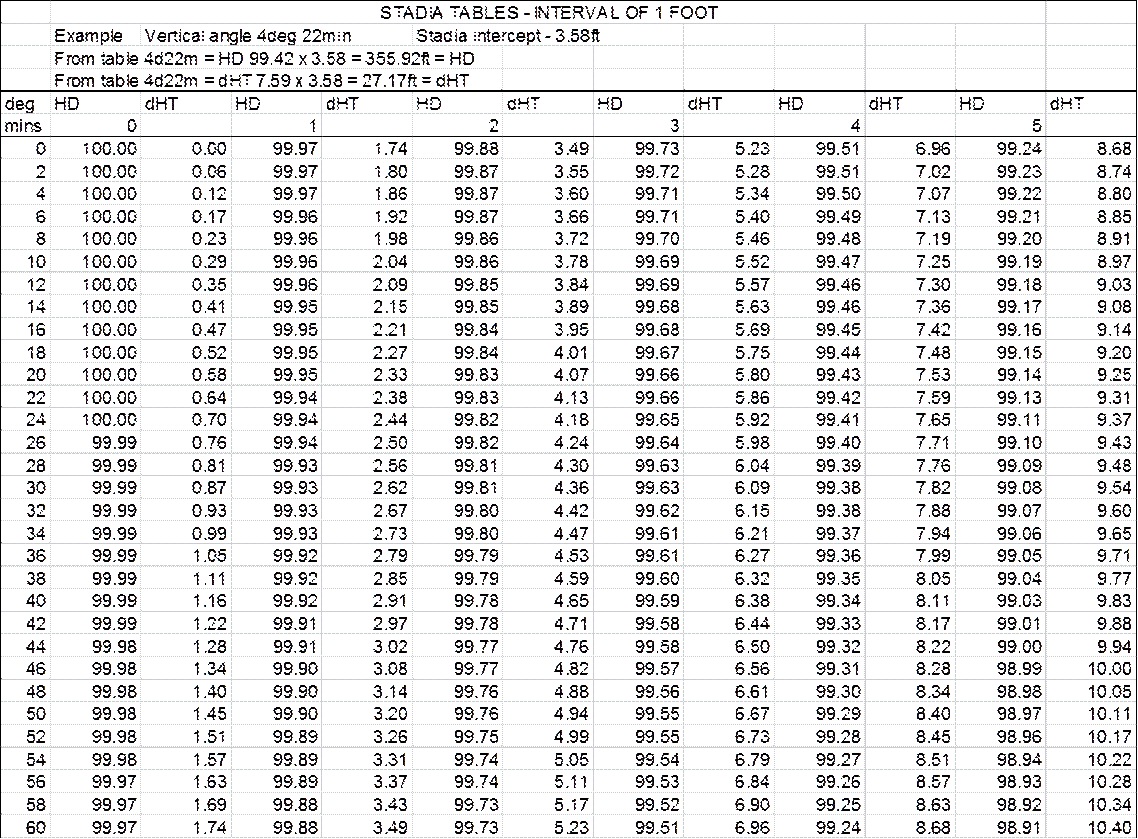
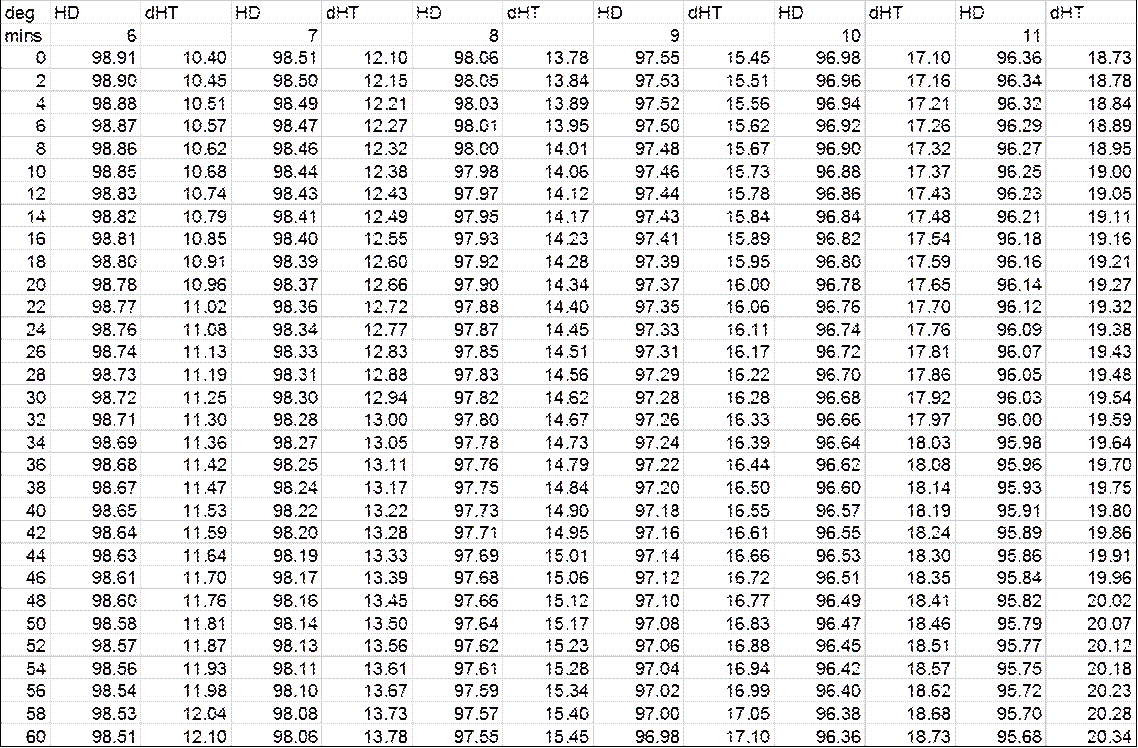
3.11. Tacheometry, or Stadia Surveying.
Theory.
Reduction of stadia observations.
A tacheometric traverse to gather
detail.
Field Book - layout and finalization.
Stadia Tables.
Accuracy - distance and heighting.
Curvature and refraction.
3.12 Almucantar observation for Longitude
with Wild T3 Theodolite and stopwatch.
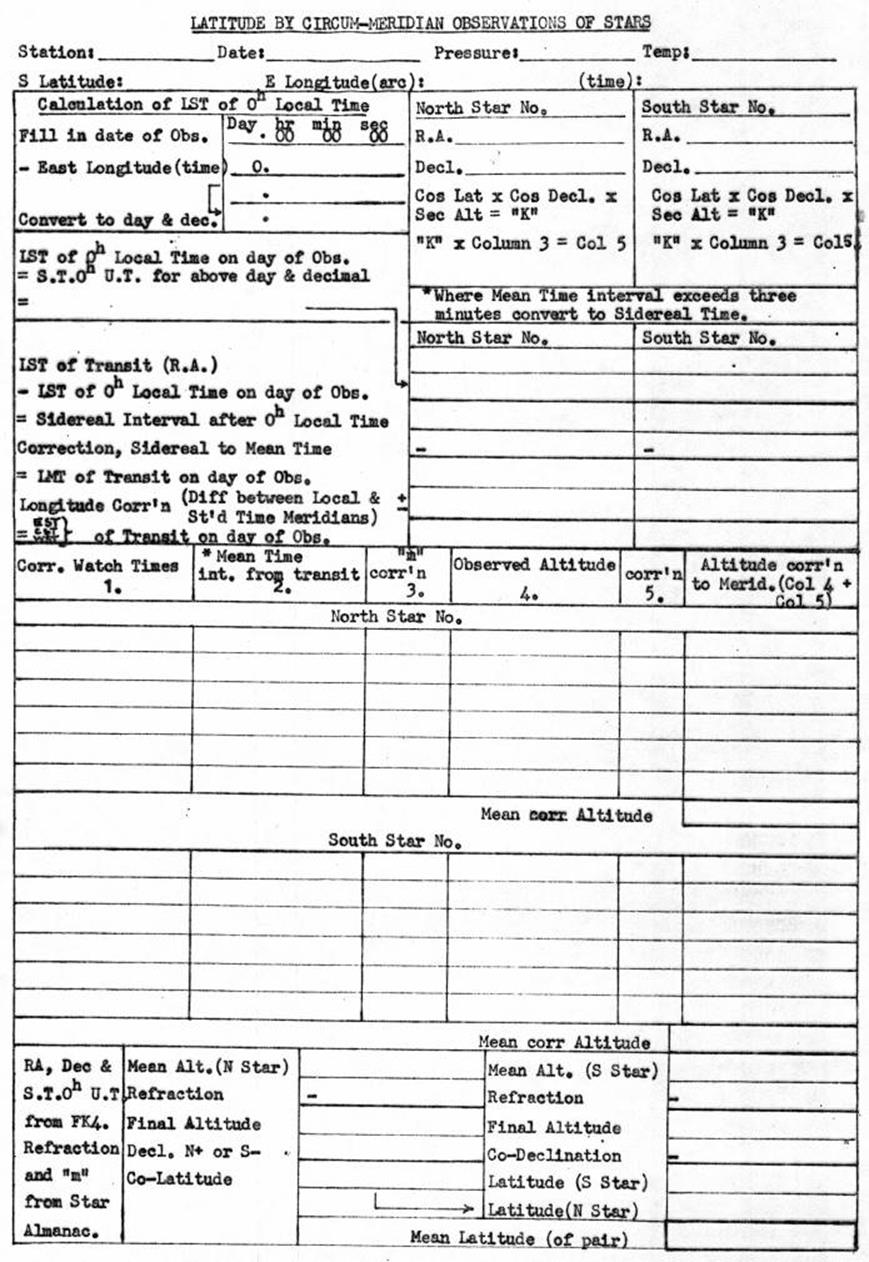
3.13 Latitude
observations with the Wild T3 Theodolite – Meridian or Circum-Meridian
Altitudes.
4. TELLUROMETER,
MRA2.
4.0. Setting up.
4.1. Description of the operating panel.
Use of the controls.
Pre-operational checking.
4.2. Operation under usual conditions.
Pattern of operation.
Sequence of measuring.
Operation over land.
Operation over water.
Atmospheric effects.
4.3. Field computation of the measurement.
Atmospheric readings required.
Explanation of the "Coarse"
figure.
Simple explanation of the tellurometer
system.
Field book example of the computation.
4.4. Fault finding procedure.
Faults common to the
Master and Remote instruments.
Faults peculiar to the
Master instrument.
Faults peculiar to the Remote instrument.
Anomalous CRT displays.
Trouble shooting charts.
4.5. TELLUROMETER, MRA3.
General principles
Simplified theory of measurement
Conversion of time to distance
Zero error
The control panel
Dial readout unit
Making contact, preliminary
arrangements
Sequential method of operation
4.6. TELLUROMETER, MRA4 – MANUAL.
5. THE COMPASS.
How to read the prismatic compass.
Magnetic declination.
Compass error.
Protracting bearings from maps.
6. MIRRORS AND HELIOGRAPHS.
Use of the mirror for proving
intervisibility.
Description of the heliograph.
Setting up the helio for
"Simpler," operation.
Setting up the helio for
"Duplex" operation.
7. STATION MARKS AND
MARKING.
Description of types of station marks.
Standard mark for one degree and half
degree Control Stations.
Reference Marks, Witness Posts, etc.
Types of marks previously used.
How to build cairns.
Tripod and quadrupod beacons.
8. ERECTION OF TOWERS AND MILLS SCAFFOLDING OBSERVING PLATFORMS.
8.1. Stand
point for the tower; dimensions of concrete blocks.
Assembling and erecting the tower.
List of tower parts.
8.2. Necessary
tower attachments.
8.3. Erecting
the Mills scaffolding observing platform.
Sequence of erection.
List of parts required. Weight of one
complete scaffolding.
9. ACCESS NOTES AND SKETCHES.
9.1. General.
9.2. Field
notes of the speedo and compass traverse.
9.3. Drawing
the access sketch; conventional signs.
9.4. Helicopter
access.
10. MAP READING INCLUDING ELEMENTARY AERIAL NAVIGATION, USE OF THE
PLANE TABLE.
10.1. Objects
of Map Reading.
10.2. Understanding
maps.
Marginal information.
Mapping
terms.
True, Magnetic & Grid bearings.
Protracting bearings.
Scales, Map Symbols, Relief &
Contours.
Australian Map Grids. Use and reading
Grid (Map) References.
10.3. Hints
on Map Reading.
10.4. Elementary
Aerial Navigation.
10.5. The
use of the Plane Table.
11. ELEMENTARY
ALGEBRA, LOGARITHMS, PLANE GEOMETRY & TRIGONOMETRY
Algebra, Logarithms, Plane
Geometry and Trigonometry.
12. SURVEY
COMPUTATIONS.
12.1 Closed Surveys (Chain & Theodolite traverses).
Bearings, Latitudes & Departures.
Misclosures, computing the closed traverse.
Computing missing bearings and
distances.
Use of Eastings & Northings
instead of Latitudes & Departures.
12.2. Spherical Excess & closure of triangles.
Formulae, figures used in
triangulation.
Calculation of sides, spherical
excess. Triangle miscloures.
12.3 Field computation, Latitude, Longitude & Reverse Azimuth.
Definitions and formulae.
Sequence of computation.
Tables used; example of computation.
12.4. Heights from Simultaneous Reciprocal Vertical Angles.
Obtaining the Curvature and Refractive
(C&R) index from Single Ray Vertical angles.
Applying the Curvature and Refractive
(C&R) index to single ray vertical angles.
12.5. Astronomical Terms used in Observations and Computations.
12.6. Time and Time conversions, Hour angle.
12.7. Computation of Ex-Meridian Sun Observation for Azimuth.
12.8. Computation of Azimuth from a close circum-polar star.
Plate bubble corrections in Azimuth
observations.
Interpolation of Right Ascencion and
Declination of Sigma Octantis.
Time curvature correction between FL
& FR pointings.
12.9. Barometric heighting with Mechanism Barometers (Field
computation).
Examples of various machine computations
and Table of Temperature Constants.
Examples of computation using Log
formula,
Table of Temperature Constants for use
with Log formula.
12.10. Computation, meridian transit observation for Latitude and
Longitude, Rimington's method.
12.11 Almucantar observation for Longitude computation.
12.12 Latitude by Circum-Meridian Altitudes computation.
______________________________________________________________
1 Chaining
1.1.1
The direct measurement
of distance with a steel band is referred to as "chaining”, from the use
of the original Günter’s chain of 100 links. Modern steel bands are generally
about 3.18mm wide and 0.25mm thick. The length now being used within the Division
is 50 metres. The bands are graduated with stamped brass rivets or sleeves.
1.2 Plumbob
1.2.1 This is used for testing
the verticality of beacon poles, transferring to ground the end marks of steel
bands, setting the theodolite over fixed points and step chaining.
1.2.2 To hold the plumbob cord on
the tape, the cord and tape are pinched together by the thumb and forefinger,
at the points shown by the arrows in Figure 1.2.2.
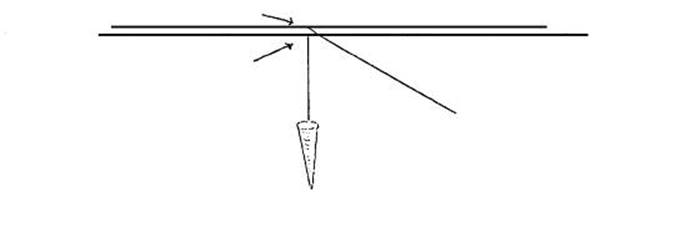
Figure 1.2.2.
1.2.3 The two extreme positions
likely to be encountered when using the plumbob to transfer the position on the
tape to a ground point, or vice versa, are:-
(a)
shoulder height.
This is the limit without losing accuracy;
(b) peg height.
1.2.4 When using the plumbob,
there will be slight movement of the bob, due to vibrations from the tape,
wind, etc. This movement can be reduced to a minimum by gently tapping the ground
with the point of the plumbob.
1.2.5 When the line of sight from
the theodolite to a point is obstructed, it is possible to use the plumbob as a
target. In order to minimise the error due to the movement of the plumbob, the
string should be held as close as possible to the top of the plumbob. The point
of the plumbob should be kept as close as possible to the point being plumbed.
The correct method of holding the plumbob is shown in Figure 1.2.5.
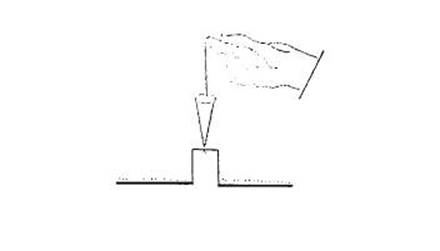
Figure 1.2.5.
1.2.6 In order to mark a point
with the plumbob, the tip of the bob should be about 13mm above the ground, and
when the order to mark is given, the assistant settles the plumbob and a
clearly defined hole is made with the point. If the ground is too hard for the
point to mark, the plumbob is kept in the position shown in Fig. 1.2.6 until a
chaining arrow is inserted.
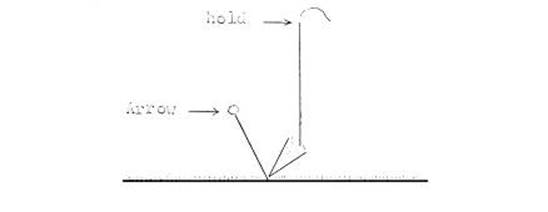
Figure 1.2.6.
1.3 Care of the tape
1.3.1 When unrolling the band, 1
assistant takes the free end of the tape and walks slowly forward, while the
other assistant holds the arrow on which the cross revolves, or the strap of
the reel, so that the band comes off freely and easily, without jerks. The man
at the cross or reel end also sees that the band does come off too quickly, and
that it does not get caught on obstacles. As his end of the band comes in
sight, he warns the man at the other end to be prepared to stop, at, the same
time preparing to give a little at his end, in case of a sudden jerk. When the
end of the band is reached, he gives the signal to stop, and both men lay the
ends of the band on the ground, ready to start work.
1.3.2 In rolling up, the band is
first laid out straight on the ground and one end is fastened to the cross or
reel. The man working the latter, now starts to walk slowly towards the other end
of the band, at the same time winding it up. In doing this he sees that it is
not caught on any obstruction and is wound firmly and tightly without any
sudden jerks taking place. When the end is reached, it is fastened to the cross
or reel by means of a strap or leather lace.
Although most steel tapes used for surveying
will withstand a direct tension of 36 Kilograms (about 80 lbs.) it is very easy
to break them by misuse.
When a tape is allowed to lie on the
ground, unless it is kept extended so that there is no slack it has a tendency
to form small loops like that shown in Fig. 1.3.3. When tension is later
applied, the loops become smaller either it jumps out straight or the tape
breaks, as shown. If a tuft of grass or any object is caught by the loop, the
tape almost always breaks or at least develops a permanent "kink". To
avoid this, the tape must be handled so that no slack can occur. For
measurements of less than a full tape length, the tape should be kept on the
reel. It should be reeled out to the necessary length, and reeled in as soon as
possible. The assistant, who handles the reel, must reel in any slack that
might occur between the two assistants, while the tape is being handled. For
measurements greater than the tape length, when the tape is off the reel, the
tape should be kept fully extended in a straight line along the direction of
measurements. When it is to be moved, it must be dragged from one end only.

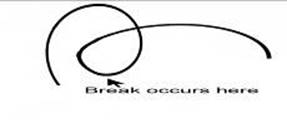
Figure 1.3.3.
If
it is necessary to raise the tape off the ground, the two assistants must lift
the tape simultaneously and keep it in tension between them. Except for this
operation, the rear assistant must not touch the tape while it is being moved.
If he picks up the rear end, and moves forward faster than the other assistant
le will form a "U" in the tape, which usually causes a loop to form
when the tape is pulled taut. This may break the tape.
1.3.4 When the end of the
measurement is reached, where a less-than-tape-length measurement is required,
the assistant must not pull in the tape hand over hand as this creates a pile
of loose tape on the ground. Instead, he must do one of three things:-
(i)
Carry the end of
the tape, beyond the point, lay it on the ground, and walk back.
(ii) Reel in the tape, the requisite
amount.
(iii) Take in the tape, forming figure-eight
loops hanging from the hand. Each length of tape must be laid in the hand flat
on the previous length and never allowed to change. Later, to extend the tape,
lay it out carefully as he walks forward, by releasing one loop at a time. This
method requires care and practise and should not be attempted until the
required skill has been obtained by practise.
1.3.5 No vehicle should be
allowed to run over the tape. Only in the case where the tape is across a
smoothly paved street can a pneumatic tyred vehicle pass over the tape without
damaging it. The tape must be held flat, and tightly pressed against the street
surface by the two assistants.
1.3.6 When a tape is wet, it should
be carefully cleaned, one oiled immediately after use.
1.3.7 In general, it is well to
remember that a tape is easily damaged but, with care and thought, damage
seldom occurs, keeping the following in mind:-
(a)
Keep the chain
straight. If, for any reason it is necessary to pull it back do so from the end,
rather than let it lie in a series of loops at an intermediate point from which
it is pulled.
(b)
If pulling the
chain around a corner see that it is pulled around a curve of large radius, and
have an assistant watching it to see that the sleeves do not catch in a
splinter or a piece of barbed wire or anything else which might break the chain.
(c)
If the chain is
caught do not attempt to free it by jerking but go back and release it where it
happens to be caught.
(d)
In running out a
Box Tape from its case see that it runs out tangentially and is not bent back
where it leaves the case. The tape should always be kept bright and clean.
If
it gets wet, dry it at once, and if it becomes muddy, wash the mud away with
clean water then dry the tape. It should never be wound up into the case when
wet, but while drying it should be hung in a series of wide loops, which will
allow it to dry quickly.
If
it becomes dirty or rusty it should cleaned with kerosene, oil, or some non-abrasive
such as "Brasso".
1.4 Step chaining
1.4.1 Measurements are carried
forward by holding the tape in a horizontal position, and the plumb line is
used by either or at times, by both assistants for projecting from tape to
ground. Figure 1.4.1. shows an example of "Step chaining".
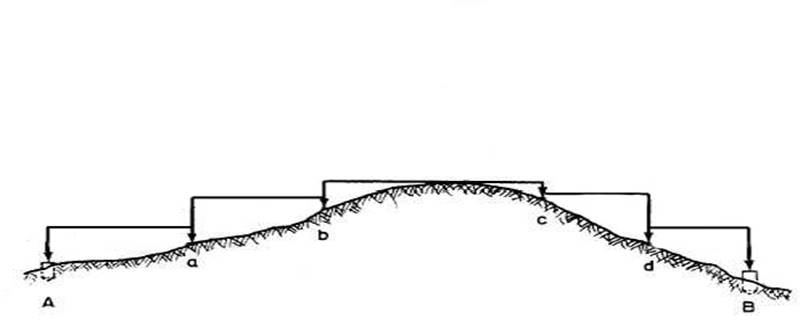
Figure 1.4.1.
1.4.2 It requires some practise
to judge when the tape is horizontal. The best way is to pull sufficiently to
eliminate sag and hold the stretched tape so that the angle between it and the
plumb line is a right angle. It is impossible to judge horizontality from the
uphill end of the tape.
1.4.3 In step chaining the length
of the step will depend upon the angle of slope, and should not be so long that
the height of the plumbed end above the ground exceeds 1.5 metres.
1.4.4 It should be noted that
holding one end of a 50metre tape 1 metre above or below the true horizontal
line will cause an error in the result of 8mm. Hence the need for a very close
approximation to the level line, at the instant of plumbing.
1.5 Slope Chaining
1.5.1 The tape is held on a slope
and the angle of slope read so that the measurements can be reduced to the
horizontal.
1.5.2 The chain may be held at
any convenient height at both ends however it is usual practise to hold waist
high, the rear assistant reading the slope.
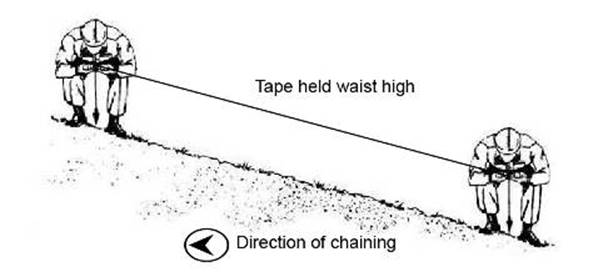
1.5.3 For slopes up to 4° the
Abney Level (See 1.6.) is used to read the angle of slope. For slopes above 4°
a theodolite should be used to read the vertical or slope angle. The theodolite
is set accurately over the chained point, and the angle of slope read, to the
assistants hand as he releases the plumbob at the "mark" signal.
1.6 The Abney Level
1.6.1 This is one of the popular
instruments of the surveyor's kit. It is not a precise instrument by any means,
angles of slope are read to within two minutes, in the larger size, and to within
ten minutes in the smaller size. There is no magnification in the sighting tube
through which the bubble and target are viewed at the one time. Below is shown,
the method of using the Abney Level for chaining. A 4° slope is being read
which is the allowable limit for the Abney Level.
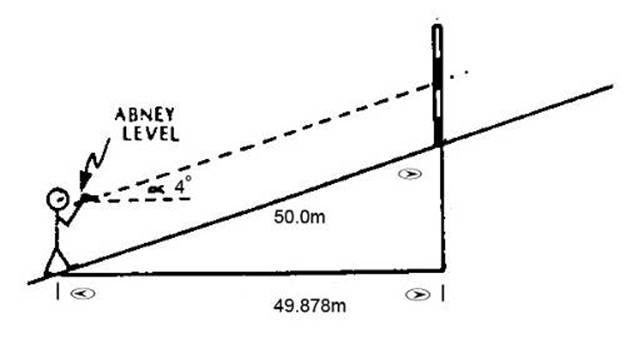
Figure 1.6.1(a)
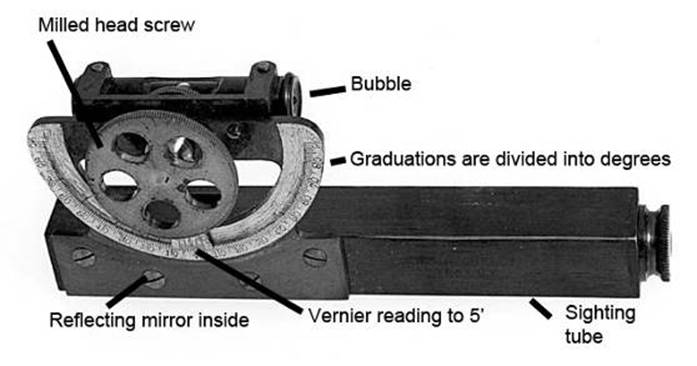
Figure 1.6.1(b)

Figure 1.6.1(c)
The
graduated circle is divided into degrees, and the vernier to read to 5 minutes
= 11 divisions of graduated circle divided into 12. Reading either side of
index to 5¢.
1.6.2 Adjustment
of the Abney Level
By
taking the mean of back & fore sights. Two points of different elevation
are selected, and the vertical angle between them is observed from both.
The
angle of elevation observed from the lower station should equal the angle of depression
from the higher. If not, the mean is the correct reading and the instrument is
made to record this by the adjusting screws on the level.
Alternative to (b), the index error can
be used :-
If
the reciprocal observation gives 15° elevation and 17° depression, the index
error is half the difference, i.e. 1° to be deducted from all depression
angles and added to all elevation angles.
The following is probably a better
method of recording and using, an Abney Level correction:-
With
a theodolite determine the altitude of a well defined object some 500 metres
away. Set this angle on the Abney Level, sight on the object with the Abney
Level. Observe, carefully, where the sighting mark "cuts" the bubble
reflection. It may be half or quarter way down from the top, etc. In future
determinations of slope bring the bubble to this same position, relative to the
sighting mark. When continuous use of the Abney Level is being made, it should
be tested, as described, every 2 or 3-days.
1.7 Errors in chaining
1.7.1 Even experienced assistants
have difficulty in preventing the tape and the plumbobs from moving, during
measurements. The error from this source is, between 1:5,000 and 1:10,000.
Variations in tension of 2.27kilogrammes (about 5 lb) introduce an error of
1:10,000 with a tape of average cross section, 50 metres long, and supported at
the ends. Temperature may introduce an error of up to 1:5,000 so that, all in
all, this type of measurement has an accuracy seldom better than 1:2,500. Using
spring balance handles will improve the accuracy to 1:3,000. With temperature
correction, as well, an accuracy of 1:5,000 can be attained.
1.7.2 If
more accurate results are required then special equipment is necessary.
1.7.3 A distinction should be made
between errors and blunders. Errors result from such things as:-
Incorrect alignment of the chain.
Temperature variations.
Tension variations.
Tape
not straight.
Blunders are usually due to:-.
Miscounting of chain lengths.
Misreading the chain.
Erroneous booking.
Misplacement of a chainage point.
1.8 Use of Spring Balance and Thermometer
1.8.1 It should be noted that a
50 metre tape will expand or contract 1mm for every 2°C change in temperature,
or 8mm for every 15° C. It is very difficult to read an exact
temperature of the tape.
In general, the thermometer should be
held as close to the tape as possible, while taping is taking place. The ideal
situation would be to have the thermometer clipped onto the band, with the bulb
in contact with the steel.
1.8.2 The spring balance is
simply attached to one and of the band and tension is applied, until the tension,
at which the tape has been standardised, is reached. This is generally about
3.630 kilograms (about 8 lb) to 4.600 kilograms (about 10 lbs), when using the 50
metre band for chaining.
Tension
should not be applied quickly, but as a gentle pull, applied by the leading
assistant; this will reduce jerking, etc.
1.9 Clearing lines for chaining
1.9.1 Prior to commencing
chaining, the line should be cleared of all obstacles which may tangle or bend
the tape. Grass, scrub and trees, should be cut down as low as possible, and
where chaining is to take place, with the tape resting on the ground, the line should
be scraped free of all vegetation, rocks, etc. The principal problem in
clearing vegetation from a survey line is maintaining a straight line.
If this is done, the effort involved
is kept to a minimum, and work progresses more rapidly and systematically.
Quite often, large trees have been felled only to find later that they were
well off line. It is far better to take some trouble to locate the correct
line. This is best done by using "sighting sticks" or "boning rods".
The first stick is set on the required
line by theodolite or compass, at some convenient distance from the station. The
axeman can then walk "on line" by looking back and aligning himself
with this stick, and the theodolite. Before he loses sight of the back mark, in
this case, the theodolite, the axeman should cut another bush stick, an inch or
so, in diameter, driving it into the ground, on line with the previous marks.
He then maintains direction by aligning himself with the two closest marks.
This process is carried on for as far as necessary. Shorter sticks are used
when clearing over a ridge; and longer ones when crossing a depression. If
carefully executed, straight lines can be maintained for considerable
distances, say about 1 kilometre, with an error of about half a metre,
depending on the terrain.
1.10 Reading the chain
1.10.1 Steel bands, now in use in
the Division of National Mapping comprise a 50 metre steel section, marked with
brass studs each metre. Attached to the zero end of the band is a leader 1 metre
plus long. The leader is graduated to millimetres.
1.10.2 In order to measure an
uneven distance, the leader is held roughly over the forward station, by the forward
assistant. The rear assistant then holds the nearest graduation on the band
over the previous chainage mark. At the "read' signal
given
by the rear assistant, the reading on the "leader"
is noted by the forward assistant, and the rear assistant reads, the whole
metre on the band. To minimise the possibility of misreading, the two
assistants now change position, and the procedure is repeated. See Figure
1.10.2.
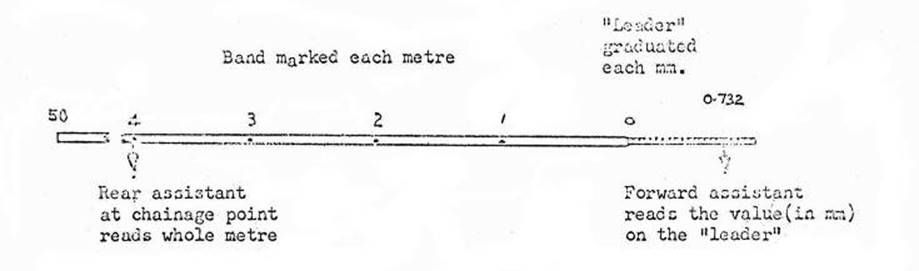
Figure 1.10.2.
Rear assistant reads 04.000
metres.
Forward assistant reads 0.732 "
Distance 04.732
metres
1.11 Third Order Traversing
1.11.1 Theodolite
and chain traverse
This
is the method by which cadastral survey work is carried out, and boundaries of
properties, measured and marked, or re-established, on the ground.
In
mapping, 1st and 2nd order traverses are now carried out with electronic
distance measuring equipment, taking the place of the chain. However, there is
still a need for traversing of 3rd or 4th order standard. The latter is often a
short connection to a photo reference point, etc., where a spring balance and
accurate slope corrections are a needless refinement.
It
is envisaged that traversing similar to the third order traverses would be
required to connect mapping control points to distant satellite stations, or
short traverses to get mapping control into timbered flat, terrain, unsuitable
for electronic measuring equipment.
1.12 Accuracy Standards for Third Order Traversing
1.12.1 Error
between traverse control points and adjacent control
The
traverse control points should be determined with sufficient accuracy so that,
after adjustment, it will be unlikely that the computed distance between a 3rd
order control point and any adjacent 3rd or higher order, control point, will
be in error by more than 1 part in 5,000.
1.12.2 Errors
of standardisation, and between adjoining stations of the traverse.
The
probable error of standardisation of the field tape should not exceed 1 part in
50,000 (i.e. an error of 1mm in the 50 metre tape) and the linear distance
between adjoining stations on the same traverse, should be within 1 part in
25,000.
1.12.3 Angular
error
The
angles of the traverse should be measured to a uniform degree of accuracy, and
the maximum misclosure at an azimuth station, or trigonometrical station should
not be greater than 12 Ö n seconds where "n" is the number
of traverse stations between azimuth control, thus, with 25 stations the
misclosure should be 12Ö25 = 60 seconds or less. The angular
adjustment per station should never exceed 5 seconds and seldom exceed 3
seconds.
1.12.4 Heights
carried through traverse
Heights
carried through the traverse by vertical angles should be correct to 1.5 metres
after closure adjustments have been made.
1.12.5 Terminal
control and azimuth control
Third
order traverses must start and finish at third or higher order control points;
and at intervals of 20 to 30 stations along the traverse; at permanently marked
stations an azimuth check should be made. The probable error of this azimuth
observation should not exceed 5².
Azimuth
observations should also be made at junction stations. At first sight, the
above standards may seem rather high, but, provided the chain is standardised
accurately, they should present no problem to experienced personnel. Angles
will usually be read with a Wild T2 theodolite, and the chaining will normally
be along the ground, not in catenary or suspension.
It
will be found that the initial linear surround is likely to be within 1 part in
12,000 to 15,000 or better.
1.13 Marking the Traverse
1.13.1 Permanently
marked stations
These
should be established at intervals of not more than 3kms along the traverse,
with an average distance of about 1.5 kms. Two reference marks, one of which
could be a reference tree, should be established at each station.
1.13.2 Marking
of intermediate stations
These
stations should be marked by temporary wooden pegs, about 25mm x 25mm x 200mm
1.14 Location
1.14.1 Access
Roads
and fences will usually greatly expedite the work, if one proceeds in the right
direction, and if the road does not carry heavy traffic or raise dust, to
hinder the work. The traverse should run just off the road edge, and about half
to one metre from the fence.
1.15 Traversing Party
1.15.1 Make
up of party
If
trained personnel are available and an efficient, economical party is required
in fairly open country, the four man party is suggested.
(a)
A theodolite
observer who reads and records angle and bearings in a field book.
(b)
A senior assistant
who holds the back end of the chain, and records field notes in respect to
chainage measurements, Abney Level slopes, and laid distances, references, etc.
Notes taken in this second field book will require transcription later on, into
the field book which records the angular work.
(c)
An assistant who
takes the front end of the chain, applies the required tension, and usually
reads the "reader", for any references required.
(d)
Another assistant
nominated as the "axeman", who clears the line, and sets the pickets.
If a vehicle can be taken near the line, and there is little cutting, the
axeman may be able to bring the vehicle along.
However,
there are many variations, even in the 4 man party. If the clearing is heavy,
the axeman and assistant may both cut, and the senior assistant may take the
front one of the chain, where he does the booking, leaving the theodolite
observer on the back end of the chain.
Or
the observer may do the booking of both angles and chainage, with the senior
assistant setting pickets, driving the vehicle forward, and taking the front
end of the chain. This will require a certain amount of walking by the senior
assistant.
Again,
in easy country, a 3 man party (axeman-picket setter; assistant; theodolite
observer) can make good progress.
A
5 man party, if available, may also be economically employed, (2 men clearing,
picket, setting and bringing on transport; one senior assistant; one assistant;
one theodolite observer.
A
party of 2 experienced, energetic men (observer and assistant) will also make good
progress where there is no cutting to be done.
All
the above work presupposes that the traverse stations are selected and located,
as the traverse proceeds, and that chaining is not done in catenary, but along
the ground. Reference marks on trees or corner posts should be observed and
measured as the work proceeds, but it must be decided whether it is economical
to emplace concrete blocks, and concrete reference marks, at selected stations
as the traverse is run, or at a later stage, this depends on the going, and the
availability of personnel.
1.16 Distance between Stations
1.16.1 This depends on the terrain,
and on the observing conditions. Along straight roads or fences, in gently
undulating country, 1.5 km legs are possible, in conditions of good observing.
In hilly, heavily timbered country, where a road is being traversed, it may be
difficult to see 100metres, on occasions, and special care in centring the
instrument becomes essential, to hold the azimuth.
On open plains, in hot weather, it may
be necessary to read the angles in the early morning, and late afternoon,
though the chaining can be carried out during the day. These, decisions must
be made by the party leader, depending on conditions prevailing at the time. Work
will usually be expedited by the use of the longest legs which can be observed;
if someone has to be sent to show up the forward or back pickets for the observer,
much time will be lost.
Assistants should be trained to keep
slightly off line, except when they are actually laying the chain, and so allow
the theodolite observer to read his directions, once the forward picket is plumbed.
With long straights, under open conditions, where the forward picket cannot be
seen with the unaided eye, it is the responsibility of the rear assistant, and
the observer to see that the chain is laid on line, or within 0.30m. Generally,
in flattish, open timbered, country, legs from 350 to 500 metres will give best
observing conditions and results.
1.17 Pickets or Targets
1.17.1 Pickets
Traversing
in bush country is likely to be carried out by observing to pickets cut from
saplings or branches, as work proceeds.
Such
pickets may be from 1 to 2 metres long, and 50mm to 75mm in diameter, sharpened
at the bottom for driving into the ground, and with a "step" cut in
the side 300mm to 450mm from the bottom, to assist such driving. The top 100mm
to 150mm, should he cut to a straight four-sided, tapering point, or to a
four-sided squared top with 25mm wide sides.
A
40mm x 50mm rectangular, or 40mm square, piece of white folded paper placed
carefully, and centrally on the pointed picket, leaving about 13mm to 25mm
showing, makes a good sight, however distance and visibility govern the size.
On
occasions, the point may not be seen and the paper will then need to be bisected;
it should therefore be carefully centred by the picket setter. If, for some
reason (such as stock in paddocks or along roads) the squared top picket is
adopted, a white papered top may assist visibility, and a strip of paper about
150mm x 50mm wrapped near the top makes a good sight for bisection. Spitting on
the last few millimetres, of the strip of paper, when wrapping it around the
pickets, is a crude but effective method of holding it.
A
pointed picket is an extremely dangerous object to be left standing in open
grazing country, on a road, or wherever animals could impale themselves. They
must not be left standing.
In
bushy country, it may be advisable to use pickets about as high as the
telescope of the theodolite. This will ensure that the observer will always see
his back picket after moving forward. Along roads, or in open country, the
observer will probably prefer to use pickets about 1 metre high, over which he
can set his instrument. The temporary wooden pegs, under each picket are often
more safely hit in by the observer, after he has set his instrument over the
picket. To counteract accidental bumps to the pickets before the instrument is
set up, the pickets should be accurately plumbed by the picket setter, and a
match (or hole made by the plumbob point) left to indicate the plumbed
position.
1.17.2 Targets
Special
traversing equipment is made by several firms. Instead of sighting to a picket,
a metal target in black and white is used, which may be screwed to the
theodolite tripod, and levelled with footscrews. For quickest results, the
theodolite tripod and target tripods are interchangeable. The tripods are set
up firmly, the targets levelled, and angles read with the theodolite the head
of which is then unscrewed and transferred to one of the tripods from which the
levelled target has been removed.
It
will be realised that with four sets of tripods, three targets and one theodolite,
a continuous series of steps can be undertaken with no hold-up. Work of the
highest quality is possible with such sets.
1.18 Field Chaining
1.18.1 Chains
Most
third order chaining has been done with the 300 foot steel band. However,
future chaining will be done with metric bands, probably the 50 metre band. The
characteristics of the 50 metre bands currently in use within the Division
are:-
Width 3mm
Thickness 0.05mm
Weight, approx. 0.680kg (1 metre = 0.013607kg.)
These
characteristics agree closely with those of the 300 foot band previously in use:
‑
Width 1/8²
(0.125")
Thickness 1/50" (0.02")
Weight approx. 2.51b. (1 ft =
0.0083 lb.)
It
should be mentioned at this stage that the 15lb tension applied to the 300 foot
band of approximately the same characteristics will probably be too great for
the much shorter 50 metre band, and would tend to pull the assistant "off
balance". A tension of 4.600kg (10.14lb) will probably be satisfactory for
the 50 metre band; however this could be the subject for further investigation.
1.18.2 Chaining
with the 50 metre band
Chaining
in catenary, i.e. with the tape fully suspended, or with one, two, or three
supports, is the recognised method of accurate chaining. The number of men
required, in a party engaged on such measuring, and the effect of wind, (nearly
always prevalent in the open areas of Australia) on the suspended steel band,
are the drawbacks to this method.
If
the ground chaining surface was perfectly flat, such as along a straight
bitumen road, along the rail of a railway line, or on a claypan, the tape could
be laid on the surface; with the correct tension applied, each end could then
be marked by a fine scratch or pencil line. However such conditions are
exceptional, and even under conditions with little or no undergrowth, it will
be found that rocks, grass tufts, etc., prevent the band from lying flat enough
to give an accurate horizontal distance. Also with the band completely along
the surface, accurate temperatures are much harder to obtain.
Thus
for normal field conditions with a small party it can be considered impractical
to either chain in full catenary or completely along the ground, therefore it
is necessary to adopt a compromise between the two methods.
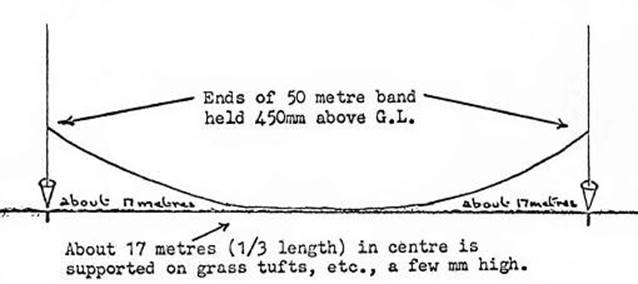
Figure 1.18.2(a)
Each
end of the band is held 450mm (approx. 18" or knee high) above the general
level of the ground, or of the vegetation which supports the tape. A
"pull" of 4.600 kg (approx 10 lb) is applied to one end of the band.
Under this tension the effect is for about one third of the band at each end to
be elevated with the central third supported a few millimetres above the ground
on low bushes, grass tufts, etc. This method of chaining counteracts slight
ground irregularities and obviates excessive low clearing. See figure 1.18.2(a).
When
using this method, a standard "sag" correction for each 50 metres is
determined at the time of standardization before the chaining task is
undertaken. See paragraph, "Check against standardized steel band."
If
high grass undergrowth supports the chain at a fairly regular height, the
senior assistant will estimate this general supporting height and have the band
held at the normal 450mm above this general height.
In
all cases temperatures should be taken at the general height of the band, not
with the thermometer lying on the ground, as this yields a highly inaccurate
temperature for a band held as described.
Use of plumbobs
The
skill needed to accurately use the above method is all in the use of the plumbobs,
and can only be acquired by plenty of practise. Sixteen ounce plumbobs of the
"conical" type, which enables easier viewing of the mark from directly
above, should be used in preference to the "pear shaped" type.
The
rear assistant has the most difficult task, he should double the surplus
plumbob string through the brass loop in the end of the band, holding this
string in the palm of the right hand, and using his right leg as a lever to
keep his right arm and hand steady, (the reverse for a left-handed person, in
all cases). The left hand should keep the plumbob string both at the right,
height and against the outer edge of the brass loop on the end of the band.
While waiting for the forward assistant to take up the tension, the plumbob's swing
should be continually "dampened" by tapping its point on the ground,
a few millimetres to the right of the mark. As the forward assistant takes up
the tension on the spring balance, the rear assistant allows this tension to
draw his plumbob directly over the mark; once there and steady, he calls loudly
"Mark" If this system is practised, and adopted, it will obviate the
"tug of war" so often seen with inexperienced assistants. See
Figures, 1.18.2(b) and 1.18.2(c).
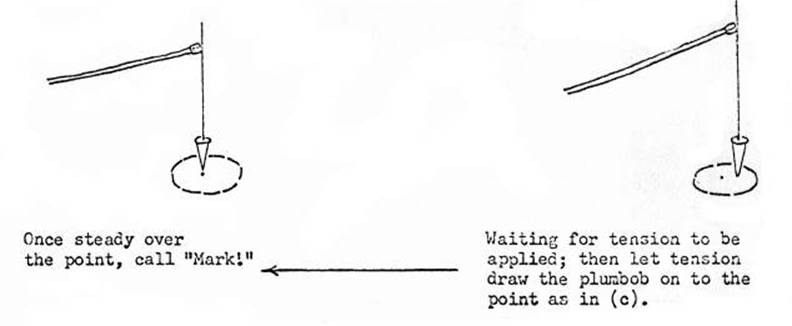
Figures, 1.18.2(c)
and 1.18.2(b)
Check against standardized band
One
50 metre band should be properly standardized and held solely for the purpose
of standardizing field bands. Ideally, this band should be of
"invar"; also all steel bands should have the same characteristics. A
suitable tension for field use should be adopted for standardization; this
saves the calculation of a correction for tension and the need to apply it to
every length laid in the field.
The
field bands should be checked against the standard band in two ways, i.e.:‑
(a)
On a perfectly
flat surface, in the shade, lay out an exact 50 metres with the standardised
band. Use the correct tension and apply a temperature correction, if necessary.
Each
field band is checked against this base at the same tension, and the temperature
recorded. The difference in measurement gives the error of that particular 50
metre band at that temperature. This difference would only be used to
correct any 50 metre length which may be chained along the ground.
(b)
Using the exact
method to be employed in the field task, a full 50 metre length is laid out against the exact 50
metre base, the temperature is taken and the difference in measurement is
noted. This difference will be a set correction covering "sag",
"tension", and "error in length" for each 50 metre length
laid at a corresponding temperature. Thus only temperature corrections need to
be calculated for each length laid in the field. It is unlikely that many lengths
will be laid completely along the ground, however it is a simple matter to make
the check outlined in (a) above in case some lengths are more conveniently laid
on the ground.
The usual procedure in laying the chain
is briefly:-
(a)
The forward assistant
pulls the chain ahead, taking care that it does not go under bushes or rock snags,
and counting his paces, to stop approximately at the correct distance. He will
have to get used to the pace-metre ratio.
(b)
The chain is
straightened by "throwing up" each end, holding it lightly taut, and
throwing a wave motion along the tape. Two hands should be used, one hand holding
the end by balance or plumbob cord, the other stretched as far along the tape
as possible to help in "throwing up" the tape, in the small wave
motion mentioned. Do not jerk the chain sharply.
(c)
With chain
straight and free, the front assistant puts on the 4.600 kgs (about 10lbs)
tension to obtain an approximate position for placing the arrow. He eases off
the tension, and with his heel kicks away the grass, etc., to make a clear spot
for the plumbob mark.
(d)
He again applies
the 4.600 kgs tension, holds his plumbob string right at the end of the chain,
and lowers the plumbob to about 25 to 50 mm above the ground. The rear
assistant holds his plumbob string at the rear end of the chain, with the plumbob
point 12mm or less, above where the arrow enters the ground. Both assistants
are holding the chain ends 450mm above the general supporting height of the
tape.
(e)
When the tape is
steady, it is kept thus for 3 or 4 seconds, and the front assistant drops his
plumbob to make a light mark on the cleared surface. Then he eases off the
tension. If either assistant is dissatisfied with the laying of the chain it
must be done again.
The
front assistant carefully inserts an arrow, slanting and at right angles to the
line being traversed, in the centre of the plumbob mark. This completes the
laying of one length of the chain, the procedure being repeated as many times
as necessary. The above method of chaining gives a distance, for each length of
chain laid, that is slightly short of the length of the chain; each 50 metre length
will need to be corrected by the standard correction covering "sag",
"tension", and "error in length" that was ascertained in
the check against the standardised steel band. In addition each length laid
will be subject to the temperature correction for the prevailing temperature.
1.19 Field Chaining – Odd Lengths
At
the end of a traverse leg there is usually some odd length to be measured. The
method is for the front assistant to hold his end of the chain at the peg, whereupon
the rear assistant pulls the chain back until he, the rear assistant, is
holding on a brass mark. The front assistant then reads the odd length, on the
reader, at his end of the chain when tension is applied. On arrival at the peg,
the rear assistant should be shown, and should check this intercept, and should
report the value of the brass mark that he plumbed. (See Figure 1.10.2) Roller-grips
for odd lengths are very desirable, and should always be used, if available. In
all chaining, the body should be used to take the tension by resting the elbow
just above the bent knees, or if the chain support is higher, by pressing the
elbows or wrists hard against the body.
1.20 Corrections to chained distances
The
following are brief notes on the corrections which affect third order
traversing.
1.20.1 Standardisation
Normally,
one tape has been standardised by an authority such as a State
Lands Department for a small fee. A sample certificate can be seen here. Before commencing a task, field tapes have been checked against this tape as explained in 1.18.2.
1.20.2 Slope
correction, and use of the Abney Level
This
is the most frequent, and usually the largest correction applied in chaining;
its purpose being to reduce measurements which have been taken on sloping
ground, to horizontal measurements.
These
slopes, or angles of elevation or depression, are generally read with an Abney
Level; the rear assistant reading the same height (eye height) on the forward
assistant. There is a probable error of 5 minutes with such a reading. This is
not a cumulative error, but has a serious effect on corrections for slope over
4°. For these the theodolite should always be used.
In
hilly country, where large slopes are common, consideration must also be given
to chaining in catenary, so that accurate slopes may be determined.
Slope
corrections are calculated by multiplying the versine of the slope angle, by
the measured length. These corrections are always minus, whether slopes are
elevation or depression.
A
table of slope corrections for every 5¢ from 0° 25' to 5°, and covering
the distances in use, is the quickest way to reduce slope distances, in normal
country.
Natural
versine values for every minute are listed in Chambers Mathematical Tables, and
some slide-rules incorporate a versine scale.
1.20.3 Temperature
correction
Since
steel expands when heated, a chain standardized at 15°C (59°F) and used in the
field at 32°(approx. 90°F) will be too long; requiring a plus correction, for
temperature, for all measurements made with it.
A
coefficient of expansion for steel chains may be taken 0.000 0113 per 1°C
(0.000.0063 per 1°F). A table showing the correction for temperature and length can be seen here.
The formula for temperature correction
is:-
Ct = 0.000 0113 L (T-To)
where Ct =
Temperature correction.
0.000 0113 = co-efficient of
expansion of steel per 1 C.
L = Measured length.
To = Temperature of
standardization of to
T = Temperature of
tape in field, in °C
It
is difficult to obtain accurate temperatures in the field; temperatures can be
as much as 1° to 5°C in error, usually too high. If conditions are normal, it
is not necessary to read a temperature at every length laid, and a reading
every fourth tape laying should suffice.
Care
should be taken to see that such temperatures are read at the height of the
chain; that is, when chaining across foliage which supports the chain, at about
300 mm above the ground, the chaining thermometer should be laid horizontally,
and at that height; not laid on the ground, which on a hot day with a light
breeze, might give an error, of 5°C, or more, too high.
If
the thermometer is placed at the correct height, then the chain laid, and the
slope read and booked, enough time should have elapsed for the thermometer to
have moved to the correct temperature.
Inver
bands are sometimes used. This is an alloy of nickel and steel, with a very low
coefficient of expansion, approximately 1/30th that of steel. If
standardisation is made close to the prevailing field temperatures, then
temperature corrections may be disregarded with these bands.
1.20.4 Tension
correction
This
is a correction which should seldom be necessary. If the tape is standardised
at a correction suitable for field use, and used at the same tension, no
correction is necessary. The formula for computing variation in tension is:-
Cp = { (P – Po) L} / AE
where Cp
= The correction per distance L, in metres.
P = Applied tension in Kilograms.
Po = Tension of tape at standardisation,
in Kilograms
A = Cross-sectional area, in square
cm's.
E = Young’s Modulus of elasticity
of the steel in the tape
taken at 2,003,750 Kilograms per
square cm.
1.20.5 Sag
correction formula
Where W = Weight of tape
in kilograms per metre.
L = Length of unsupported tape,
in metres.
P = Tension in kilograms.
Sag correction Cs = { W2 *
L3 } / {24 * P2 }
When a tape is supported in
equidistant spans, this formula becomes:-
Sag correction Cs = n [ { W2
* L3 } / {24 * P2 } ]
where
n = Number of equal spans into which tape is divided.
L = Length of each span in
metres.
With
slopes over 10°, a further factor is introduced due
to the deformation of the catenary.
Formula
for Sag correction on slope = sag correction on level x Cos2 slope
angle.
To calculate sag using SI units this article is useful.
This
will rarely be necessary. Since sag reduces the length, the measured distance
is longer than the actual distance, so correction “negative”.
1.20.6 Sea
level Correction
This
will rarely be applied in the field. Generally mean height can be used for the
traverse, the sea level factor is set on a computing machine, and all measured
distances are multiplied, in turn, to give a sea level distance.
1.21 Summary of chaining Corrections and Errors
1.21.1 Standardisation
If
incorrectly standardised, the one tape will give an accumulating error of the
one sign. Tapes should be carefully standardised, under good conditions.
1.21.2 Errors
in slope reading
Where
slopes are read with the theodolite, errors should be negligible. When the
Abney Level is used, and is checked every few days, against the theodolite,
errors of reading should cancel out, in lightly undulating country.
1.21.3 Temperature
The
main source of error likely to occur, is from placing the thermometer at a
different height from the tape; usually too near the ground which will make the
readings too high.
A
general mean of conditions, to which the tape is subjected, should also be
chosen for the thermometer; that it is not protected from the wind, or put in
the shade, unless the tape is under such conditions. The thermometer should be carried
vertically so that the mercury column is not shaken apart, but laid horizontally,
at the mean height of the tape, and given a chance to settle before reading. Much
time can be lost, and little extra accuracy gained, through elaborate
temperature reading, but reasonable care must be taken. Temperature errors are likely
to be cumulative, on the one day, under similar weather conditions, and usually
too high.
1.21.4 Tension
If
the spring balance is reading incorrectly, this will give a cumulative error.
It is advisable to check all balances, by lifting a known weight, or by pulling
against the other balances.
1.21.5 Sag
In
uneven country, sag must be watched carefully, and it will be decided whether
to chain in catenary. Sag errors will rarely occur in easy, flattish, terrain.
They are cumulative.
1.21.6 Alignment
Keep
alignment within 150 to 300mm, and no appreciable error will result. Alignment
is more easily maintained by the rear assistant, who should direct the front
assistant on line before laying the chain.
1.22 Algebraic signs of errors using a single tape
When speaking of chaining errors:-
“+”
means an error which tends to make a distance measured longer than it actually
is, on the ground; thus the correction to the measured distance is MINUS.
“-“
means an error which tends to make a distance measured longer than it actually
is, on the ground; thus the correction to the measured distance is PLUS.
The following list of errors shows the
accumulating effect.
|
|
Error
|
Accumulating
effect
|
|
a
|
Standardization
|
All plus or
all minus
|
|
b
|
Slope
|
Plus &
minus
|
|
c
|
Temperature
|
Plus
usually
|
|
d
|
Tension
|
All plus or
all minus
|
|
e
|
Sag
|
All plus
|
|
f
|
Alignment
|
All plus
|
|
g
|
Height of
tape
|
Plus &
minus
|
1.23 Errors of a full chain
Every
distance laid must be entered, at once, in the field notes. Recourse should never be made to the
counting of arrows, or to both assistants trying to remember the number of full
lengths laid. The dropping of one full length is the most frequent source of
gross error in chaining. Occasional wooden tally pegs, (about every ¾ kilometre)
are useful, in case an arrow should be accidently knocked out, on a long
traverse leg. This can prevent returning to the beginning of the leg.
1.24 Check measurements
These
should be made if possible; more especially on large surrounds, to pick up
gross errors. They may be made later, or by a second pair of assistants
following the traverse party, and a lower order of accuracy is possible. Slopes
and tensions are read, but not temperatures and other refinements.
1.25 Angular measurements
Angular
measurements will normally be made with the Wild T2 theodolite, or similar
instrument.
1.25.1 Horizontal
Angles
The
mean of 2 rounds is adopted as the observed angle at each station; each round
consists of a face left and a face right pointing, on the distant stations.
Settings are approximately:-
FL 000° 00’ 30" returning to
the RO on 180° 00’ 30" approximately.
FR 270° 05’ 30" returning to
the RO on 090° 05’ 30" approximately.
The
RO should always be the backsight, and the difference between the pointings
should not exceed 10 Seconds.
1.25.2 Vertical
angles
Heights
are carried through the traverse by vertical angles. Two pointings, a face right,
and a face left, are read from each station, to both backsight and foresight,
and always that order. The heights of the instrument, and of both targets are
recorded in the field book, as each is measured.
1.26 The Surveyors Level
The
function of the surveyors level, more commonly termed simply, the level, is to
establish a horizontal line of sight, or nearly so. In its simplest form, it
consists of a telescope with a defined line of sight and a spirit level tube to
enable this line of sight to be set in a horizontal plane.
The modern levels which are likely to
be met with, are:‑
The
Tilting Level, and
The Automatic Level.
An
almost obsolescent level is the Dumpy Level which had the telescope body fixed
at 90° to the vertical spindle.
1.26.1 The
Tilting Level
The
main features of the telescopes incorporated in Surveyors Levels are that they
have low magnification and a small field of view, suitable for accurate sighting
over the short distances required. The diaphragm normally has a central
horizontal and vertical wire; in addition two horizontal "stadia"
wires are set equidistant, above and below the central horizontal wire. They
are normally set so that the distance read on the staff between these two wires
(known as the "intercept" or "S") is one hundredth of the
distance between the level and the staff when the line of sight is horizontal.
Ratios, other than one to one hundred can be ordered from the maker, if
required.
The
spirit level attached to the telescope is similar to those used on theodolites,
and provision is also made for its adjustment in a similar manner.
To
operate the instrument, the telescope with its attached level tube can be
levelled by a finely pitched screw - called the tilting screw - independently
of the vertical axis, and in consequence the line of collimation is not in
general at right angles to the vertical axis. In using these instruments, the
axis is set only approximately vertical with the three footscrews with
reference to a circular bubble. Before reading the staff, the bubble in the
main level tube which is attached to the, telescope, is centred exactly by
means of the tilting screw.
In
better instruments this is done by bringing the ends of a split bubble into coincidence.
The bubble ends and the staff are viewed through the telescope at the same
time, and coincidence of the bubble ends is made at the instant of reading the
staff. Mirrors to read the bubble are used instead of the split bubble on low
priced instruments.
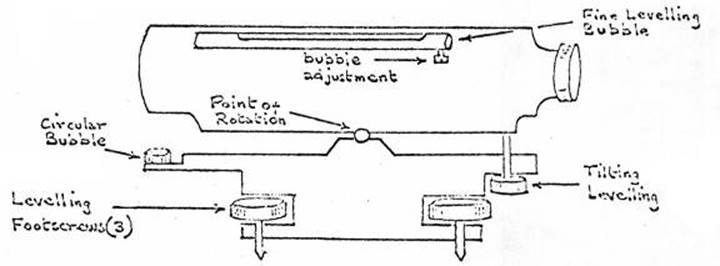
Figure 1.26.1(a)

Figure 1.26.1(b)
1.26.2 The
Automatic Level
All
leading surveying instrument manufacturers now have automatic levels available
and at least one theodolite incorporates the system, instead of the alidade
bubble, for use when observing vertical angles.
In
appearance the automatic level is just like any conventional level; it has the
usual three footscrews for levelling with the small circular bubble. However
the orthodox bubble attached to the telescope has been abandoned. In its place
are three prisms; one system has two of these prisms rigidly connected to the
telescope tube with the third hung to swing freely; another system has one rigid
prism with two swinging freely. A damper is incorporated to steady the line of
sight and the whole unit of prisms and damper is called the "optical
stabiliser".
The
basic concept of the automatic level is that swinging freely, under the
influence of gravity, the stabiliser automatically aligns the line of
sight on the wires and in the horizontal plane, i.e., ninety degrees to the
plumb line even though the telescope itself is slightly tilted. The range of
the stabiliser of a good automatic level is plus or minus twenty minutes (±20¢)
and this is well taken care of if the instrument is levelled with the small
circular bubble, which however must be kept in adjustment.
It
should be noted that most modern automatic levels give an upright image. The automatic
level should be carried with the telescope in a vertical position, so
that the stabiliser is at rest, when ravelling from job to job. The type of
carrying case supplied by the maker usually takes care of this.
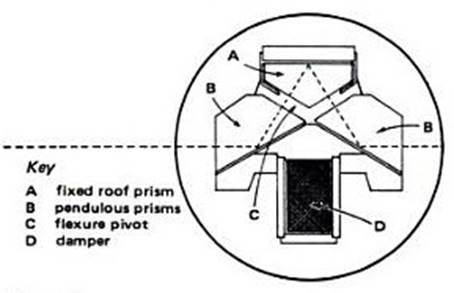
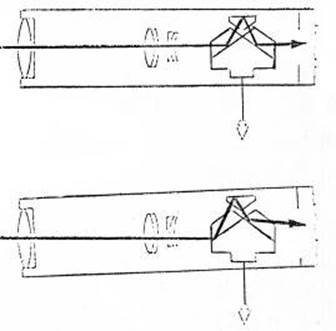
Figure 1.26.2. The
Watts “Autoset” stabiliser and principle of operation.
In the “Autoset”
level telescope there is the stabiliser consisting of two prisms on a suspended
mount.
If the “Autoset” is
tilted the stabiliser swings like a pendulum and keeps the horizontal ray on
the cross-lines automatically
1.26.3 Level
Tripod
The
tripod is similar to that used for theodolites, the main difference being the absence
of a moveable centring device. The same care should be given to the level tripods
as is given to the theodolite tripod or the quality of the observations will
suffer; check for loose bolts, screws or ferrules and keep the tripod well
varnished.
1.26.4 Staff
Many
types of staves are available, however the one most likely to be encountered at
present is the "Sopwith" two piece hinged type, or the "Sopwith"
three piece telescopic type, both of which are graduated in feet and
hundredths.
Figure
1.26.4(b) shows this system of graduating the staff and indicates the method of
reading these graduations.
The
telescopic staff is easier to carry, however the more rigid two piece hinged
type is more accurate since it maintains its length better over a period of
time. It also usually has a, circular staff bubble attached, while the telescopic
type requires a hand held staff bubble. Needless to say, all staff bubbles must
be kept in adjustment.
Foot-metric
staves are also available. With these, all readings are taken both in feet and
metres, thus providing constant checks and greater accuracy.
All
staves should be carefully looked after, kept clean and dry and always returned
to their carrying cases when not in use. When carried in the vehicles they
should preferably be strapped high up inside the vehicle to prevent damage from
digging tools or other heavy sharp equipment, as will occur if the staff is
laid on the floor.
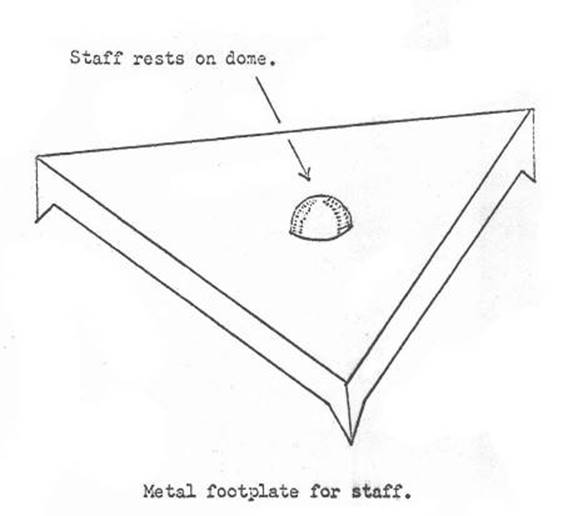
Figure 1.26.4(a)
A steel
footplate, upon which to stand the staff at change points, is necessary to
ensure a firm base at such points. A suitable type is shown in Figure 1.26.4(a).
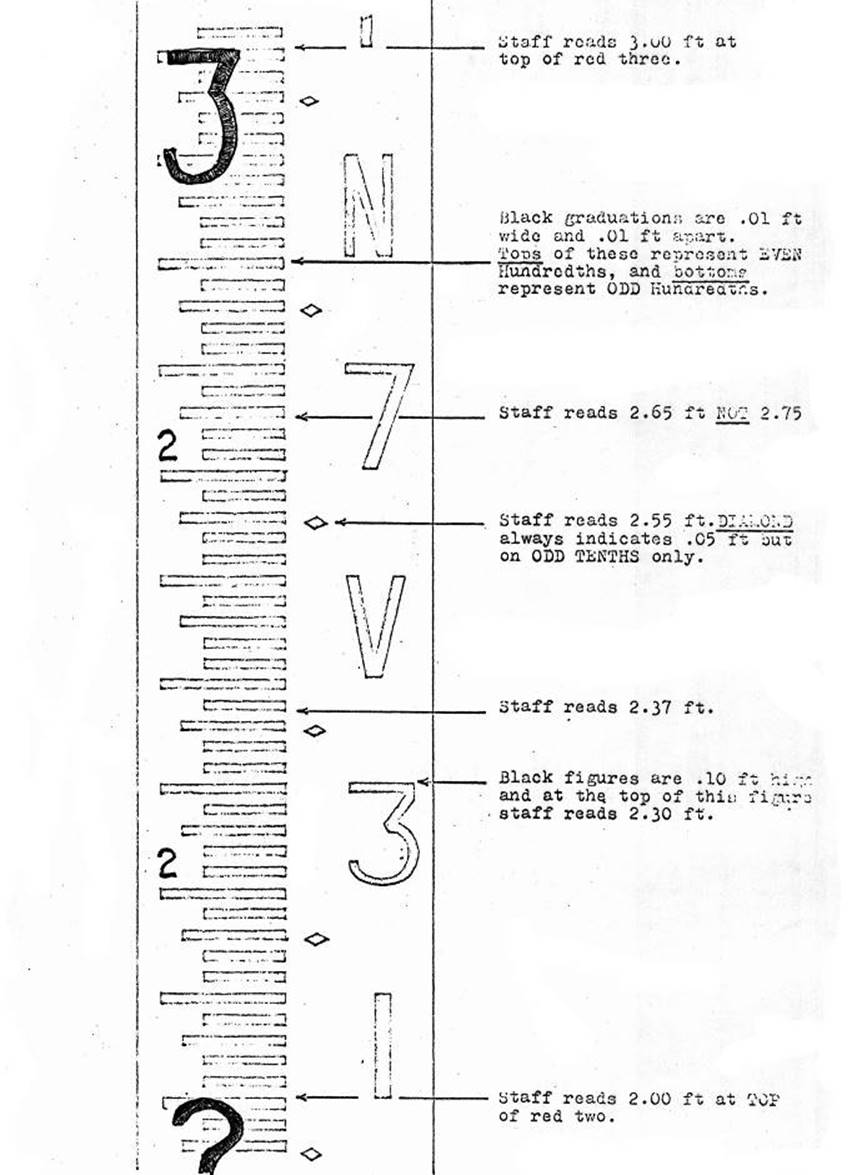
Figure 1.26.4(b)
Levelling Staff “Sopwith” type.
1.26.5 Testing
and adjusting the Surveyors Level
The
"Two Peg Test" is used to ascertain any error in either a Tilting or
an Automatic level. The test will be described first and the adjustment to each
typo of level will be described in general terms. However it is advisable to
consult the handbook of the particular brand of instrument in use before
adjusting any instrument with which the user is not familiar.
Two Peg Test
(i)
Two points A and B
are selected 200 feet apart and pegs driven in firmly.
(ii) The level is set up at C, midway
between the marks (plus or minus a couple of feet). Carefully take readings to
a staff held on A and B in turn. The difference between those is the accurate
difference in height regardless of the adjustment of the instrument. This is
because the horizontal distances AC and BC are the same; therefore if the line
of sight is not horizontal, both staff readings will be an equivalent amount
too high or too low. See Figure 1.26.5 (a).
(iii) Move the level to the vicinity of Peg A;
set up on an extension of the line AB at minimum focus distance from the peg
(about 6 feet). Again carefully take readings on the staff, hold on A and B in
turn. If the difference between these two staff readings does not agree with
the, difference in height as found when the staff readings were taken from the
mid-point, the level needs adjusting. See Figure 1.26.5(b).
Unless
the instrument has a large error, it can be considered that the line of sight
and the horizontal line as shown at rA in Figure 1.26.5(b) are so close that no
different reading on the staff at that point could be made after the bubble was
adjusted.
Therefore
the reading A of 4.68 - the accurate difference in height of 1.93 would give
the point where the horizontal line would cut the staff at B, i.e. 2.75. See
Figure 1.26.5(c).
Procedure where the instrumental error
is large
If
the error is known or thought to be very large, instead of making the second
set-up of the instrument at minimum focus from the staff, it should be set up at
a known distance on the extension of the line AB. This known distance should be
some convenient fraction of the distance AB, for example AB = 200 ft, setup at
20 ft from A, ratio 1:10. Proceed with the test, noting that by similar
triangles, a correction to the line of sight will need to be made at both peg A
and peg B and that it will be in the ratio 1:10. See figure 1.26.5(d).
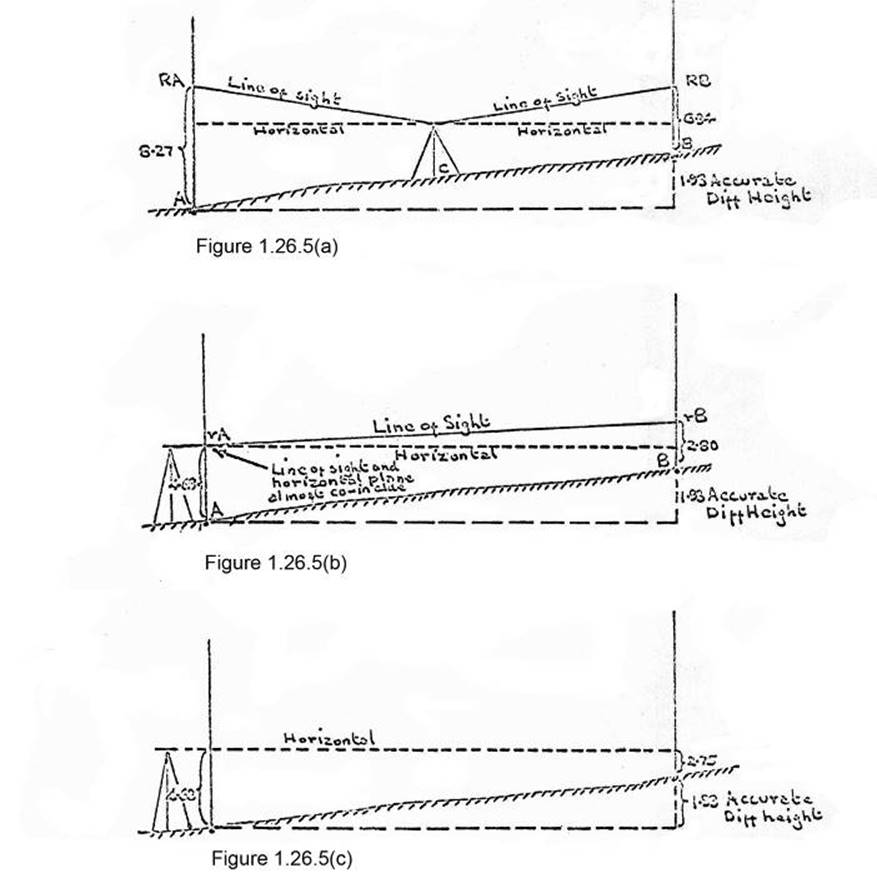
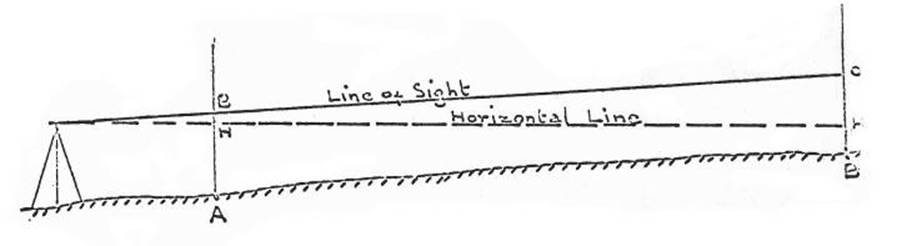
Figure 1.26.5(d). Triangles
IHB and IHC are similar;
therefore the error
in the line of sight at BH is 1/5 the error at CH.
Adjusting the tilting level after the
Two Peg Test
The
staff is taken to peg B, and the central crosswire is laid on the staff with
the tilting screw at the calculated correct reading, in the case of the example
from Figures 1.26.5 (a,b & c) it is 2.75. Naturally this moves the ends of
the split bubble apart but the line of sight is now horizontal.
With
the bubble adjusting screw, the ends are then brought into coincidence
thus the line of sight remains horizontal and the bubble is now in agreement
with the horizontal line as defined by the line of sight through the central
crosswire of the telescope.
To
check the instrument, take a couple of careful readings on the staff which is
still at A, bringing the bubble ends into co-incidence with the tilting screw
in the normal manner, move the staff to B and repeat. The difference in the
readings rA - rB should now agree with the difference height.
Third
order levelling specifications state that the vertical collimation error must
not exceed ten seconds of arc, which is just on 0.01ft at 200 feet, therefore
if agreement is within 0.01ft no further adjustment is necessary. If the
difference is greater than 0.01ft repeat the adjustment until this accuracy is
achieved.
Adjusting the Automatic Level after the
Two Peg Test
The
staff is taken to peg B, and the central crosswire is brought onto the staff at
the calculated correct reading, in this case 2.75, by means of graticule
adjusting screws.
Thus the central crosswire has now
been brought into coincidence with the horizontal line of sight as defined by
the stabiliser unit and this line will be correct unless the stabiliser has
been damaged. To check that the adjustment has been performed correctly proceed
exactly as for the check of the adjustment to the tilting level.
1.27 Level Traversing – Hints
1.27.1 The
Instrument and type of levelling
The
instrument to be used would most likely be the Watts "Autoset", or a
similar type of automatic level.
The
tasks likely to be encountered will most likely be level traverses with few, if
any, intermediate points. In mapping surveys "grids" of levels are
rarely required.
1.27.2
Extracts from
"Specifications for contract Third Order Levelling
(i)
Vertical
collimation error of instruments shall not exceed ten seconds of arc (0.01ft at
200 feet). Field tests to be made before work commences each day. Tests to be
booked on 1 complete page of the fieldbook immediately preceding that day's
level observations. Results are to indicate the error before, and residual
error after adjustment, together with distances over which the test were
conducted.
(ii) Periodic tests to be made to ensure
proper adjustment of the staff bubbles.
(iii) With Automatic Levels:
(a)
The circular
bubble must be in precise adjustment at all times.
(b)
Each time the level
is set up to take readings, the dislevelment shall not exceed the tolerance
laid down in the manufacturers hand book.
(c)
To mitigate
systematic error due to dislevelment of the horizontal plane, the following
routine is to be followed:-
At
consecutive bays, level the instrument with the telescope pointing in opposite
directions, i.e. at first and third setups the telescope should point towards
the backsight, and at second and fourth setups the telescope should point
towards the foresight.
When
two staves are employed and the staffmen are "leap frogging" this is
resolved by always pointing the telescope at the same staff when levelling the
instrument.
(d)
To ensure the
stabiliser is free to oscillate, prior to every reading the telescope is to be
turned slightly in one direction then the other.
(iv) Placement of the Staff
(a)
Bases to be
inspected and cleaned if necessary at every change point. The staff shall
always be placed on a steel footplate at each change point, unless change point
is a Bench or other station mark, temporary BM, concrete culvert, firmly driven
survey peg, etc.
(b)
When two staves
are being used, there must always an even number of instrument stations between
consecutive BM's so that the same staff is placed on the starting mark as a
backsight and on the next as a foresight. This eliminates any zero error i.e.
the graduations of the two staves.
(v)
Length of sights
(a)
The length of any
sight shall be such as to allow the positive resolution of the staff graduations,
and no sight shall exceed three hundred feet, even under conditions of very
good visibility. (As a general rule, it is advisable to keep sights to about
200 ft. Also see that the centre of the graticule is kept higher than one foot
from the base of the staff to prevent refraction causing errors in rays which
are too close to ground level).
(b)
As shown in the
notes for adjusting the level, back and fore sights should be balanced at the
same length to help mitigate any instrumental errors: this is probably best
controlled by dragging a standard long rope; when only a short sight can be
obtained because of a steep slope, the next sight must be a correspondingly
short sight, even though a normal length sight could have been made. Upper and
lower stadia readings are always recorded to prove that the sights have been
balanced and to measure the overall length of the traverse.
(vi) Accuracy
In
general, the forward and back levelings of a section (or, in the case of a
loop, the closure on the commencing station) shall not differ by more than ± 0.05
ÖM
feet, where M is the distance in miles between the BM's (or the length of the
traverse in the case of a loop).
For
details of checks for accuracy of all cases that may be met with in
third order levelling consult the appropriate specifications, section 5.1.
1.27.3 The
Level Field Book : Rise & Fall Method
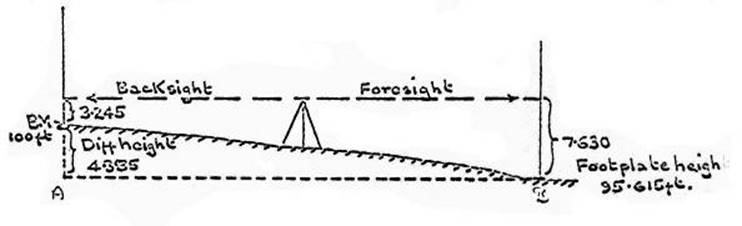
Figure 1.27.3(a)
Figure 1.27.3 shows the procedure when
levelling:-
Step
1: The staff is set up on the BM, termed point A in the diagram, height 100 ft.
Step 2: The level is set up about 200
feet from A along the line of advance.
Step
3: The second staff is setup on the steel footplate at change point B, a
further 200 feet along the line of advance.
Step
4: A reading is taken on the staff held at A; this is booked as a backsight,
and in this example is 3.245 ft. Note that sights of 200 feet or under should
be read to the nearest 0.005 ft. Stadia readings to the nearest 0.01ft are also
taken.
Step
5: A reading is taken on the staff held at B, this is booked as a foresight,
and in this example is, 7.630. If only one staff is available the observer must
wait for the staffman to move from A to B before this reading can be taken.
Step
6: As the foresight is larger than the backsight B is lower than A, therefore
the difference between the backsight and the foresight is booked as a “fall” in
the appropriate column, i.e. 7.630 - 3.245 = a "fall" of 4.385,
therefore the height of B is 100 - 4.385 = 95.615 feet.
A
suitable field book layout is shown in Figure 1.27.3(b). This is eminently
suitable for a level traverse, without intermediate sights and using either a
foot or metric staff. In the case where the foot/metric type staff is to be
used, the extra columns for metric readings are provided on the right hand side
of the field book page. The appropriate lines are "blanked out" to
ensure that the first foresight is written one line below the first backsight.
Checking the Reductions
Backsights
and Foresights are totalled at the foot of each page, as are the Rise and Fall
columns. The difference between the Backsights and Foresights is noted and this
should be the same as the difference between the Rise and Fall columns. It
should be noted that to apply this method of checking, the first sight on the
page of levels must be a backsight and the last sight on the page must be a Foresight,
with this entry repeated as a Backsight as the first entry of the next page.
Where
a Reduced Level value is available for the commencing BM, Reduced Levels are
carried forward in the appropriate column, this gives a further check on the
reductions as the difference between the first and last Reduced Levels should
be the same as that of the difference between the total Backsights and total
Foresights, and the difference between the total Rise and the total Fall.
This
book is hardly suitable for use when booking a "grid" of levels with
many intermediate sights. In that case it probably would be better to
especially rule up a plain fieldbook to suit the task in hand. Where only a few
intermediate sights are required the fieldbook described could be used by
entering these sights in one of the columns designed for metric readings,
providing of course that the foot/metric staff is not being used.
1.27.4 The
Level Field Book : Collimation Method
This
method which is suitable for certain types of engineering surveys - the booking
for a stadia traverse with a theodolite is a variant of the Collimation Method
- is unlikely to be met with in mapping surveys; however the following
explanation and example is provided.
The
method consists of finding the Reduced Level of the line of sight at each
station (referred to as the Reduced Level of height of Instrument, or just
height of Instrument) and subtracting from this value the reading on the staff
at each point to obtain the reduced level at that point:-
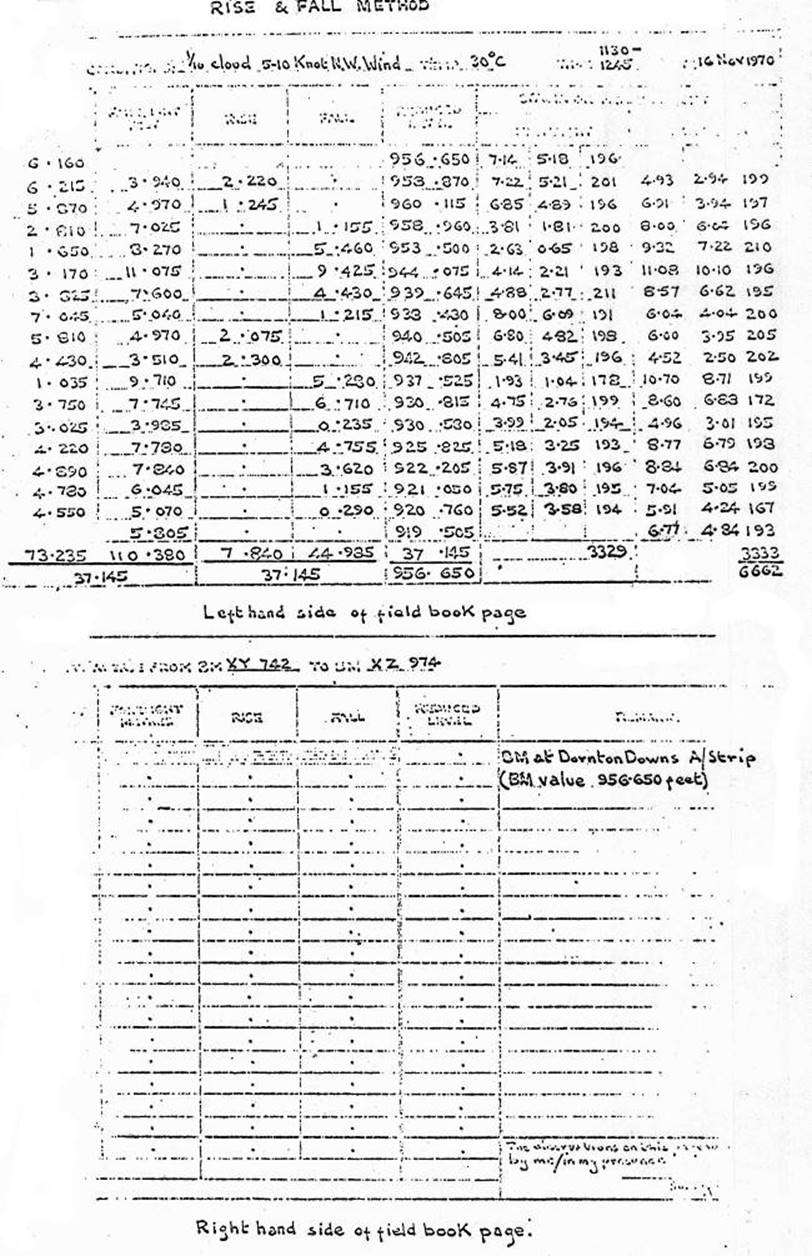
Figure 1.27.3(b)
Step1. This R.L. Line of sight is
always found by adding the backsight reading to the R.L. of that station.
Step
2: From this Line of sight, the RL, of the forward station is always found by
subtracting the foresight reading on the staff. See Figure 1.27.4(a).
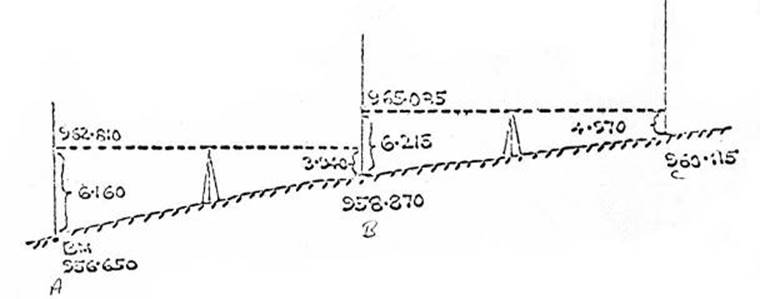
Figure 1.27.4(a)
In
the above Figure, RL of A = 956.650 + backsight reading on staff 6.160 =
962.810 which is RL, Line of sight (or height of instrument). Then 962.810 - reading
on staff at B, 3.940 = RL of B is 958.870, and so on.
One
check only is available, i.e. that on any page the difference between the total
backsights and the total foresight should equal the difference between the R.L.
of the commencing and final stations on that page, providing of course that the
first entry on the page is a backsight and the closing entry a foresight.
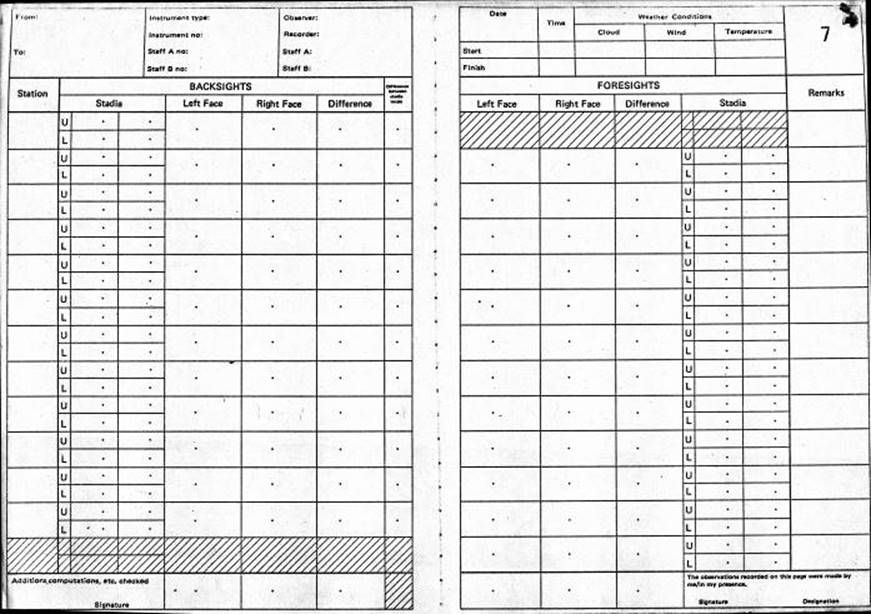
Levelling Field Book
page.
2 Theodolite – General Description
2.1.0 General Description
The theodolite is an instrument for measuring horizontal and vertical
angles. There are numerous types, but they all have the following essentials.
2.1.1 A
"lower plate" revolving about a hollow vertical axis, and fitted with
a graduated circle. It is also provided with a circle setting screw, so that
the circle can be set at any selected point in its rotation.
2.1.2 An
"upper plate" which rotates about a vertical axis, fitted into, and
concentric with, the axis of the lower plate. To this upper plate are rigidly
attached a pair of standards and a levelling bubble. It also carries the
horizontal clamp and tangent screw, and the reading device, normally a
micrometer.
2.1.3 An
"Alidade" which is the name given to the combination which consists
of the horizontal axis, telescope and vertical circle together with a levelling
bubble. The vertical circle is fitted with a clamp and tangent screw, for use
in measuring vertical angles. The "alidade" bubble is fitted with an
adjusting screw, either of the ordinary tangent type, or fitted with a
lock-nut, to set the zero in its correct position.
2.1.4 Other
parts are, levelling screws by which the axes of the plates can be set truly
vertical, a traversing head with which the instrument can be moved for a short
distance, in any direction, without disturbing the tripod; and a plumbob
suspended from the centre of the vertical axes, with which the instrument can
be set up, vertically, above a point on the ground.
2.1.5 For
a theodolite to be in perfect adjustment, the following requirements must be
fulfilled:-
(a) The horizontal axis must be truly perpendicular to the vertical
axis.
(b) The line of sight, as defined by the cross hairs in the telescope,
must be truly perpendicular to the horizontal axis.
(c)
The centre of rotation, of the
upper plate, must coincide, with great precision, with the centre of the
graduations of the circle, on the lower plate.
(d) At least one levelling bubble must have its axis truly
perpendicular to the vertical axis.
(e) The alidade must be so adjusted that, when the vertical axis is
vertical, the reading on the vertical circle correctly indicates the
inclination of the line of sight.
2.1.6 When
these conditions are fulfilled, if the instrument is "Levelled"
(i.e., if the, levelling screws are adjusted until the bubble remains central,
for a complete revolution, about the vertical axis) it will be possible
correctly to read horizontal and vertical angles.
Figure
2.1.7.
2.1.7 It
must be realized that when the instrument is in adjustment, the line of sight
traces out a vertical plane, at right angles, to the horizontal axis, as the
telescope is elevated, or depressed.
If the theodolite is set up at "T" (Figure 2.1.7.) and
the telescope directed, in turn, first to "A" and then to
"B", the angle read is the angle between the vertical planes passing
through TA and TB. That is to say, if perpendiculars are dropped from A and B
to the horizontal plane containing T, the angle read is that subtended by the
feet of these perpendiculars, and not by the points A and B, themselves, unless
those points happen to be on that horizontal plane.
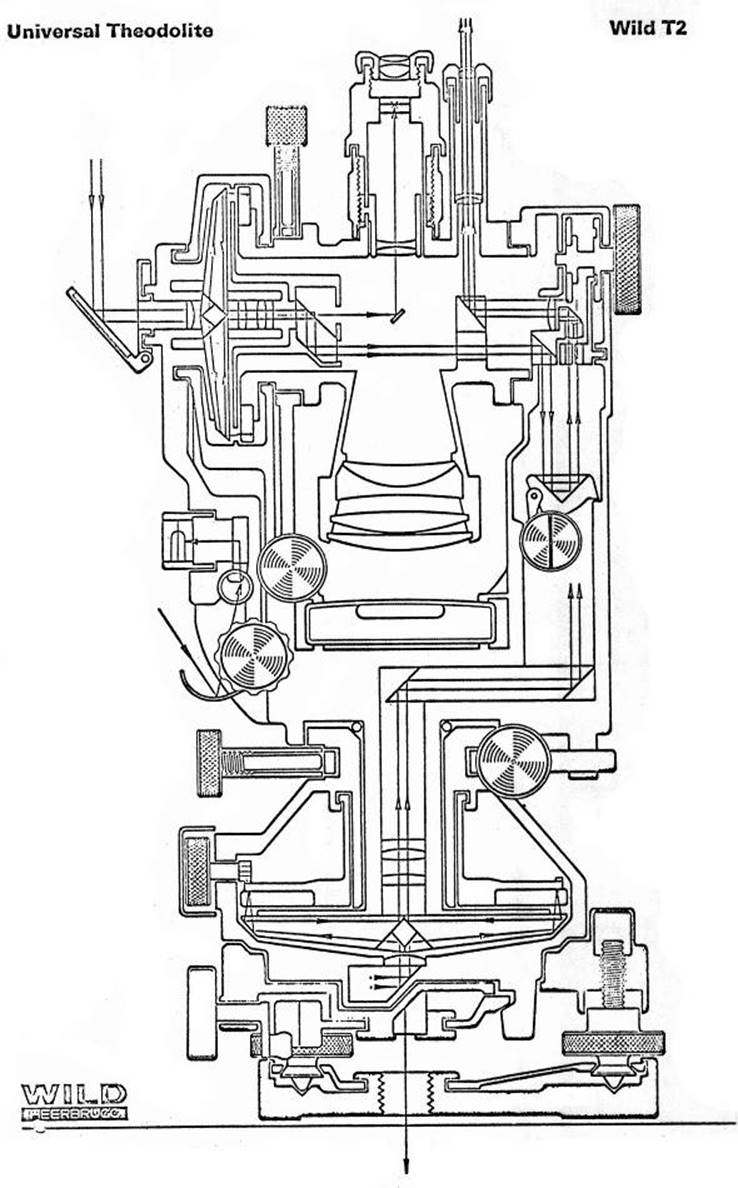
3 Theodolite – WILD T2 - its use in all types of
observation
3.1.
General preparation.
While
not the official Wild T2 manual this version provides very similar
information.
3.1.1 Care
and adjustment of the instrument and tripod
At the end of each field season, the theodolite will normally be
completely overhauled by the maker, or agent, and should be issued in tip top
condition for the season’s work. Only minor adjustments are to be made by the
party leader or observer, in the field.
Before leaving for the field the instrument should be checked to
see that no fault has been overlooked in the laboratory by the maker or agent.
Mainly, these will be:-
(a)
All
lenses not cleaned.
(b)
Telescope
lighting inadequate.
(c)
All
scales focus properly.
(d)
Horizontal
collimation is within a few seconds.
Any of the above faults should be rectified immediately they
cannot be done under field conditions.
3.1.2 The
minor adjustments which can be done are :
(a)
Adjustment
of tension of slow motion and footscrews with the capstan bar provided.
(b)
Centralising
the plate bubble, if badly off centre. This is done by levelling the instrument
inside a screen (or in the shade), then bringing the plate bubble close to the
central position, with a capstan bar. This is not a precise adjustment as the
bubble will almost certainly move off a little, during the season.
(c)
Adjustment
of vertical collimation : This is done by reading a FL and FR vertical angle to
a prominent point. If these 2 angles agree within a few seconds, no adjustment
is necessary. If not, mean the FL and FR angles to get the true vertical angle
to the prominent point. Then proceed as follows :
(i)
Lay on
prominent point, clamping lightly both horizontal and vertical circles.
(ii) With alidade bubble
setting screw, set the vertical circle to read the true vertical angle. While
doing so, notice that the bubble ends, as viewed through the prism, will move
apart.
(iii) Using the screw provided
for adjusting the Alidade bubble, the ends of this bubble are brought into
co-incidence, as viewed through the prism, and the adjusting screw is locked.
The vertical circle has now had the collimation error eliminated.
It is advisable to again read the FL and FR vertical angles to check that the
adjustment has been successful.
(d)
The
lighting set should be checked, by the observer prior to the commencement of
the season. See all connections are clean and firmly soldered, and the rheostat
free from rust. If it is not allowed to get wet, the lighting set should give
no trouble during the season. Power supply is three, 1.5 volt dry cells coupled
in series, and packed in a plywood box. The rheostat should be turned well down
while the dry cells are new.
(e)
Maintenance.
Keep the theodolite clean, and all parts free from dust, at all times. Use a
camel hairbrush and lens tissues, also cover the instrument with a plastic bag,
when set up and not in use.
3.1.3 Tripod
This should be re-varnished at the end of each field season, and
left stored with all bolts slackened, in case humidity expands the timber.
Before again using the tripod, check that all bolts are tight, and that there
is no movement at any point where the timber fits into any metal socket, either
at the head or foot, of the tripod. This should be done each day the instrument
is used, particularly if the weather is getting drier and hotter. The tripod
should be wrapped in hessian or canvas for vehicle transport.
3.2.1 Setting up the instrument
The tripod should be set over the station or eccentric mark so
that the height is just right for the observer; no straining because it is too
high, and no excessive stooping because it is too low. However; it is better a
little low, than too high.
When the instrument is too high, there is a tendency to drag it
off level; or to fail to get rid of parallax, owing to the eye not being
directly behind the telescope. If azimuths are to be observed as well, the
tripod must be oriented so that the instrument can be set up with two
footscrews along a north south line.
Once the tripod has been positioned, pegs should be driven if at
all possible. 450mm x 75mm square wooden pegs on firm soil, 1 metre x 75mm
square for sandhills, or 300mm to 450mm steel pegs on rocky hills. If unable to
drive in all pegs, put in as many as possible. Set feet in plaster of paris
(use plenty) where pegs cannot be driven. See that when driving pegs, the
tripod has not become displaced from its original position, tilting the head
badly from the horizontal, and displacing the centre of the tripod from a
position vertically over the mark, thus making it impossible to plumb the
instrument accurately over the mark, without overhanging the tripod head.
Spend some time in clearing the observing platform of rocks,
either loose or partly buried; stamp near each leg, and check for any slight
movement of the instrument or tripod. Remember that a partly buried rock, well
clear of the tripod, may touch other buried rocks, which in turn, do touch the
tripod feet.
3.2.2 Observing
screens
This is set up to give plenty of room to move around the
instrument; see that the screen poles are not on line to the distant stations;
and star, if azimuth is to be observed.
3.2.3 Levelling
the Wild T2 theodolite for second order observations
This is done in two
stages:-
(a)
Fairly
accurately, with the plate bubble.
(b)
Final
accurate levelling with the alidade (split) bubble.
Stage (a):-
Firstly, bring the plate bubble along the line of two foot-screws,
and note the position of one end of the bubble, say the vertical circle end.
See Figure 3.2.3(a) Turn through 180°, note the position of the same end of the
bubble. (Figure 3.2.3(b)) Correct by half the difference of these positions,
turn through 180°, until the bubble is level over the two foot-screws. Then
turn through 90°, where the bubble will be in line with the remaining
footscrew; Figure 3.2.3(c) shows this position. Use the same method to level
the instrument along this line, with the single footscrew, this time.
Stage (b):-
Now bring the alidade bubble along the line of two footscrews,
bring the bubble ends, as seen through the prism, into coincidence, and turn
the theodolite through 180°. Note the amount of
error. Take half out with footscrews, and half with the alidade screw. Turn
instrument through 180°, and repeat until level along the line of these two
footscrews. Now turn through 90°,
so bubble is aligned over the remaining footscrew, bring bubble into
coincidence, turn through 180°, note amount of error, take
half out with remaining footscrew and half with alidade screw. Turn through
180°, and repeat until level along the line of this footscrew. The instrument
is now completely level. When shielded properly from the sun, and strong winds,
the Wild T2 will hold the level for long periods. It should be remembered to
position the footscrews approximately centrally, before commencing levelling.
3.3.1 Horizontal and Vertical scales
While it is not difficult to focus the telescope and scales, great
care must be taken, or the observations will be below standard. Remember, as
all observers eyes are different, no one else can help by checking your focus.
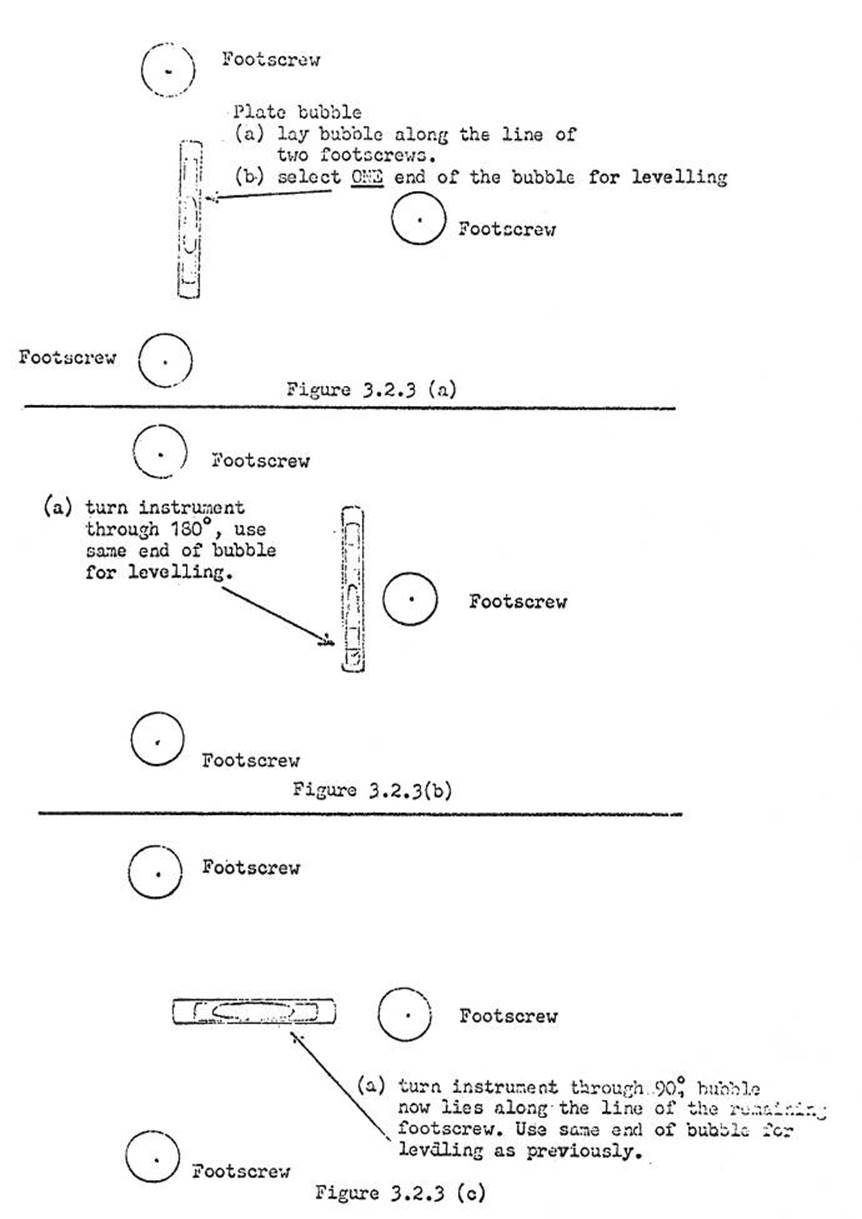
The telescope:‑
(a)
Elevate
the telescope to the sky, and bring the crosshairs to the clearest and sharpest
focus obtainable, by turning the ocular focusing lens.
(b)
Sight
distant station through the telescope, and focus until the distant station is
also clear and sharp.
Move the eye around, when both crosshairs and the distant station
are in focus, there will be no relative movement (parallax) between them. Once
it is dark, and the light is turned on, in the telescope, invariably, both the
distant station, and cross-hairs will need re-focusing.
The scales:-
Always use the lighting set to illuminate the scales (except for
reference mark work, around the station.) Carefully focus the scales until the
figures are sharp and clear. There may be a slight difference in focus between
the horizontal and vertical scales but this rarely matters.
3.3.2 Types
of horizontal and vertical scales
The following is an explanation of the Wild T2 theodolite scales
these being the instrument mostly in use. However, the observer need only to
master the technique of reading the Wild system, to easily change to whichever
Wild theodolite is at hand.
3.3.3 Horizontal
Circle
This is graduated to 20 minutes, and the 10 minute is found by
interpolation. The micrometer drum is graduated to 1 second, with a run of 10
minutes. Looking into the scale telescope, two windows are seen. In the top
window, by means of prisms, two diametrically opposite sections of the horizontal
circle are seen, one the correct way up, and the other upside down. An index
line is shown in the centre of the scale. In the bottom window, a section of
the minute and second scale, with index line, is seen.
3.3.4 Reading
the horizontal circle
When the micrometer drum is turned, the minutes and seconds will
move past their index line, and the opposite sections of the horizontal circle,
will move so that the graduations appear to approach one another movement of
the micrometer drum is continued until the equivalent graduations of the
horizontal circle are brought into coincidence. Now the index line, in the
upper window, will either coincide with a graduation mark, or will come
half-way between two. In the former case, the degrees and minutes are read
direct, using the 20 minute mark which coincides with the index mark; in the
latter case, interpolate to the ten minute lying between the two 20 minute
marks. The reading on the micrometer scale gives the number of minutes and
seconds to be added to the degrees, and tens of minutes, read on the main
scale. Figure 3.3.4 shows an example, and mentions an alternative method of
ascertaining the value of the divisions.
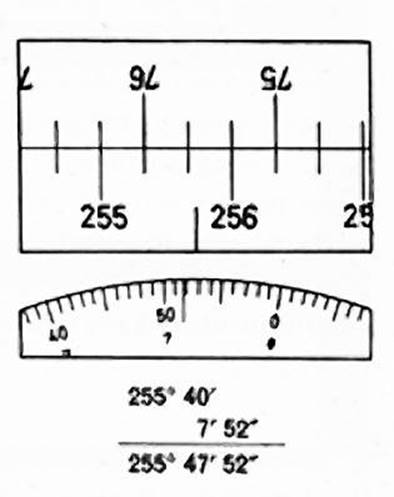
Figure
3.3.4. Horizontal circle
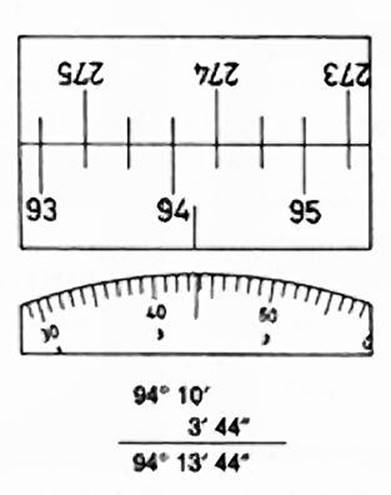
Figure
3.3.5. Vertical circle reading on one face only.
Figure 3.3.4. shows the image in the reading microscope eyepiece
after coincidence. In the upper window, the index line shows the approximate
value will be close to 256° and the first upright figure left of the index
line, shows a reading of 255°. Now count the intervals from 255° to the
diametrically opposite 75° mark. There are 4 intervals, that is, four tens of
minutes, or 40'. A reading of 255° 40' is thus obtained from the upper image.
In the lower image of the seconds drum scale, we read 7 minutes and 51.8
seconds. Thus shown on the drum, the complete reading is 255° 47' 52", the
nearest second always being recorded.
3.3.5 Vertical
circle
The vertical circle on the Wild T2 is graduated similarly to the
horizontal circle. However, it should be noted that on FL it reads ZENITH
DISTANCE, and on FR, 180° plus the zenith distance.
As the altitude is normally the vertical angle required (however
the Sun azimuth proforma uses the zenith distance) it will be necessary to make
the following calculations:-
Face left :
If the observed angle is less than 90°, take it from 90°, and the answer is a FL angle of Elevation.
If the observed angle is more than 90°, take 90° from it, and the
answer is a FL angle of Depression.
Face right :
If the observed angle is more than 270°, take 270° from it, and
the answer is a FR angle of Elevation.
If the observed angle is less than 270°, take it from 270°, and
the answer is a FR angle of Depression.
The mean of the FL and FR
angles gives the altitude free from collimation.
3.3.6 Reading
the Vertical Circle
The graduations are read in exactly the same manner as with the
horizontal circle, with the exception that immediately before the graduations
are brought into co-incidence, the two ends of the alidade bubble, as viewed
through the prism, must be brought into coincidence. The horizontal cross-hair
has been set exactly on the aiming point, and the alidade bubble ends brought
into coincidence with the tangent screw. Then the diametrically opposite
graduations of the vertical circle are brought into coincidence, by turning the
micrometer drum.
The reading from the upper
window is : 94° 10¢
and from the lower window : 03¢ 43.8²
Thus the full reading
(always to nearest second) : 94° 13¢ 44"
3.4.1 Observing
The following method of observing horizontal angles (most of which
also applies to observing azimuths) has been designed so that all movement
becomes automatic, and the hands always go to the right control on the
instrument, whether in daylight or darkness. Also, to eliminate errors, which
could result from friction, or any slight wear of the instrument. Once the
technique is mastered, the observer should work quickly, and smoothly, acquire
a very light touch on the instrument, move quickly, but carefully, around the
instrument. It should be turned with two hands, one lightly holding each
standard, not by the end of the telescope.
Targets normally will be either opaque beacons, helio's, lights
either in daylight or immediately after dark.
Observations will be made in the last couple of hours of daylight
or immediately after dark. In theodolite and tellurometer traversing generally
only two distant stations will be observed.
3.4.2 Double
pointing system
Most time is consumed in locating each distant station, and the
greatest source of error in observing, is pointing at these targets, therefore,
once the target is located, much greater accuracy is obtained if two distinctly
different pointings are made, the micrometer drum being read at each pointing.
This method is known as double pointing.
Before commencing observing, see that both horizontal and vertical
slow motion screws are centrally positioned, to ensure an equal amount of
movement, in both directions.
The rear station of the direction of advance of the traverse will
normally be the reference object (R.O.), so that any traverse angle shown in
the field book; will be the clockwise angle from the rear to forward station.
On face left, bring this target between the double wires, set about 30" on
the micrometer drum, and with the circle setting knob, set the circle to 00°
00'.
The instrument is now
ready to commence observations, proceed as follows:-
(a)
Face
left, swing left through 360° until the R.O. is close to the cross wires in the
telescope, clamp the instrument, and bring the target centrally within the
double wires, (fairly close to the horizontal wire) using the horizontal slow
motion screw and making the last movement of this screw, a "screwing in”
motion against the spring. Bring the scales into coincidence with the
micrometer drum, the last movement of which should also be "screwing
in". Read the angle, move the cross wires clear of the target with the
slow motion screw, and again centralize the target within the double wires,
once again making the last movement of the screw, as previously. (This movement
of "screwing in" the slow motion screw is most importnat to keep
tension against the spring. Remember also that when the instrument is on face
right, the screw is on the opposite side of the theodolite to the observer,
therefore, great care must be taken by the observer to ensure he still uses the
"screwing in" motion on this face). Bring the scales into coincidence
and read the angle. If the pointings are over 3" apart, discard both, and
take two more. If still wide apart, the focus is probably incorrect, on either
telescope or scale, or both. If the focus of the instrument is satisfactory,
conditions must still be unsatisfactory for observing.
(b)
Unclamp
the theodolite, swing left until the distant station is close to the vertical
cross wires (and about a similar distance from the horizontal cross wire, as
was the R.O.). Repeat exactly as in (a). If the instrument is swung too far
past the station to lay on the target with the slow motion screw, continue the
swing, in the same direction, through 360°.
(c)
Unclamp
the theodolite, change to face right, swing right until the same station is
close to the cross wires, clamp, and repeat as in (a).
(d)
Unclamp
the theodolite, swing right, until the R.O. is close to the cross wires, and
repeat as in (a). That completes the observations on this scale setting.
(e)
Set
micrometer drum to 03¢ 50", set scale to
required setting with circle setting knob (in this case 240° 00'). Swing right through 360° and bring target centrally between the double wires, as
previously explained. Continue observing in this manner, until 6 arcs, which
comprise one set, are completed.
3.4.3 Scale
settings
|
|
1st Set
|
|
3rd Set
|
|
5th Set
|
|
FL
|
000°
|
00'
|
30"
|
|
15°
|
001
|
|
|
20°
|
00'
|
30"
|
|
FR
|
180°
|
00'
|
30"
|
|
195°
|
00'
|
30"
|
|
200°
|
00'
|
30"
|
|
FR
|
240°
|
03'
|
50"
|
|
255°
|
03'
|
50"
|
|
260°
|
03'
|
50"
|
|
FL
|
60°
|
03'
|
50"
|
|
75°
|
03'
|
50"
|
|
80°
|
03'
|
50"
|
|
FL
|
120°
|
07'
|
10"
|
|
135°
|
07'
|
10"
|
|
140°
|
07'
|
10"
|
|
FR
|
300°
|
07'
|
10"
|
|
315°
|
07'
|
10"
|
|
320°
|
07'
|
10"
|
|
|
|
|
2nd
Set
|
|
4th Set
|
|
6th Set
|
|
FR
|
210°
|
02'
|
10"
|
|
225°
|
02'
|
10"
|
|
230°
|
02'
|
10"
|
|
FL
|
30°
|
02
|
10"
|
|
45°
|
02'
|
10"
|
|
50°
|
02
|
10"
|
|
FL
|
90°
|
05'
|
30"
|
|
105°
|
05'
|
30"
|
|
110°
|
05'
|
30"
|
|
FR
|
270°
|
05¢
|
30"
|
|
285°
|
0.5'
|
30"
|
|
290°
|
05¢
|
30"
|
|
FR
|
330°
|
08¢
|
50"
|
|
347°
|
09'
|
55"
|
random
|
350°
|
08¢
|
50"
|
|
FL
|
150°
|
08'
|
50"
|
|
167°
|
09'
|
55"
|
arcs
|
170°
|
08'
|
50"
|
Settings are slightly
approximate.
Naturally, on return to
the R.O., collimation will give some variation to the original settings.
Each of the above sets is meaned, and normally, at least 4 to 6
sets are observed.
Usually, the range in each set is about 5", with an odd arc
to 7" or 8"; however, if conditions are difficult, this range may not
be achieved. Once the observer is experienced, and carefully and
conscientiously observes the targets, and scales, as he sees them, the spread
in the arcs is really a measure of the observing conditions. Thus results below
standard, by an experienced observer, would indicate the need to re-observe
that station under better observing conditions.
3.4.4 Check
or random arcs
From a random, initial setting on the R.O. in any one of the sets,
two arcs are read just as carefully, in the normal manner, to the distant
station. This is to ensure that the degrees and minutes, have not been read
consistently wrong. The usual care in reading those arcs, is required so that
they can be used in the set. There is such a short period of good visibility each
evening that full advantage must be taken of it.
3.4.5 Booking
horizontal angles
The booker will record the name and/or number of each station
observed, also the type of target observed. The observer will call out the
degrees and minutes, a slight pause during which the booker calls back the
degrees and minutes. The observer, who has read the micrometer drum, for the
first pointing, during the pause, calls out the "seconds" reading;
points again, and calls out the "seconds" reading, once again. The
booker calls back these readings, as he records them.
All calling out should be
sharp and business-like.
The booker should mean the two seconds readings, and subtract the
mean reading on the R.O. from the mean reading on the distant station, as the
observations are being taken, meaning these answers at the bottom of the page,
when the set is completed. See example Figure 3.4.5(a).
At the conclusion of the night's observations, the observer will
check all reductions and the means of the sets. Both booker and observer will
sign each page. The observer should cover the previous answer with scribbling
paper, while he completes his checking, to get a completely independent answer.
3.4.6 Vertical
Angles
These will be truly simultaneous, and should be read between 1400
hours and 1600 hours LMT (Local Mean Time), when the air is most evenly heated.
However, if lines are less than 16 Km (10 miles) in length, they may be
observed between 1000 & 1700 hours, but still must be observed
simultaneously. Lines less than 3km (2 miles) in length may be read
non-simultaneously.
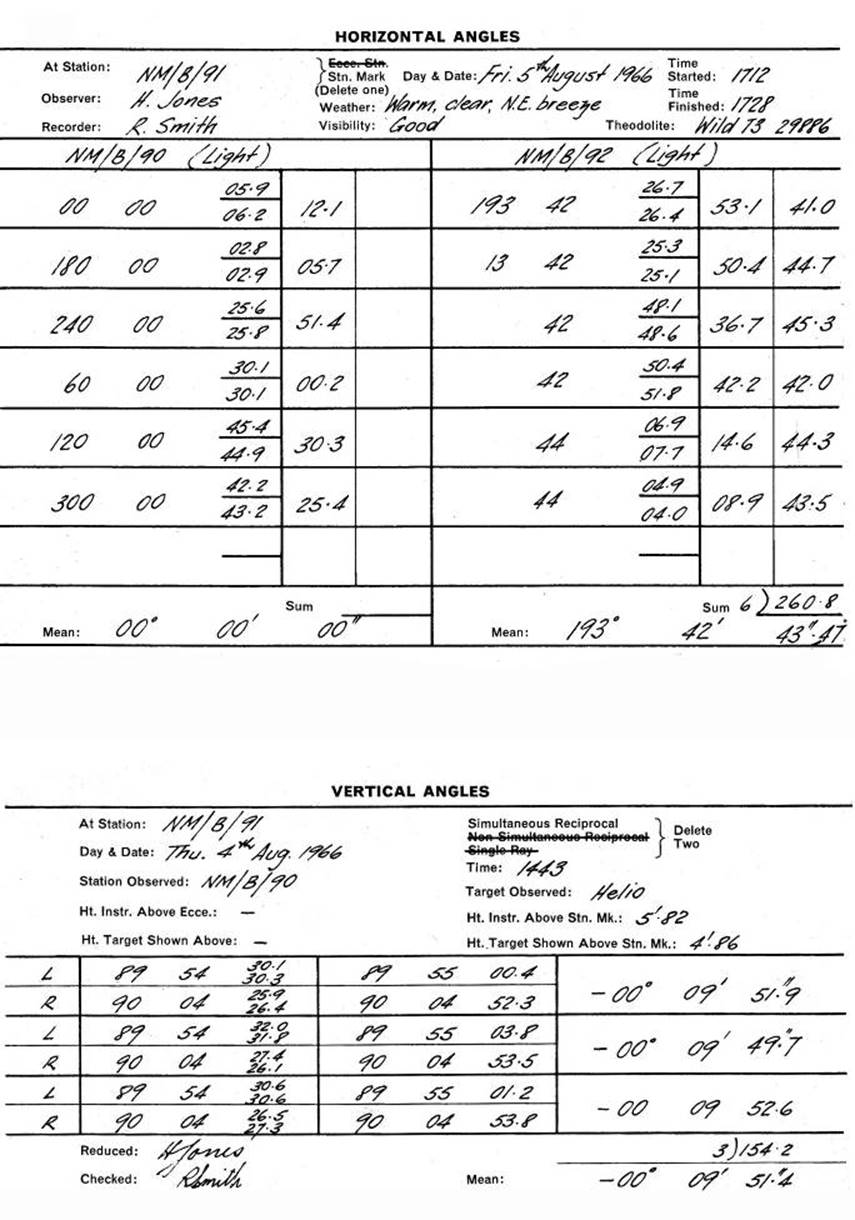
Figure
3.4.5(a) – Booking Horizontal Angles and Figure 3.4.10(a) - Booking Vertical
Angles.
3.4.7 Probably the
best type of target over the average length of line is a hello, and for shorter
lines, the daylight (Flamethrower) lamp. The top of the vanes makes a fair
target on lines up to 32km (20 miles) in length, if the lines have a good drop
away at each end. Heights of targets above a station mark (or below, in rare
cases) must always be recorded.
3.4.8 Screens should
always be used for vertical angles; normally at the time of observation the sun
will be beating strongly on both the instrument and tripod, unless they are
shielded. If conditions are not too windy, and the time is short, a makeshift
shelter which completely shades the instrument and tripod will suffice; i.e.
the vehicle and part of the observing screen, or swag cover, etc.
3.4.9 Observing
technique
A similar system of double pointing to that used for observing
horizontal angles, is used for observing vertical angles. To keep in line with
this system, it is essential that the alidade bubble ends are brought into
coincidence just prior to each reading of the micrometer drum, even though the
ends appear to still be in coincidence from the previous reading. This helps to
even out erroneous readings arising from "flat" spots in the grinding
of the level vial.
Observing procedure:-
(a)
Face
left, intersect the target with the horizontal cross wire close to the central
vertical wire, making the last movement of the slow motion screw against the
spring, i.e. "screwing in".
(b)
Bring
the alidade bubble ends into coincidence, in the same manner, read the
graduations on the scale, Move the alidade bubble slightly off, move horizontal
cross wire slightly off, then intersect the target once again exactly as
before, again bring the bubble ends into coincidence, and again read the
graduations on the scale.
(c)
Change
to Face right, and repeat as above. The difference between the readings
obtained on these faces, is the vertical angle, and 3 such angles make up a
set. To be sure of best results, the observer must change face after each pair
of double pointings.
3.4.10 Booking
vertical angles
On face left, after pointing on distant station, and levelling
alidade bubble, the observer will call out the degrees and minutes, a slight
pause during which the booker calls back the degrees and minutes. The observer,
who has read the micrometer drum for the first pointing, during the pause,
calls the "seconds" reading, points, and levels the alidade bubble
again, then calls out the “second” once more. The booker calls back the
readings as he records them, and should mean the seconds readings, bringing the
Face Left angle forward, into the next column to the right, in the field book.
The observer changes to Face Right, and both observer and booker, repeat the
above. The booker means the FL and FR vertical angles, and brings the resultant
answer forward to the last column on the right, in the field book. When three
such angles have been obtained, the set is complete, and the mean is brought
down to the bottom of the page. Measure and record, heights of instrument and
targets above station mark. See Figure 3.4.10(a) for an example.
The observer will check the reductions, and both will sign each
page. The booker should check that there is no gross error, in the degrees and
minutes, while the observation is in progress, by noting the approximate total
of the readings on both faces. This should be about 360°, unless the instrument
is badly out of adjustment.
3.5 Measuring
and Recording Reference Marks, Eccentric Stations, and Recovery Marks
(This section is to be read in conjunction with 1. Chaining and 7.
Station Marking)
The normal method adopted
for measuring reference marks, has been to set a theodolite over the station
mark (if accessible) or if not, an eccentric mark, and measure all distances by
vertical angle and slope distances. Horizontal angles related to a distant
station, and the station mark where applicable) are also observed. As marks are
usually within 4 to 10 metres, the tops of hills rough with large boulders, and
generally windy conditions prevail, the above method has been found to be more
accurate than horizontal measuring with tape and plumbobs. If time permits, set
up over a second mark, so that all distances can be checked by calculation.
If time is short, measure
tie distances, horizontally with tape and plumbobs, and check slope distances
by direct horizontal measurement. There should always be three reference marks.
It is impossible to cover
all problems which will be encountered at the various types of set ups, however
the following three will cover most cases.
3.5.1 Where
the station mark is accessible
Set the theodolite over the station mark. Lay on a distant station
as RO, and set 00°00'05" approximately on the horizontal scale. Read
horizontal and vertical angles to each mark on FL. Change to FR and do the
same, but this time, measure slope distances, while laid on each RM. Measure
height of instrument above station mark.
If plenty of time, set theodolite over one of the RMs and with
00°00' 05" on the scale, lay on the station mark, read horizontal and
vertical angles to the station mark and RMs on FL; change face, read angles and
measure slope distances and height of instrument. See figure 3.5.1(a).
If time is short, measure tie distances horizontally with tape and
plumbobs. See figure 3.5.1(b).
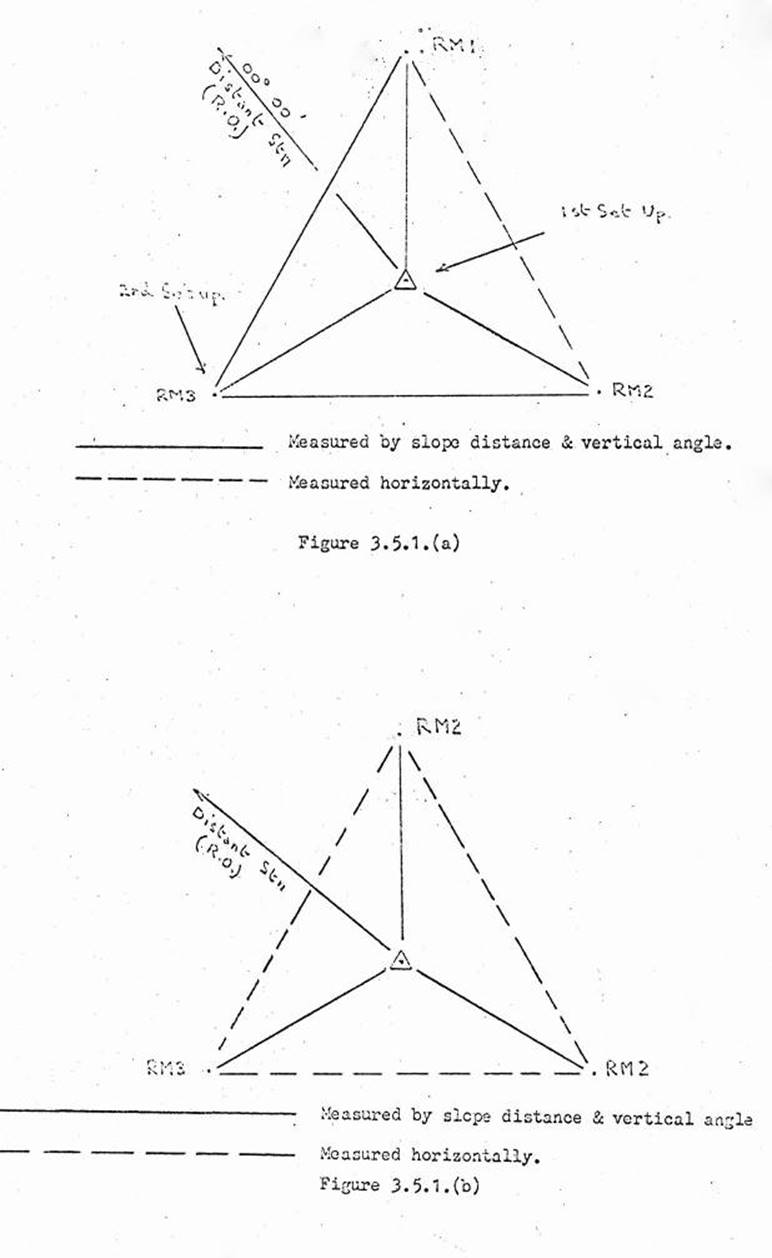
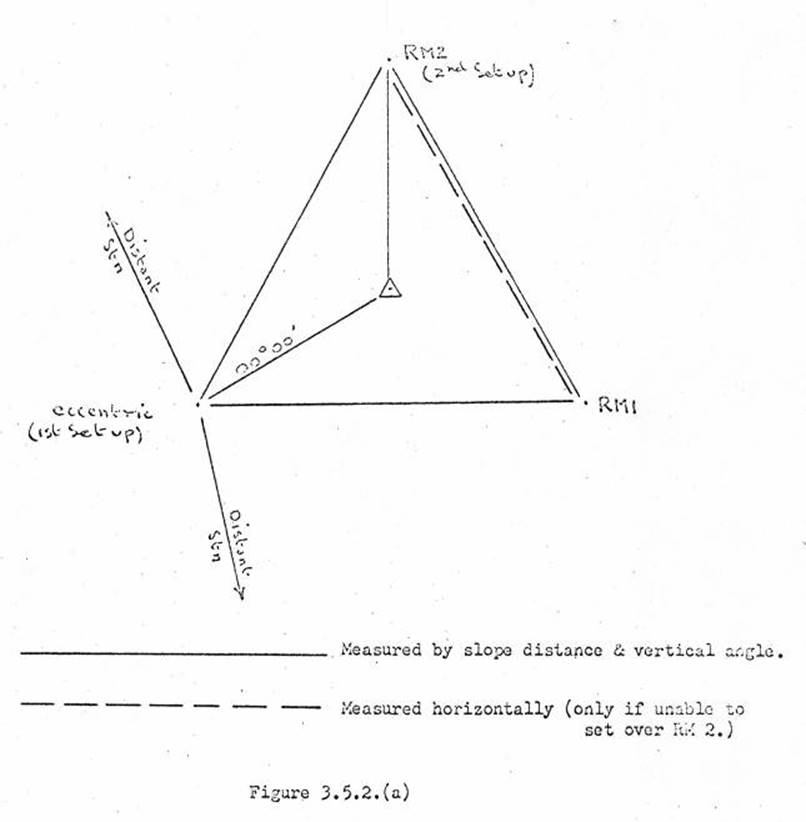
3.5.2 Where
the station mark is inaccessible
This will normally be where a large cairn with pole and vanes,
covers the station mark. If this is a new station, the distance, eccentric mark
to station mark, will have been measured by the beaconing party, as will also
the horizontal angles to the two RMs. This data must be with the observer who
will lay on the centre pin on top of the beacon with 00°00'05" set on the
horizontal scale. Read horizontal and vertical angles to the station and
reference marks. Also measure height of instrument, slope distances, cut in at
least one of the distant stations. The observer will check against the data
supplied, for gross error in the original work of the beaconing party wherever
possible, also set up over an RM, and read horizontal and vertical angles to
the station mark, eccentric mark and the other RM, on both faces of course.
Measure the remaining distance horizontally. See figure 3.5.2(a).
3.5.3 Where
there is a distant recovery mark
(This section should be read
in conjunction with 7.2.3)
This type of mark will only be placed where the station mark is
likely to be lost, either permanently or temporarily i.e. on a sandridge which
may erode, swampy & ground or tidal flats. When the above conditions occur,
a substantial recovery mark (or marks) will be placed on the nearest firm
ground.
Set up the theodolite over the station mark, lay on a distant RO,
and set 00°00'05" approximately on the horizontal scale. Read horizontal
and vertical angles to the recovery mark, and the two base terminals.
Set over the recovery marks and the two base terminals, in turn,
reading all horizontal and vertical angles, thus closing both triangles. Be
sure to measure all the heights of instruments, and heights of targets. These
observations must be done in good visibility. Targets must be carefully
plumbed, and very small; i.e. tripods with plumbobs (laying on plumbob string
near hook). If care is taken, the triangles will close within about 10" to
20". Each, almost exact, 100 metre base line is to be measured twice (with
an invar tape, if possible) the tape being laid on the ground, temperature
taken and a pull of 6.800 kg (about 15lb) applied. This must be done in the
very early morning, when the temperature is cool. If a 50 metre band is used, pull
will need only to be about 4.600kg (10lb).
Figure 3.5.3 shows a typical Recovery Mark and base line. In 7.2.3
the preparation of the base line, and the Recovery Mark, are described.
All angles are read, so that distance, Station Mark to Recovery
Mark, can be calculated from each triangle.
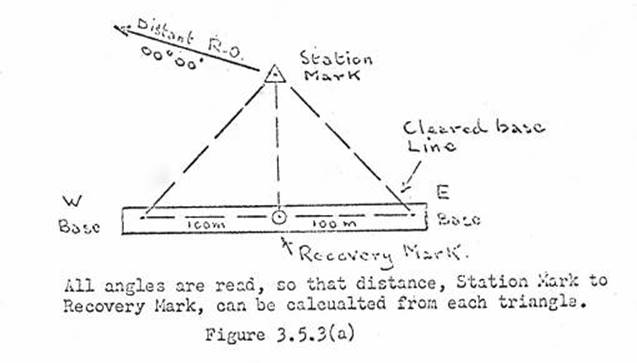
3.5.4 Reference
Mark measuring
Figure 3.5.4(a) gives an example of measuring from 2 different set
ups. The station mark is covered by a large cairn. Pages, appropriately ruled,
are provided in the Traverse, Trig., and Azimuth field books for this purpose.
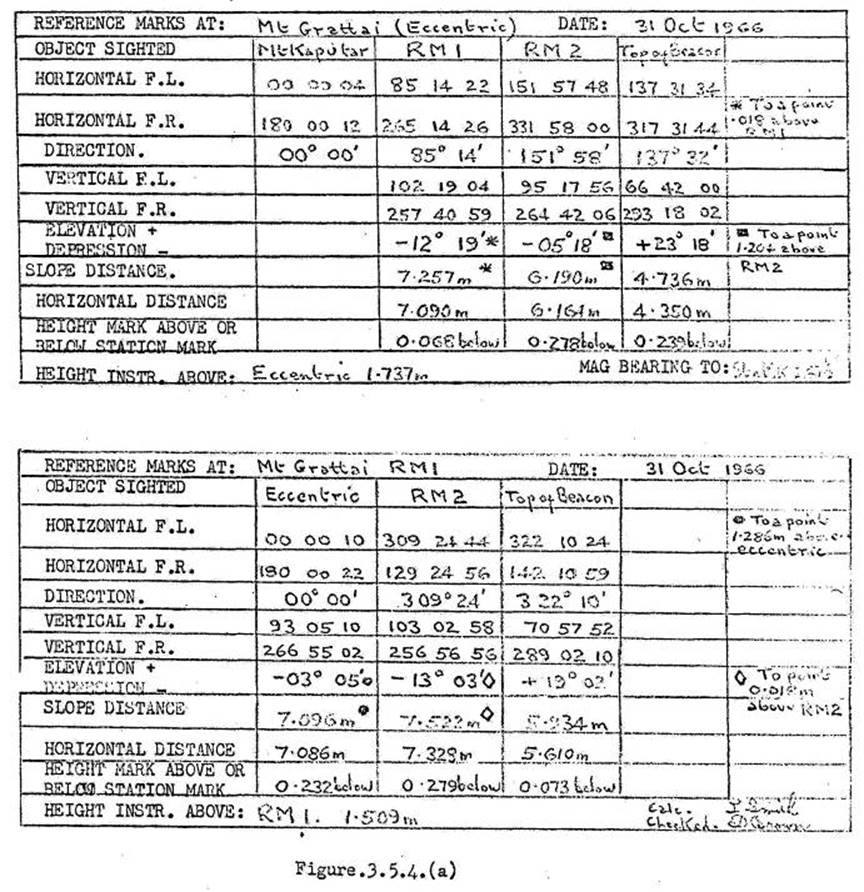
3.5.5 Computation
of Reference Marks
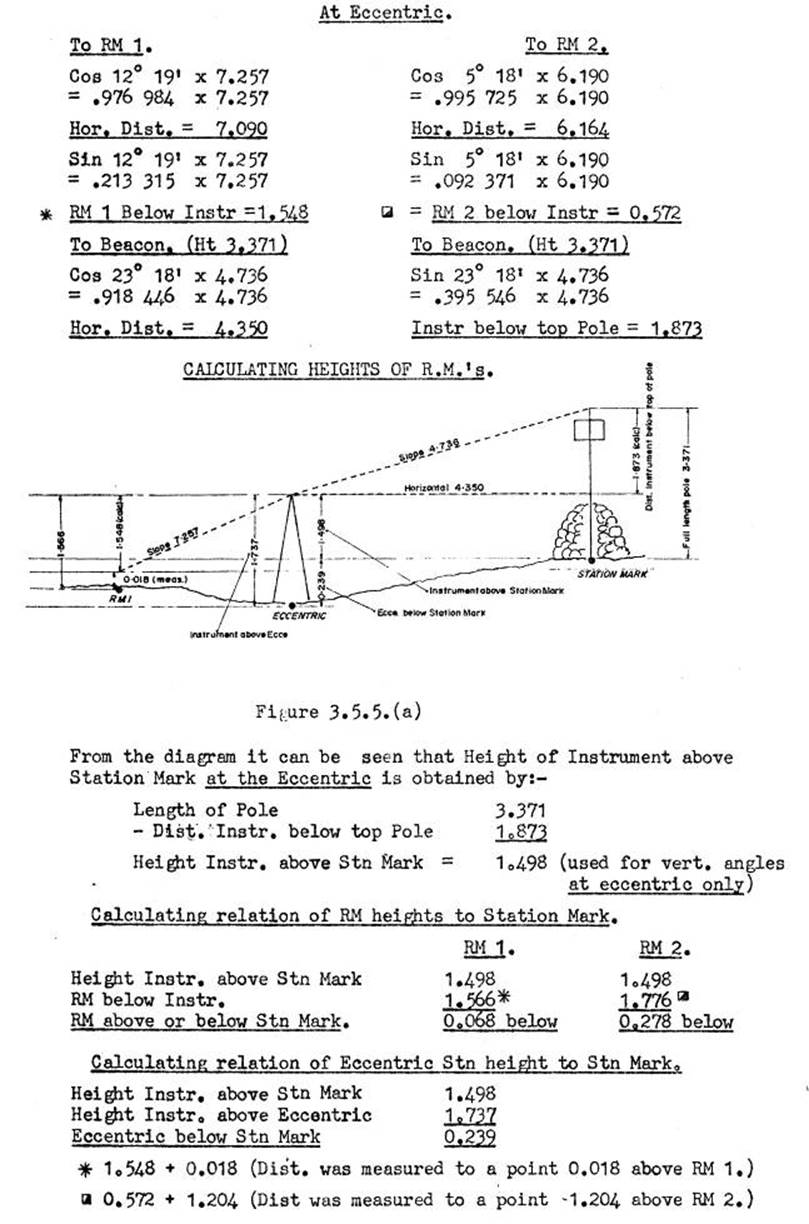
Where the theodolite has been set over two reference marks, all
distances can be checked by simple calculation using the formula:-
a/Sin A = b/Sin B = c/Sin C
See Figures 3.5.5(c) and
3.5.5(d) for examples.
Where only two sides, and the included angle are known, the
remaining sides and angles can be calculated, as shown on the proforma Figure
3.5.5(e). Where Measurements have been made twice, they should normally agree
within 3 to 4mm. If over 6mm measure again. Calculated checks should also have
about the same agreement, if the triangles formed, are reasonably well shaped.
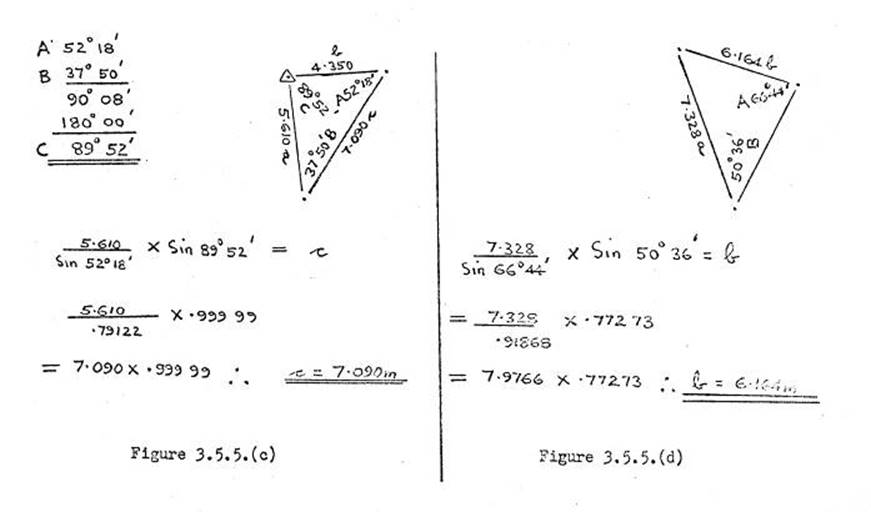

3.6 Eccentric Corrections
3.6.1 Formula
Eccentric corrections, which many find difficult to understand,
are really quite simple, once the principle is grasped.
The Sine formula is used:—
a/Sin A = b/Sin B = c/Sin
C
The distance, Eccentric Station to Station Mark, is required, also
the angle (at the eccentric) between the Station Mark and the Distant
Station(s).
The distance to each distant station is required. This does not
have to be exact; thus distance, eccentric to eccentric as measured by the
tellurometer is quite accurate enough.
3.6.2 Computation
In Figure 3.6.2(a), the bearing, or direction, we have is from the
eccentric to the distant station, and we need the correction to apply to it, to
get the bearing from the station mark to the distant station. The broken line,
from the station mark has been drawn parallel with the line, eccentric to
distant station therefore, it is on the same bearing.
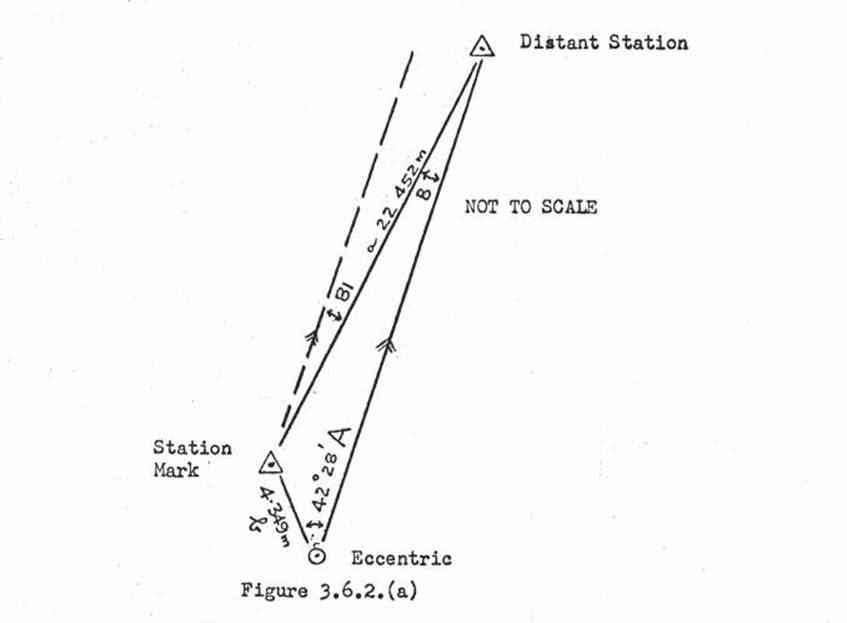
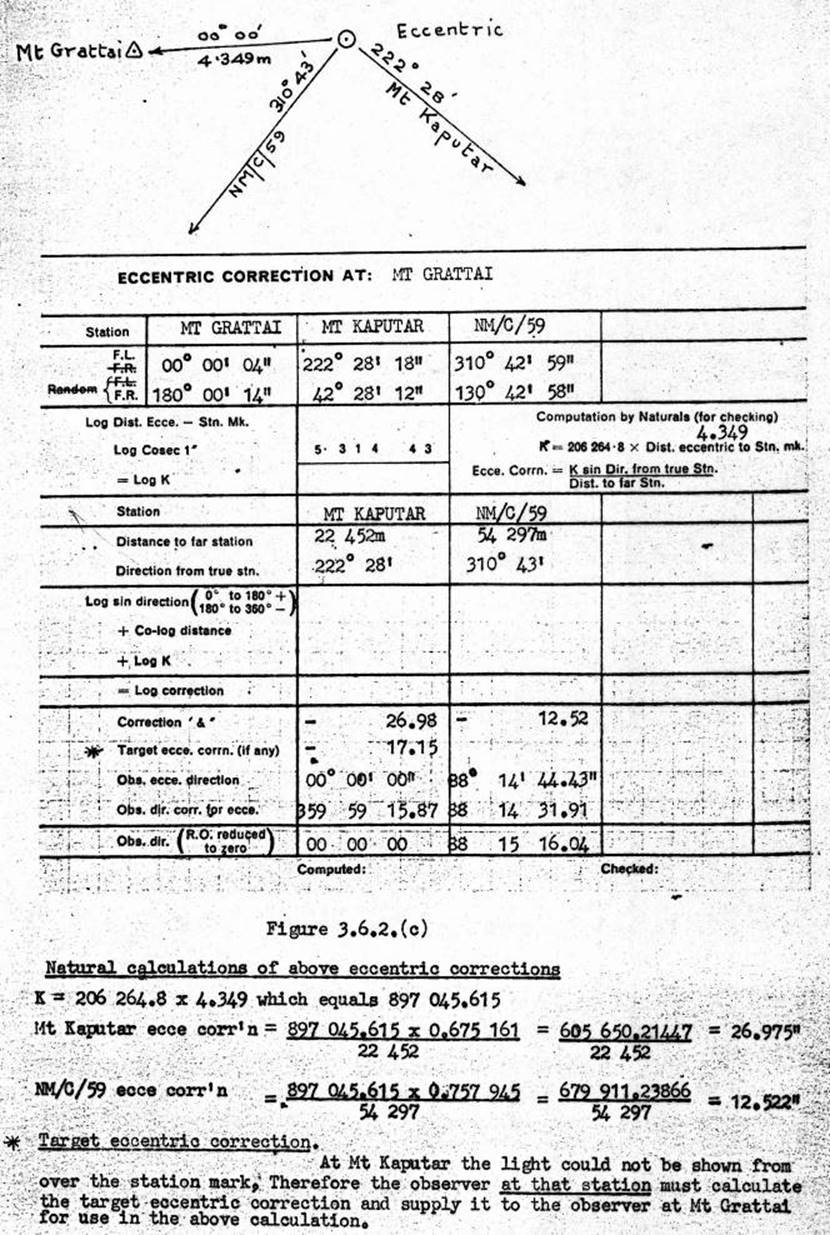
The eccentric correction
is the angle B1, and, as the bearing is greater, the sign is +.
B1 is the same value as B,
therefore the calculation is:-
a 22 452 = b 4.349
Sin A 42º 28’ Sin B
Or
Sin B = Sin 42º 28’ x
4.349 / 22 452
Log 4.349 0.638
39
Log Sin 42º 28’ 9.829 41
Sum 0.467 80
Log 22 452 - 4.351 26
Log Sin Ecce C'n 6.116
54 (between 26 & 27 seconds)
+ 5.314 43 (Log Cosec
1")(*)
Log Ecce C’n 1.430
97 (in seconds)
Ecce C'n +
26.98"
(*) This is applied so that the angle can be looked up as a direct
logarithm (rule for small angles; Chambers Tables).
The above formula is used in the proforma in the field book.
However, to avoid subtractions, in the calculation, the Co-log of the distance,
Station Mark to Distant Station, is used; and the Cosec 1" is added to the
distance between Eccentric and the Station Mark, to give Log "K", and
save 1 line in the main addition.
It should be noted, where the angle at the eccentric station,
between the Station Mark and the Distant Station is under 180°, the correction
is plus, and where the angle is more than 180°, the correction is minus. If in
doubt, draw a thumb-nail sketch. See Figure 3.6.2(b) for an example of an
eccentric correction, worked out on a proforma.
3.6.3 Small
corrections to observations where target at the Distant Station is slightly off
line.
The following plotted
method is normally used where targets are eccentric by small amounts only, up to
1 metre. If care is taken it is quite accurate. It is also a valuable check for
gross error in ordinary eccentric corrections:-
(a)
Plot
station "A" (Station where target is eccentric) with ray to station
"B" (Station where observations are being made to "A"). Use
magnetic bearing for plotting this ray which is not to any scale. Note distance
to nearest Kilometre against this ray.
(b)
At a
suitable scale, plot eccentric target by magnetic bearing and distance, which
should be in mm.
(c)
It is
necessary to find the distance that the target is off line, at right angles
to the ray, "A" to "B".
(d)
The
eccentric correction will be the amount this distance subtends at the distance
between stations. Use the close approximation that 1 second of arc = 5mm per
Kilometre.
(e)
The 2
examples below show the two types of plot required to cover all situations.
(f)
It is
easy to decide, by inspection of the plot, whether the direction observed is
too great or too small, and thus give the corrections its appropriate sign.
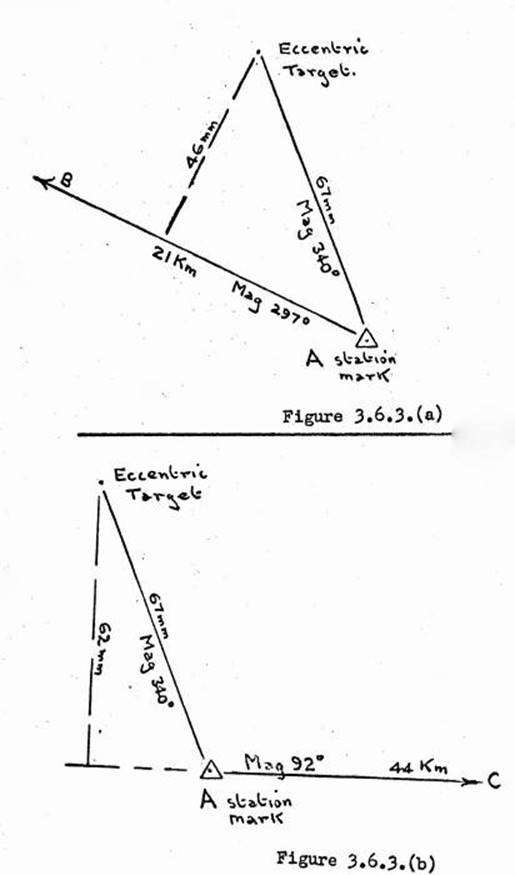
Refer Figure 3.6.3(a) : Target
is eccentric by 67mm on a Mag. Bearing of 340°. This gives a distance off line
of 46mm from plot.
Calculation:- 5mm x 21km
gives 105mm per sec at 21km. Correction is 46mm, which means correction in
seconds will be about 0.5" or 105/46 = 0.44".
Looking in from B it is
seen that the bearing observed is too small, therefore correction is plus.
Refer Figure 3.6.3(b) : Same target is sighted from C. This gives
a distance off line of 62mm from plot. Note that ray A to C has to be extended to
measure right angle distance which target is off line.
Calculation:- 5mm x 44Km
gives 220mm per sec at 44 Km. Correction is 62mm, which means the correction in
seconds will be about 0.3² or 220/62 = 0.28"
Looking in from C, it is
seen that the bearing observed, is too large, therefore the correction is
minus.
3.6.4
To
ascertain amount of lean on a pole, the base of which is a cairn
(a)
Mark a
line around the pole, 1 metre, or some other suitable distance, from the top.
(b)
Stand
about 7 metres from the cairn, and at right angles to a face of the pole, point
"A" in the diagram 3.6.4(a).
(c)
With
plumbob, sight edge of pole at "X", and mark x vertically above, on
the top edge of the pole. If greater accuracy is required, use the theodolite,
instead of the plumbob. Measure distance from corner of pole C to x. This is
the amount of lean over 1 metre. If this was 20mm, the lean over the full
length of the normal 3.380 metre pole would be:- 20 x (3.38 /1) = 66mm.
(d)
Mark
this distance along the top edge of the pole, from corner C and call it point
“a”.
(e)
From
“a” draw a line across the top of the pole, parallel with the edge.
(f)
Move
around 90° to point B and repeat all in (b), except that the last point to be
marked will be "b".
(g)
The
point where lines "a" and "b" cross, at "c", is
the point where the corner of the pole C would be, if the pole had no lean.
Measure distance "c" to C, and take Mag. Bearing from "c"
to C.
Record that pole leans on
a bearing of ...° for a distance of ...mm.
(h)
From
the centre of the leaning pole at D, mark true centre of pole at "d",
using above bearing and distance. Take all measurements angles to RM's, and
distant stations from point "d".
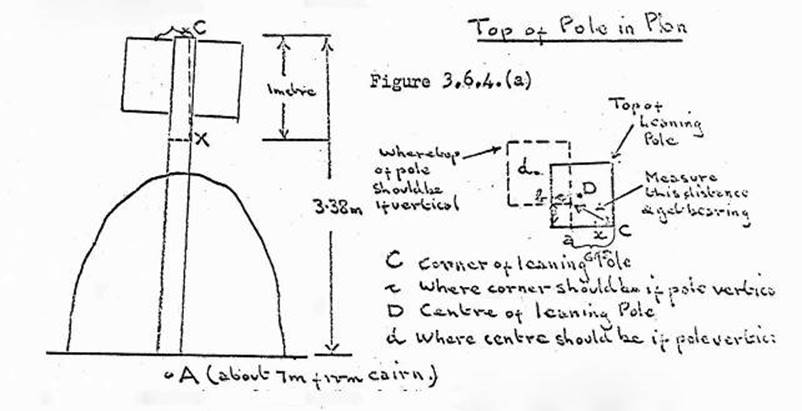
3.7. Plumbing Towers, Tripods and Beacons.
3.7.1. Towers.
These can be plumbed quickly and accurately
over the station mark, with two theodolites. When engaged on tower work, it has
been found necessary to carry an extra theodolite with the party erecting the
towers.
The following
method was adopted:-
See that the adjusting slot on each tower leg
is approximately central on the bolts, so that adequate adjustment is
available.
Set up the two theodolites about 120° apart,
so that they can sight the station mark centrally between two tower feet. They
should be about 30 metres from the tower.
Clear bushes, grass etc., so that the station
mark can be seen - set match in the centre of the mark.
Level the theodolites, lay on station mark
with both instruments and elevate them until they are laid on the tower head.
Look through theodolite No 1 first; loosen
retaining bolts on tower foot opposite No 2 theodolite; move tower until the
theodolite retaining bolt in the tower head, is cut centrally by the vertical
graticule, in the theodolite telescope; tighten retaining bolts on foot
opposite No 2 theodolite.
Look through theodolite No 2; repeat
operation as above this time adjusting with foot opposite No 1 theodolite; as
this is opposite theodolite No 1, this adjustment will not greatly move the
tower off line, from that instrument.
If necessary, readjust for instrument No 1,
tighten retaining bolts and lock. Do likewise for instrument No 2.
Remember all adjustments are done at the foot
opposite the instrument to the one through which the tower head is being
viewed.
3.7.2. Plumbing tripods or beacons.
Tripod, or quadrupod beacons, where the
station mark is accessible would need to be plumbed as in 3.7.1., if
observations are to be done to the vanes.
If observations have already been taken, the
reverse method will have to be used; i.e., lay on centre of vanes from two
positions, depress telescope, and mark plumb point on the ground, near station
mark. Measure distance vanes off line, and take magnetic bearing. Draw plot to
scale, showing the above details; calculate the eccentric correction as in
3.6.3.
Where lights are used and are plumbed over
the station mark, naturally, the above does not apply.
3.8 Sigma Octantis Azimuth determination
3.8.1 Single-ended
azimuth determinations, consisting of one set of 6 rounds, shall be observed on the terminal leg of every spur
traverse, in a
control survey. Additional azimuth determinations may be observed at any stage, to
check the "carried through” geodetic azimuth.
3.8.2 Simultaneous
reciprocal azimuth observations, consisting of two sets, shall be observed on
specified lines, as required. They do not demand exact simultaneity of
pointings by each observer. However, it is important that the two observers, at each end of
the line, commence observing at almost the same time, and finish the two sets,
within 10 minutes or so, of each other.
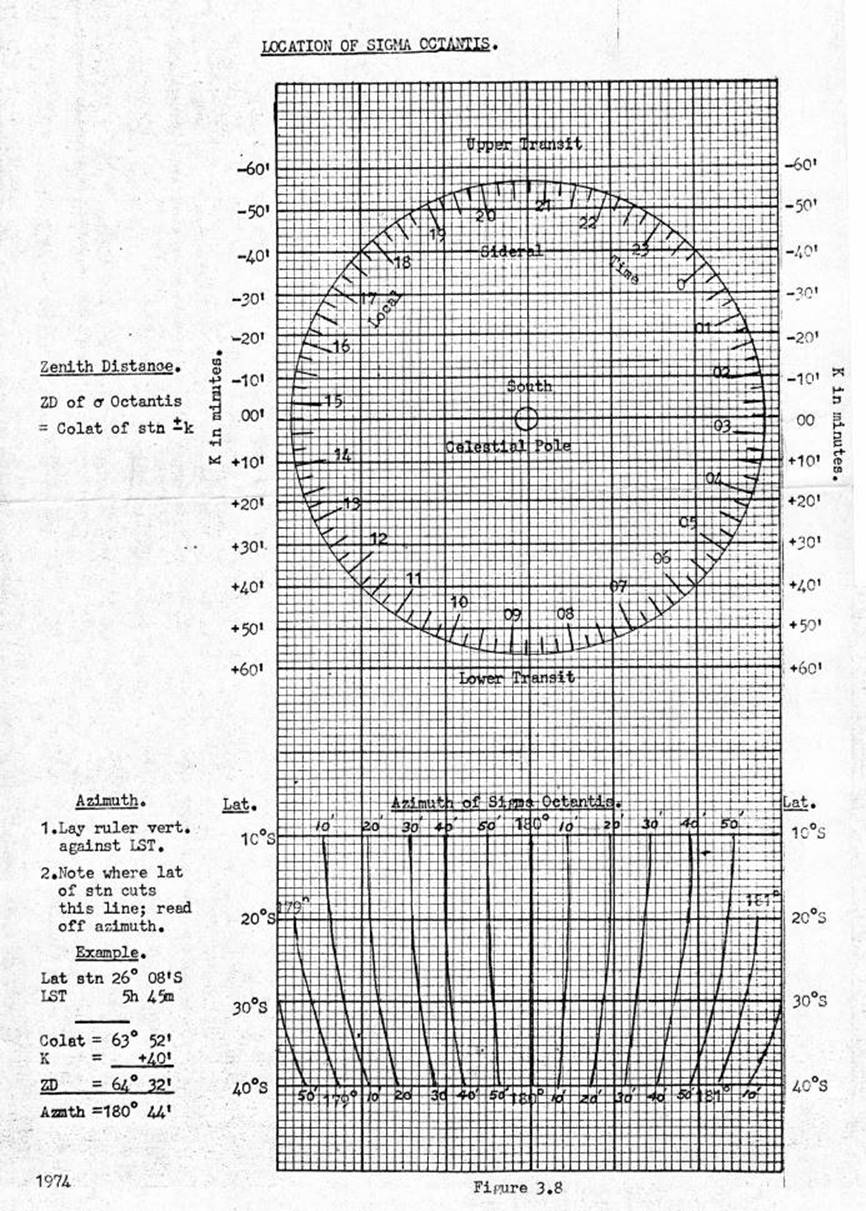
Figure
3.8.8
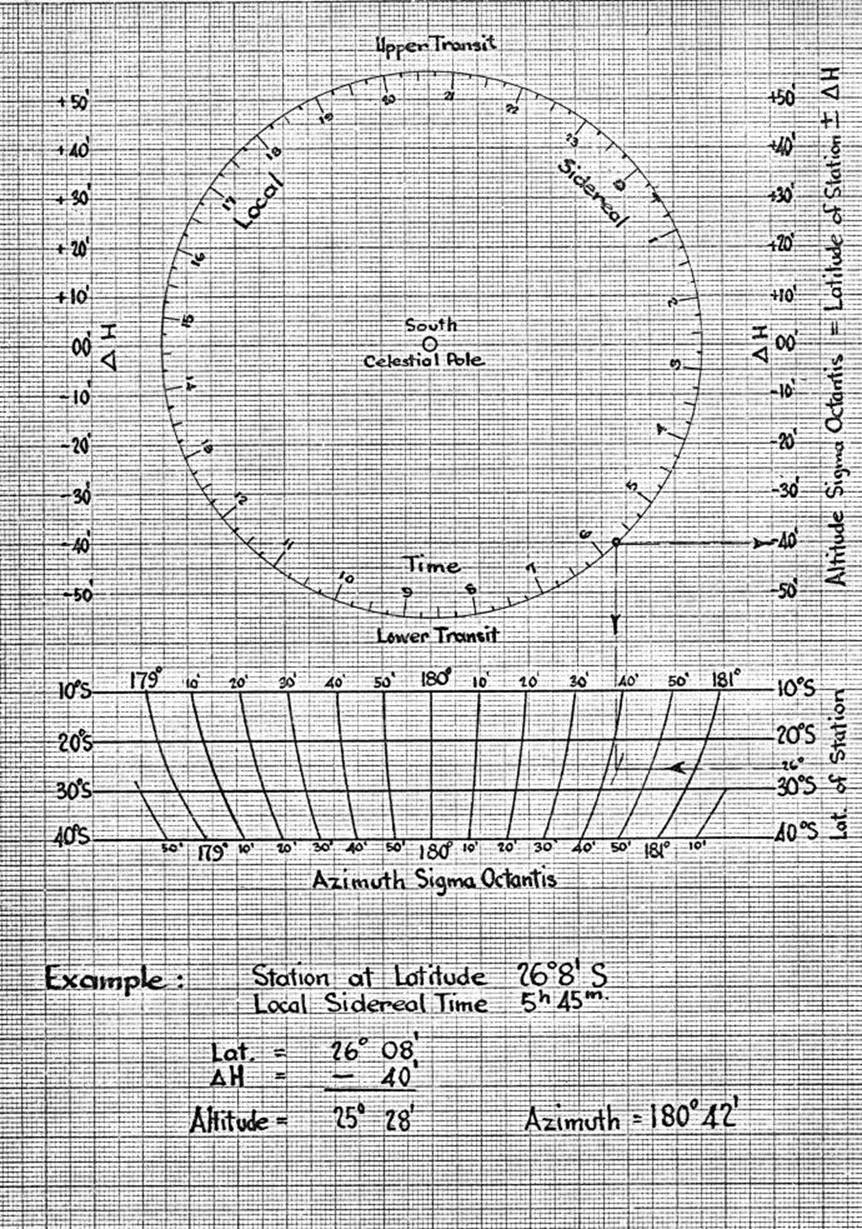
3.8.3 Main equipment necessary
Theodolite and lighting set
Radio, capable
of receiving WWV or VNG.
Split hand stop
watch
Pocket-watch
with second sweep hand.
Observing
screen or tent.
Booking lamp.
Torch (for reading
plate bubble and stop watch.)
Lucas lamp and
battery.
Traeger
Transceiver for inter-communication with distant station.
3.8.4 Time of observation
Observations should commence immediately
after sunset, or as soon as Sigma Octantis is visible. This is the most
accurate period in which to observe, the RO light being at its steadiest at this
time.
3.8.5 Light from RO
A Lucas Lamp, or other suitable light will be
used. It is important, particularly in flat terrain, to keep the lamp as high
above the ground as possible. The lamp should be plumbed over the station mark,
if possible. If observations are also in progress at the station, the light
should be placed exactly on line to the distant station with the theodolite.
3.8.6 Preparations for Azimuth observing
The zenith distance and azimuth of the star,
to the nearest 2 minutes of arc, is calculated for the approximate start time of the
observation. This is done on the graph, Figure 3.8.
Before consulting the graph, it is necessary to calculate the Local
Sidereal Time at which it is desired to commence observations.
To compute Local Sidereal Time :
At NM/E/110 Latitude 26° 08', Longitude 132° 30'
Time, 1950 hours, Central
Australian Time, on 1 March 1970
-west )
L.S.T. = R + U.T. +east ) Longitude
h m
Central Australian Time 19
50 (Time to nearest minute.)
09 30 East of Greenwich
– 09h 30m
Universal time 10
20
R for 10h 20m U.T 10
35 (Pg 6 Star Almanac)
Longitude (East) 08 50 (132.5° Long in time /15)
29 45
-24 00
Therefore L.S.T is 05 45
3.8.8 To
find zenith distance and azimuth of Simga Octantis
Using the computed L.S.T., the graph is used to find DH, and the azimuth of the star.
DH is applied to the
co-latitude, either
positively or
negatively, to give Zenith Distance, depending on whether the star is in upper
or lower transit. In the example the correction is positive. Figure 3.8.8.
3.8.9 Setting
the watches
The pocket watch should be set about 10 seconds fast, on Standard Time. The stop watch should be started
at a suitable time, i.e. if a 30 minute dial, at 00 or 30 minutes, if a 15 minute dial, at
00, 15, 30 or
45 minutes. It should be
started, within 1 or 2 seconds, of the same reading as the pocket watch. This
means that both watches are about 10 seconds fast on Standard Time, and
therefore any errors are more easily detected. The stop watch should be
compared with the
WWVH, WWV, or
VNG time signal, noting the error to the nearest 0.10 second, just prior to the
commencement of the azimuth observations, and also after half the observation has been
completed, and at the conclusion of the observation.
3.8.10 Sequential
Description of the Observing Method
After checking
that the theodolite has been carefully levelled, parallax eliminated, focus
adjusted, and the lighting in the telescope and circles suitable, then:—
(a) With the
theodolite FL, take 2 pointings, and 2 micrometer readings on the RO light, in
the same manner as for horizontal angles.
(b) Set-the zenith
distance, and horizontal angle of the star, as called out by the booker.
(c) Adjust the
vertical pointing of the telescope, so that the star appears just clear of the
horizontal wire, and bring the star centrally between the 2 parallel vertical
wires, calling "up" and pressing the stop watch button at that
instant. On the call "up", the booker records the time indicated by
the pocket watch.
(d) The observer
calls out the stop watch reading, and the plate bubble readings, East and West,
in that order.
(e) The observer
calls out the horizontal circle reading.
(f) Take another
pointing and micrometer reading, again reading the stop watch and plate bubble.
(g) Call out the
horizontal circle reading; on this occasion read the vertical circle to the
nearest minute, and call it out.
(h) Change face on
the star. The booker will call out the vertical and horizontal circle settings,
if desired by the observer.
(i) Take 2 more
pointings and bubble readings, etc., on the star as before.
(j) Take a vertical
circle reading, to the nearest minute of arc, on the star, after the second
pointing.
(k) Swing back on
the RO light and take 2 pointings and micrometer readings. This completes 1
round.
(l) The instrument
should be relevelled after each 3 rounds. However, if at any stage it is
noticed that the instrument is badly off level, it should be relevelled before
commencing the next round from the RO.
(m) When
observations are complete, compare the stop watch readings with the coarse
readings of the pocket watch, looking for 30 second discrepancies. Reduce the
field book as shown in Figures 3.8.10(a) & (b).
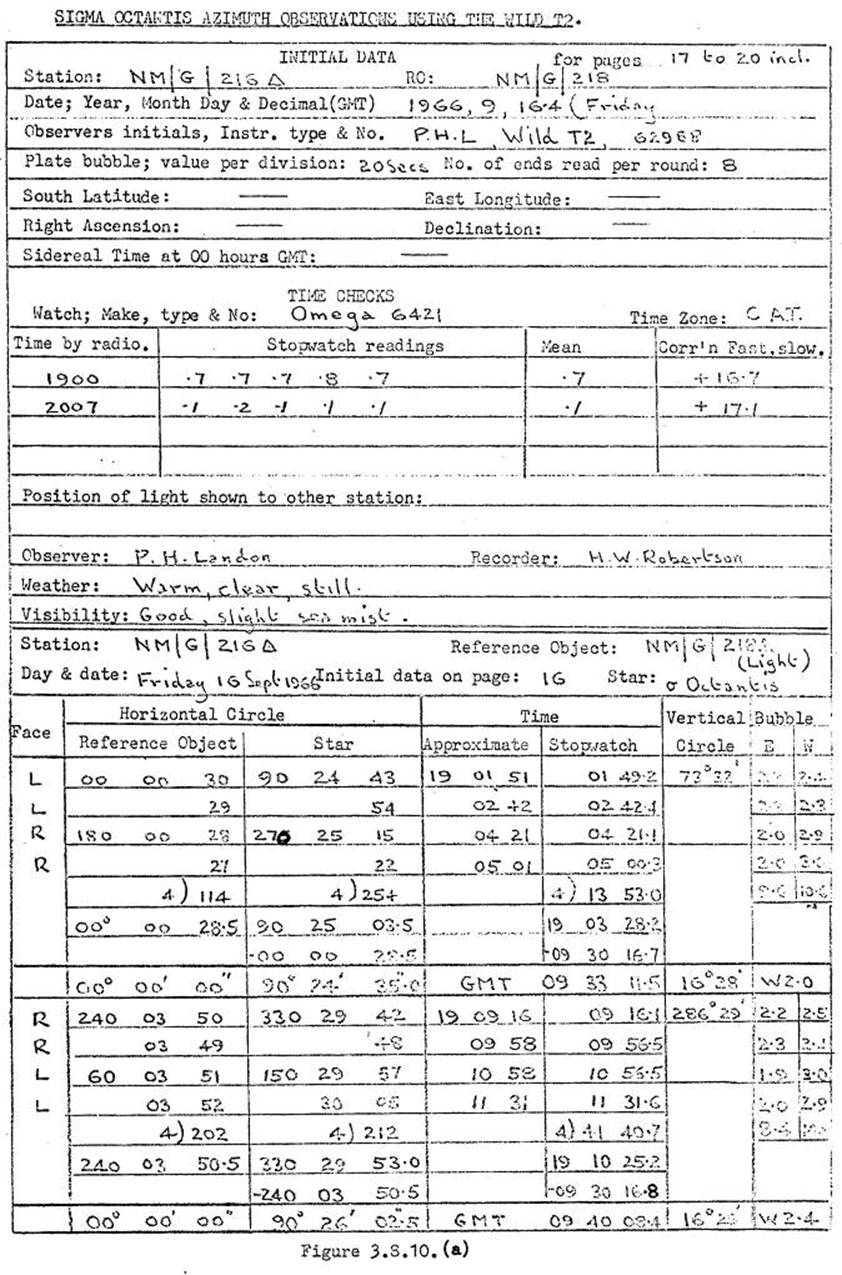
3.9 Hints on Ex-Meridian Sun Observation for Azimuth: Method and Booking.
(a) Time to observe
The best time to observe, i.e. when any error
in Declination, Altitude, or Latitude will have least effect on the computed
result, is when the sun is on or near the Prime Vertical, either East or West,
and at an altitude of 20° to 30°.
However owing
to the sun's path through the changing seasons, it will frequently be
impossible to fulfill the above conditions. For example, in mid-winter, in
Latitude 400 (just south of Victoria), observations between 0930 -
1000 hours, and 1500 - 1530 hours EST will only give altitudes of from 17°
to 21°, and bearings of approximately 40° or 320°
which are well away from the Prime Vertical.
Obviously a
compromise is necessary, and the observer must decide on a time to suit the
time of year and the locality. Luckily, as the observer moves north in
Australia and the Latitude becomes smaller, the conditions for the shape of the
astronomical triangle improve for ex-meridian sun observations.
(b) Observing
technique
As the tabulated values of Declination and
"R" for the sun are referred to its centre, the observations are
arranged in such a way that the mean of the Face Left and Face Right pointings
will give an observation to the sun's centre. Observations are on the limb of
the sun. Remember, in the morning the sun will appear to be descending, and in
the afternoon it will appear to be ascending. Figures 3,9,(a) and (b) show the
technique.
Initial
location of the sun in the telescope.
The sun can blind if the
observer forgets to fit the sun filter to the eyepiece end of the telescope.
To avoid danger from this, the following
method of locating the sun, is recommended:-
(i) Standing beside
the instrument, bring the shadow of the foresight onto the rear sight; lock the
horizontal clamp.
(ii) Hold the palm
of the hand behind the eyepiece, move telescope vertically until the image of
the sun shows on the palm; lock the vertical clamp.
(iii) Immediately,
slip the sun filter onto the eyepiece end of the telescope.
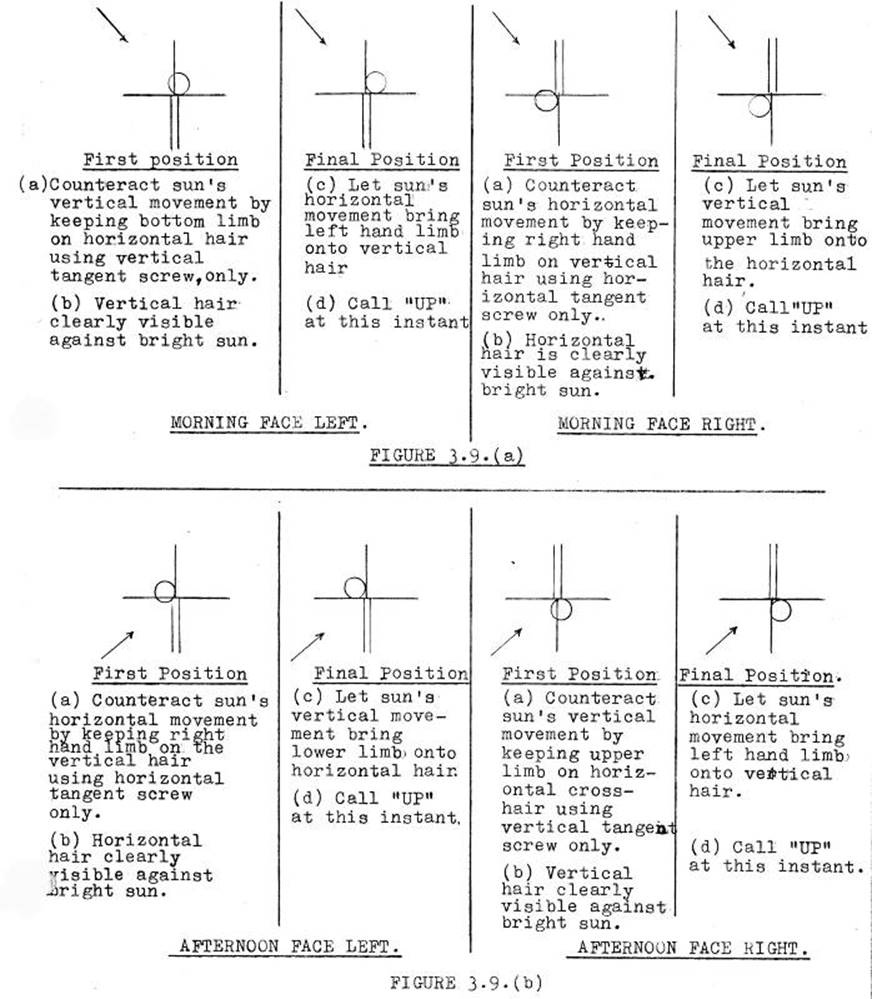
Laying on the
sun
Experience has shown that the best method or
laying on the sun is to use only one tangent screw to keep one limb of the sun
on the appropriate crosshair, letting the sun's own movement bring the other
limb onto its appropriate crosshair. When viewed through the sun filter the
crosshair is only clearly visible against the bright disc of the sun, therefore
the crosshair is initially laid close to the edge of the sun as shown in the
first position in figures 3.9.(a) and (b).
It is then easy to concentrate on the
diminishing-gap between the crosshair and the limb while still keeping the
other limb on its crosshair with the tangent screw. The method can be clearly
seen in the following
(c) Sequence of
observation
FL on RO 00°
00’ 30” approx )
Attach Sun
Filter FL on Sun )
Change face FR
on Sun ) 1 round
Remove Sun
Filter FR on RO 1800 00’ 30” approx )
The second round commences with FR on the RC;
leave scale setting as set, but re-lay on the RO, once again following the
above sequence.
At least 4
rounds, possibly 6, are taken. Figure 3.9.(c) page of F.B.
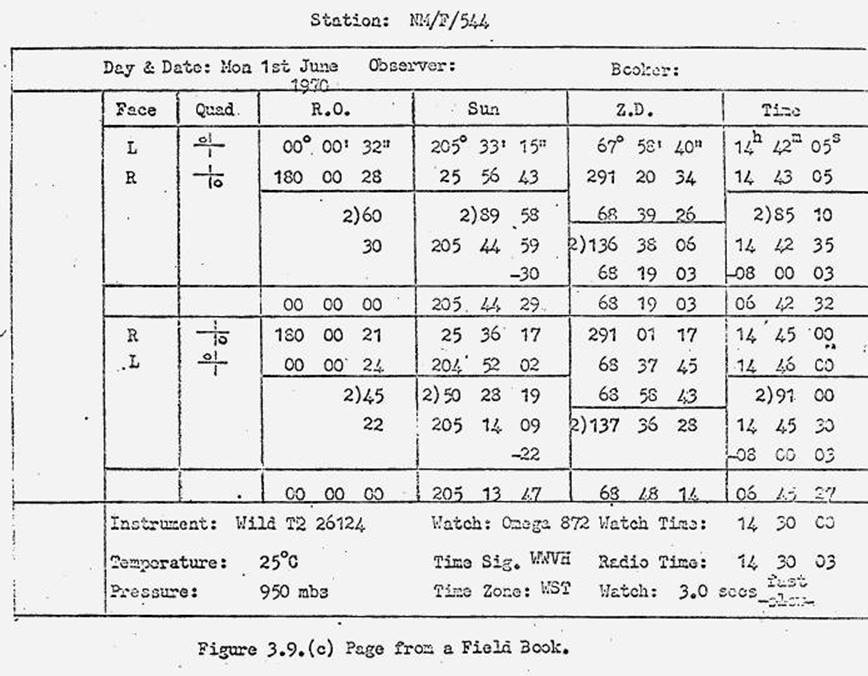
(d) Additional data
required
Time : Should be booked to the nearest second.
Watch should be checked against a radio time signal; correct the booked time,
if necessary.
Temperature & Pressure : Readings should
be taken for use with the Refraction Tables. Those in the Chambers are based on
a standard temperature of 10°C, and a standard pressure of 754mm
(1005.25mbs). Where observations are taken under conditions differing
considerably from standard a noticeable error is introduced if actual
readings or both temperature and pressure are not used in the computation.
Refraction
taken from Chambers is multiplied by:
(Actual
Pressure (millibar) ) * ( 283 )
(1005.25 ) (273
+ Actual T°C )
Refraction increases as pressure increases
BUT decreases as temperature increases.
The back page of the Sun Observation
reduction proforma has refraction and parallax tables for the sun based on
zenith distance.
The Refraction Table is based on 57”*tanZD
The Parallax Table is based on 8.8”*sinZD.
Plate bubble : Usually,with a sun observation
for azimuth, it is not considered necessary to record, and correct for, any
dislevelment shown by the plate bubble. However, it must be emphasised that if
great accuracy is the aim, any dislevelment of the horizontal axis must be
taken into account.
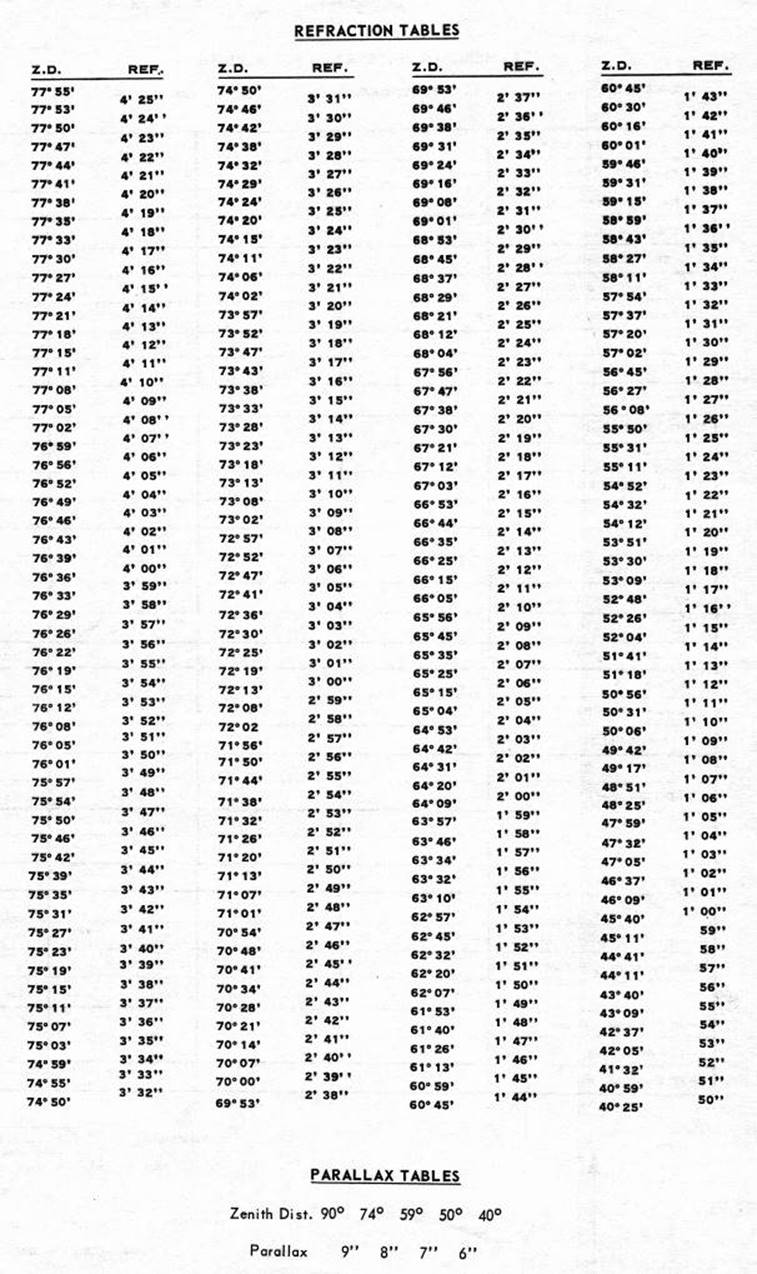
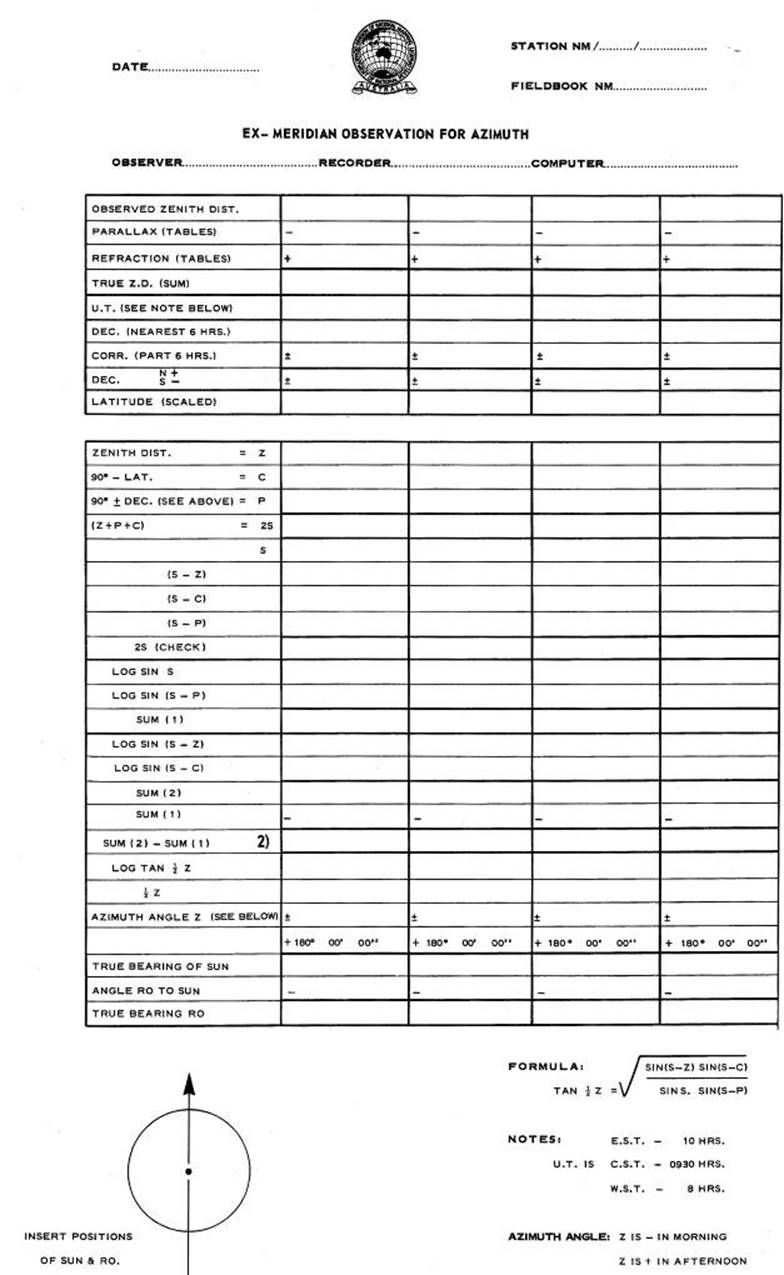
3.9 Sun
observation for Azimuth – Hour Angle and Accurate Time
Traditionally, the method used for observing
the sun for azimuth has been as previously described, i.e., reading
simultaneously the altitude and the horizontal angle to a reference point using
time within one minute. As this method requires no sophisticated equipment and
only an accurate Latitude, it is not surprising that it became the method
almost exclusively used.
The main drawback to this observation is the
limited time each day that the sun is in a suitable position, and the time
necessary for the observer to become proficient in the technique of simultaneously
pointing to both the horizontal and vertical limbs of the sun.
It is pointed out by Dr. G. Bennett of the
University of NSW in an article in "The Australian Surveyor", March
1974, that the Hour Angle method using accurate time is now well worth considering
because:-
(i)
Time signals from VNG should be audible over most parts of Australia during
daylight hours.
(ii) Small
transistor short wave radios for receiving these time signals are readily available.
(iii) Split hand
stopwatches are also readily available.
(iv) Current map
coverage is such that Longitude can now be scaled as accurately as Latitude.
(v)
The method permits the surveyor to take observations over a
greater time range, (even observations at noon, in the winter months should be
quite satisfactory.)
(vi) The observer
has only to concentrate on laying on the vertical limb of the sun and reading
the horizontal angle.
(vii) In an observation where
speed is essential, considerable time is saved in not having to adjust the
alidade bubble and read the vertical angle.
Setting the
watches and Time Signals
The procedure laid down in 3.8.9 should be
followed, however it should be emphasised once again that accurate time is
critical in this observation therefore care must be taken to rhythmically
"beat" the stopwatch in unison with the "beep" of the radio
signal. Beat the finger on the stopwatch button a number of times until this
slight sound is synchronized with the "beep" of the radio time
signal. Once this is achieved press the button on one of the "beeps".
Do not "snatch" at the button on this "beep" or good
synchronisation will be lost; this is a common fault while learning.
The mean of at least five synchronizations
should be taken. Unless cloud causes delay, the sun observation is finalized
quickly; where this is the case a time signal check immediately prior to and
immediately following the observation is sufficient. Where delay occurs take
farther time checks during the waiting period.
Observing and
booking
Reading the stopwatch and recording the
observed data is similar to that of the Sigma Octantis observation for azimuth
except that the plate bubble is not read and no vertical angle is required. As
the altitude of the sun is not observed, temperature and pressure readings are
not required.
The example in Figure 3.9(d) shows the booking method using the
same field book page as for the Sigma Octantis observation. It is advisable for the observer to call
out each vertical limb of the sun as he lays on it; the booker can record this in the Vertical Circle column
as shown. This procedure should ensure that the observer does not forget to
change to the opposite limb of the sun as he changes face. The observation in
the example was done using single pointings, however any observer, once he has attained
sufficient speed, would be advised to use the double pointing method for greater accuracy and less chance of gross error.
The computation of this observation is shown in Figure 12.7(3),
Volume 2 of these notes.
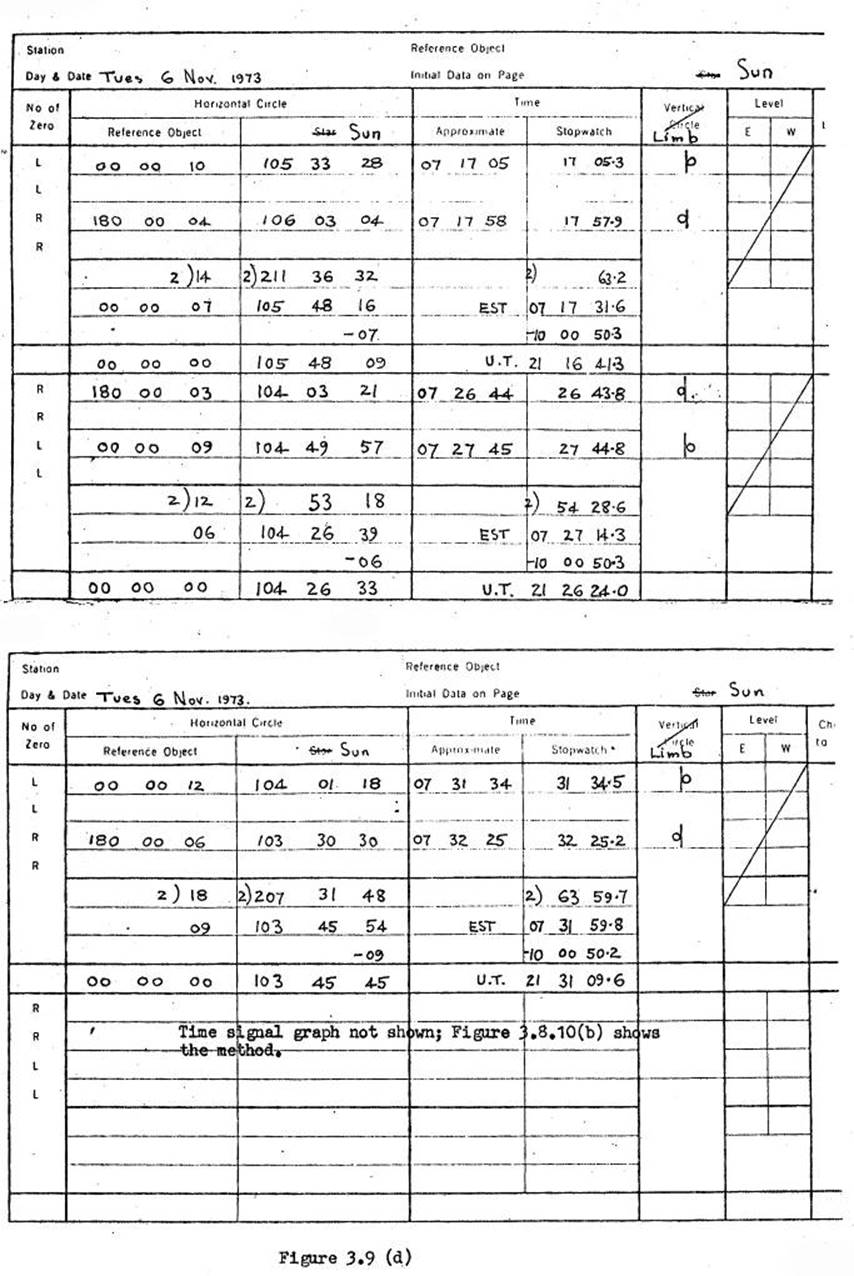
3.10 Meridian
Transit Observations for Latitude & Longitude – Rimington’s Method
A method of astronomical
observations for Latitude & Longitude was needed mainly to provide control
for minor traverses in the N.T. and also the 4 mile map series owing to the
fact that little triangulation control was available at that time (1940-1955).
To make the observation an
economical proposition the requirements were:-
(a)
Observations
for both Latitude & Longitude needed to be done on the one night and take
no more than a couple of hours.
(b)
Field
computations to prove that the result was acceptable had to take no more than
about the same length of time, so that they could be done on the same night or
first thing next morning, to enable the observer to move on (unless, of course,
the computations indicated further observations were necessary).
After considerable research, the following method was evolved by
Mr. G.R.L. Rimington. His paper in the Australian Surveyor, combines a
description of the method and the calculations necessary, with the historical
background of the first trial observations.
The following is a brief
description; this is then amplified in a "step by step" procedure.
(i)
A
programme of stars is prepared.
(ii) Theodolite is laid out on
a N-S line, stars are paired alternatively N & S, or vice versa.
(iii) The accurate time and
"rate” of the chronometer is found; it is advisable, but not necessary,
for the chronometer to be slightly fast, and it is probably best set on the
standard time of whichever Australian Time Zone the observer is in. However, it
can be set on GMT (UT), if preferred.
(iv) Longitude observation.
Using the "early stadia" wire, the star is timed on FR by stopwatch
and chronometer prior to its reaching the centre wire (the meridian), and timed
again, this time on FL as it reaches the same "offset" wire, now termed
"late stadia". From this it can be seen that the star is not timed as
it crosses the meridian, the time that this actually took place being the mean
of the "early" and "late" stadia times.
(v)
Latitude
observation. As the star crosses the meridian (centre wire) on FL, the vertical
angle is read. This is the Z.D. with the Wild T2.
(vi) The above procedure is
repeated with a star in the opposite direction to give a "pair".
Computation of this pair will give both a Latitude and Longitude of the
position.
The observation needs no
elaborate equipment; the main requirements are :
(i)
Theodolite,
Wild T2, or similar, with Talcott Bubble if possible. Also lighting set,
prismatic eyepieces and tripod. The instrument to read to one second, the
telescope to elevate to about 70°, and to have two, "offset" vertical
hairs. The instrument selected was the Wild T2, and the two "offset"
vertical hairs were placed at the same distance L & R of the centre
vertical wire as the normal stadia wires are above and below the horizontal wire,
i.e., about 17 minutes of arc. Thus the names "early Stadia" and
"late Stadia" have been adopted for these two hairs. See Figure
3.10(a).
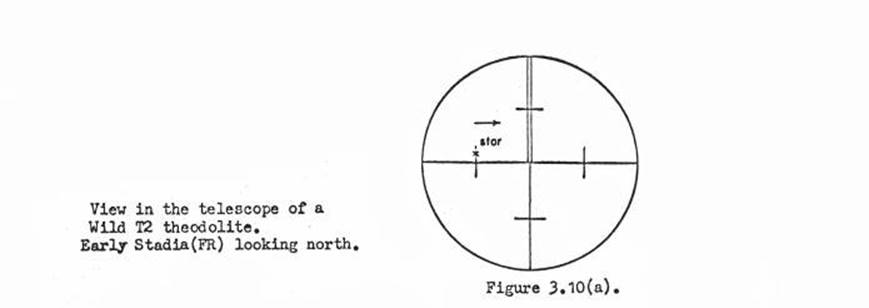
(ii) Surveyor’s or ship's
chronometer, half second beat. Good stopwatch reading to one-tenth of a second,
with wide enough graduations to estimate to one-hundredth of a second,
pocket-watch.
(iii) Apparent Places of
Fundamental Stars (FK4), star programmes, Sigma Octantis graph, field books, maps,
etc.
(iv) Table and light for
booker, thermometer.
(v)
Observing
pegs for theodolite tripod.
For this observation there are four
main steps :
(i)
Office
preparation of a star programme and the Sigma Octantis graph.
(ii) Field preparations before
dark
(iii) The actual observation
after dark.
(iv) The field computation
before leaving the station.
Step 1 Office preparations
(a)
Programme
of stars
Once the general area for the field work is known a programme of
stars is prepared for the Mid-Latitude of that area. A long list of suitable
stars is extracted from the FK4. They are listed as North or South, Name,
Magnification, RA & Dec, and columns are left in which to enter (360°-ZD)
and ZD, on arrival at the place where the observation is to take place.
The RA is not listed as such but as "Early Stadia", and
a time allowance of approximately two minutes to the RA is made to allow for
the difference in time between the stars arrival on the "Early
Stadia" and its arrival on the centre wire (the meridian).
As the North stars move a lot faster than the South stars, it is worth
calculating this time allowance for both North & South stars of a suitable
ZD for observing. This can be done thus:‑
The value of the space between the stadia Wires is 1:100 which is
34' of arc (2.26 minutes of time). Thus from a stadia wire to the centre wire
as 17' of arc (1.13 minutes of time).
This time interval x Secant Declination of the star gives the time
the star will take to travel from the stadia to the centre wire, (or stadia to
stadia, if required).
A North star with a Sec. Dec. of 1.0610 x 1.13min = 1.20min.
Therefore "Early Stadia" for this star is RA -1.20min, allow 2min.
A South
star with a Sec. Dec. of 2.0050 x 1.13min = 2.26min. Therefore "Early
Stadia" for this star is RA-2.26min, allow 3min.
The above figures are approximate only; as no correction has been
made for Latitude, they apply to a point on the Equator.
This can be used also to check doubtful observations, and is an
indication of the time available for changing face and reading the ZD as the
star crosses the centre wire. When checking doubtful observations always allow
for the Latitude.
Diagrams for 30° South
Latitude

|
(i) Star
with Nth Dec. of 12° would have a ZD of 30° + 12° = 42°. It would be to the
observers north and would be O.K.
|
Stars in the shaded area are unsuitable, thus
stars with North Dec. of 0° to 20° & South Dec. of 0° to 10° are suitable
North stars. Stars with a South Dec. between 50° & 80°, are suitable
South stars
|
|
(ii) Star with a Sth Dec. of 55° would have a ZD of 55° - 30°
= 25°. It would be to the observers south and would be O.K.
|
In selecting stars for the programme, list those between about 1.0
and 6.0 magnitude. Use in the observation, wherever possible, those between 2.5
and 5.5. As the Wild T2 will only elevate to about 70 (20° ZD) and because of
greater unreliability of refraction in lower altitudes, stars with a ZD over 50° should not be selected, another limitation is placed on the stars
which can be entered in the programme. Draw rough diagrams as in Figures
3.10(b) & 3.10(c) to give a clear picture of the stars which can be selected.
The selected stars for a six to seven months observing season
cover about three foolscap pages and will be useable for some years. Sufficient
copies to permit the using of one programme per station should be made
available to each observer.
A computer programme is now available to select stars for such a
season’s work.
(b)
Graph
for the location of Sigma Octantis
A graph giving the ZD and Azimuth of Sigma Octantis at any LST at
the Equator should be made.
For the accuracy required there is no need to solve the
astronomical triangle; just use a series of plane triangles with the hour angle
each half hour between 0hr and 06hrs and the hypotenuse the CO - ZD (Polar
Distance). Thus the Polar Distance x sine hour angle gives the Azimuth
correction, and the Polar Distance x cosine hour angle gives the ZD. See Figure
3.10(d).
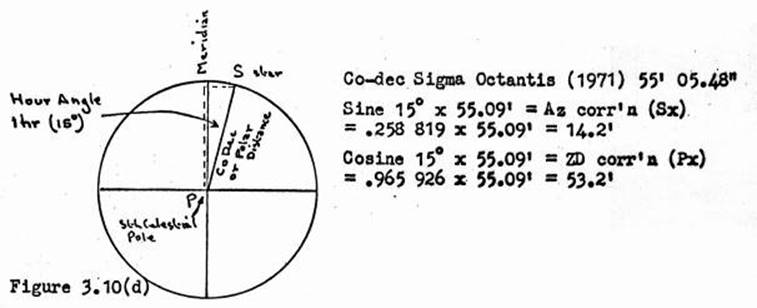
As the RA of the star is the LST when the star is on the meridian,
this is the start point for the graph, points are plotted to obtain both ZD and
Azimuth curves for each half hour from this start point. Thus in 1971, with the
RA and Dec. of Sigma Octantis 20h 40m 04.36s and S89° 04' 05.48² respectively, 10 right angled triangles with the hour angle each
half hour (in arc 7.5°) increasing from 7.5° to 82.5°, and with the hypotenuse (Co-dec.) a constant, can be quickly solved
on a calculating machine. Signs for these corrections are indicated in Figure
3.10(e).
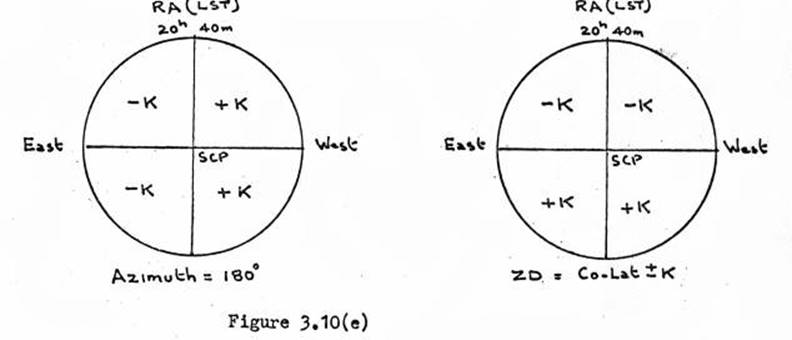
There is a slight variation in the movement of Sigma Octantis from
year to year; while this is not sufficient to cause trouble in locating the
star, if it is required to use the graph to lay out on a reasonably accurate
azimuth, the graph should be recalculated each couple of years. Figure 3.10(f)
shows one form of this graph while another type is shown in the chapter
"Sigma Octantis azimuth determinations", Figure 3.8.
Step 2 Field
Preparations
Setting up
The following requirements
must be satisfied:-
(i)
The
instrument must be oriented with two footscrews along a N-S line so that the
instrument can be levelled in the plane of the meridian and across the plane
of the meridian. Keeping the instrument perfectly level across the
meridian is vital to the accuracy of the longitude part of the observation.
(ii) The vehicle should be
positioned so that it protects both the theodolite and the booker from the
wind, and is close enough to satisfy the next step.
(iii) The booker's table, on
which the chronometer will be placed, must be positioned within 3 paces of the
theodolite and beside the vehicle. The chronometer must be placed so that the observer
can get to it without stepping over a tripod leg.
(iv) All usual precautions in
setting up the theodolite for accurate work must be taken.
(v)
Booker
prepares his set up.
Figure 3.10(g) shows a
good lay-out.
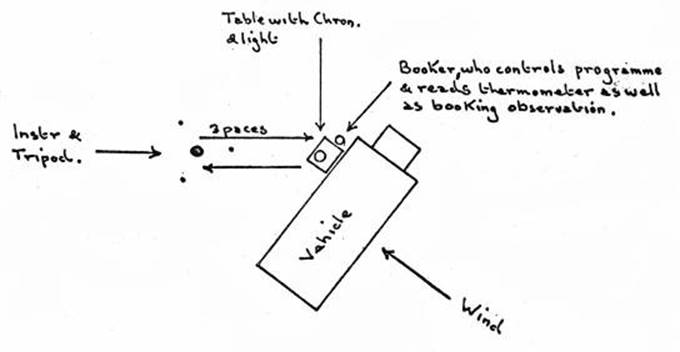
(b)
Preparations
before dark
(i)
Scale
from the map, the Latitude & Longitude to the nearest minute. Decide on the
time when Sigma Octanis should become visible and calculate the LST at this
time:‑
LST for 1900hrs WST on 1/3/71. Latitude 29°08'. Longitude 127° 16¢.
WST 19 00 00
minus zone 08 00 00
GMT (UT) 11 00 00
+ Sidereal Correction 01 49
+ Longitude in Time. (127°
16' /15) 08 29 04
+ Sid. time at 0hrs UT,
1/3/71. 10 32 35
30 03 28
-24h gives LST 24 00 00
06
03 28
From the Sigma Octantis graph calculate the ZD & Azimuth of
the star at the above LST. At 1900 hours the booker should start the pocket
watch at this LST (nearest minute.). The fact that the watch is running at mean
time rate does not matter over the short period between the time the watch is
started and the conclusion of the observation.
(ii) On the observing
programme, fill in the ZD & (360°—ZD) of each star which it is intended to
use and bracket them in "pairs" North and South; make sure a surplus
of stars are ready in case of delays. From Figure 3.10(h) the procedure is
evident.
The selection of pairs is a matter of compromise, but the
difference in the ZD's should not generally exceed 10°. The stars magnitude should generally range between 2.5 and 5.5
for easy intersection.
The observer may at times have to observe outside these limits.
However, it is generally found that stars brighter than 2.5 are too large to
intersect easily & accurately, while those smaller than 5.5 are not easy to
see. The clarity of the night will also effect this; on a very clear but
moonless night, stars in the vicinity of 6 magnitude may by intersected quite
easily, while on quite a few cloudless nights there is sufficient "murk”
in the air to make stars which would normally be quite bright, appear very
faint. Therefore these stars become the only ones suitable for observations on
this type of night.
With the ZD's of the stars, remember that the higher they are in
the sky, the less they will be influenced by refraction, thus the aim is to use
N & S stars of almost similar ZD's and as near the highest altitude the
instrument is capable of as is possible.
Obviously a N star with a ZD of 20° and a S star with a ZD of 60°
do not make a good pair as they rely too much on something which is impossible
to calculate accurately, i.e., refraction.
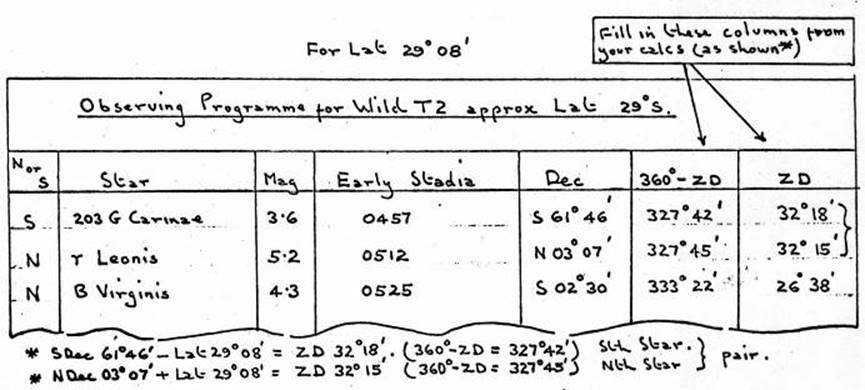
(iii) As darkness closes in, the
telescope and graticule focus are adjusted by sighting on a bright star and
"taped" with Durex to prevent movement during the observation. The
same thing applies to the micrometer telescope. The reasons for this are fully
explained later in the "Method of Observation". The theodolite should
now be levelled using the "Talcott" bubble and then laid out on an
approximate N-S line with a prismatic compass, taking into account the Mag.
Declination.
(c)
Preparations
after dark
(i)
Time
signal check
Obtain a time comparison on VNG, the Australian P.O. time signal
station at Lyndhurst, Victoria. (See Annexure C of "Specifications for
Ground Control Survey" for details of this and other time signals.) Check
the minute and second for gross error on WWVH (or WWV).
If unable to receive VNG, use WWVH (or WWV) and check minute and
second with the hourly ABC time signals.
Obtaining accurate time is entirely a matter of constant practise
in achieving a rhythmic one second beat of the finger on the stopwatch button.
Hold the stopwatch with the index finger lightly pressing on the stopwatch
button; beat with an up and down motion of the hand until the beating of the
hand and finger is in unison with the beat of the time signal. Once this synchronization
has been obtained, press the button on the stopwatch. Do not "snatch"
the button on this beat thus taking a decimal which can be widely in error.
This tendency to "snatch" and thus press the button too early is very
noticeable in the learner. A good quality stopwatch, the second divisions of
which are wide enough apart to estimate the "hundredths" is
necessary.
Step by step procedure for taking time signals.
1.
Switch
on the radio, beat watch until in unison with the second beat on the radio.
2.
Switch
off radio and go through the same procedure with the chronometer. As the
chronometer beats half-seconds make sure that synchronization is made on a full
second beat. About 10 of these comparisons must be made; the mean of all these
is recorded as the decimal of the second. Record two places of decimals.
3.
About
5 seconds before any 5 minute time signal start to beat the watch and on the
exact five minute signal press the button to start the watch.
4.
Switch
of the radio, beat until in synchronization with the chronometer, then stop the
watch on a ten second division on the chronometer. It must be remembered that
with VNG, WWVH & WWV, the 59th second of every minute is not sounded
therefore care must be taken to start beating the watch at about the 54th or
55th second so that coincidence with the time signal is obtained by the 58th
second and kept over the missing 59th second to ensure there is good
synchronization when the button is pressed on the 60th second.
5.
Write
down the second and decimal reading on the stopwatch and the chronometer. In
the stopwatch reading replace the decimal with the decimal obtained in step 2,
i.e.; if the single reading on the 5 minute is 17.8s, and the mean of the 10
readings was 0.93s the booked stopwatch reading is to be 17.93s not 17.8. Thus
if the chronometer read 19h 20m 50s and stopwatch read 17.93s at 19h 20m 00s,
the chronometer is fast:-
Chronometer reads 19h 20m 50s
Stopwatch reads
17.93s
Chronometer time (when
time signal taken) 19 20 32.07s
WST (when time signal
taken) 19 20 00
Chronometer fast 32.07s
Always take a second time check to ensure there is no mean error
of one or more seconds. If using VNG check with WWVH or WWV, or if using either
of the latter stations, check with the ABC on the hour.
(ii) Locating Sigma Octantis
using the graph
Just prior to 1900hrs, set the calculated ZD of the star on the
theodolite and commence searching East and West of the approximate meridian
until the star is identified. The ZD is the main factor in locating the star as
the Latitude is normally known fairly accurately therefore the ZD interpolated
from the graph should bring the star fairly close to the horizontal cross wire.
(iii) Final check of level
Having located the star and before laying the theodolite
accurately on the meridian, it is best to finally level the instrument as it
probably may have been moved off level while searching for the star. Level
first with the two footscrews along the meridian, then with the single
footscrew across the meridian. In future relevelling, as the level along the
meridian is not so critical it need only to be done carefully at the present
juncture, unless the theodolite is accidently knocked when complete relevelling
would be necessary. If the star was located quickly and easily, leaving the
observer confident he has not moved the level of the instrument, he may prefer
to lay on the meridian, then just touch up the level before commencing the
observation.
(iv) Laying the theodolite on
the meridian
Now calculate the ZD and Azimuth of Sigma Octantis for a
convenient LST a few minutes ahead, and intersect the star between the double
wires, at that instant. Once the star has been intersected, set the calculated
Azimuth on the horizontal circle. Turn the theodolite to 00° 00' 00" (if a
North star is to observed first) or 180° 00' 00" (if the first star is to
be a South.) Make sure the micrometer drum has been turned to 00' 00". The
theodolite is then assumed to be in the plane of the meridian and all
preparations for the observations have been completed.
The actual observation
Notes :
(a)
The
calculated values (360°- ZD) & ZD on the programme refer to the vertical
circle setting of the Wild T2 theodolite FR & FL respectively. If another
type of instrument, graduated differently, is used these values will have to be
adjusted to suit.
(b)
As the
prismatic eyepieces are only screwed in by normal thread, a drill for reversing
them must be adhered to during the observation. Otherwise they may be screwed
either right out (and fall on the ground), or right in (and cause the focus to
be altered). Therefore prior to plunging the telescope, turn the eyepieces one
half turn out when changing from FL to FR, and one half turn in when changing
from FR to FL.
(c)
Except
when actually reading the ZD of a star, the micrometer drum must always be set
at, and remain at 00' 00". If this procedure is followed the possibility
of error in setting on the meridian will be eliminated, as the theodolite has
to be laid on the meridian a minimum of 10 times during the observation, and
speed is essential, any safeguard is important. Remember, at all times, that
the horizontal circle itself is the R.O. for orienting the instrument.
Step by step procedure
1.
As the
theodolite is laid out on the meridian the first star of a pair is selected. If
the star is to the North, the instrument will be laid out at 00° 00' 00",
and if the star is to the South, it will laid out at 180° 00' 00" on FR,
in both cases.
2.
Set
the programmed 360°- ZD on the vertical circle, always estimating the minutes.
A few minutes before the programmed Early Stadia time, watch for the star to
appear. Check the identity by the star's magnitude and time of appearance. With
the vertical tangent screw bring the star to a position where it moves across
the diaphragm, just slightly above or below, the horizontal wire. See figure
3.10(a).
3.
At the
instant the star cuts the Early Stadia wire press the stopwatch button.
4.
Move
to the chronometer, beat the watch until in rhythm with the beat of the
chronometer and stop the watch on a 10 second division of the chronometer.
5.
Call
to the booker this chronometer time in the order, seconds, then minutes, then
the hour, and lastly the stopwatch reading. The assistant should repeat these
readings as he books them; also read and book the thermometer value.
6.
Return
to the theodolite, reverse the eyepieces, plunge the telescope, change to FL
and lay on the meridian at 180 00' 00" (North star) or 00° 00' 00"
(South star).
7.
Set
the programmed ZD on the vertical circle, again estimating the minutes.
Identify the star, and when it is near the centre wire intersect it on the
horizontal wire.
8.
Bring
the ends of the alidade bubble into coincidence, bring the vertical circle
graduations into coincidence with the micrometer drum, call out the ZD reading,
the assistant repeating it back as he books it. Reset the micrometer drum to
00' 00".
9.
Move
the star slightly off the horizontal wire and at the instant it intersects the
Late Stadia, press the stopwatch button.
10.
Again
move to the chronometer, beat the watch until in rhythm with the beat of the
chronometer, then stop the watch on a 10 second division of the chronometer.
11.
Again
call the readings to the assistant as in step 5, this time there is no need to
read the thermometer.
The above steps complete one star; proceed similarly with the
other star of the pair. Five good pairs are necessary, but if in doubt of the
quality of any observations, take an extra pair or two.
Relevelling between pairs of stars
Relevel, across the meridian with the single footscrew, between
each pair of North and South stars which form a complete observation. Remember
that the quality of this observation depends entirely on keeping the vertical
axis of the instrument truly vertical, particularly across the meridian and
bearing in mind that during a period of 20 or more minutes, it is exceedingly
unlikely that the instrument will remain truly level.
Time check in the middle of the programme.
Always obtain a time check somewhere near the mid-point of the
observation, say, after the third pair. This is necessary to see if the
observer is consistent in his time-keeping, or whether the chronometer has an
uneven "rate".
Time check after completion of the observing program - Drawing
time graph
The final time check should be made immediately after the last
star has been observed. Plot a graph showing the times fast or slow against the
chronometer times at which each time signal was taken. Draw a “line of best
fit" between the three plotted points to obtain a graph from which can be
read the varying amounts that the chronometer is fast or slow at the times
which each star was observed. The station number and date is noted against this
graph.
The observation with a split-hand stopwatch.
To avoid having to carry a chronometer this observation could be
done with a good quality split-hand stopwatch and using a pocket or wristwatch
for rough times.
This system would be ideal for any field party which is only
required to observe an occasional astrofix among its normal duties. Naturally,
if the party's full time task was the astrofix, a chronometer would be more
satisfactory. Full details for using the split-hand watch for Azimuth
observations are given in 3.8.10. When observing for Latitude and Longitude
these lines would be followed except that the time check procedure must be
adapted to ensure very accurate times.
As well as the full time checks prior to and after the
observation, a time check for the second and decimal (to hundredths) would need
to be taken immediately before and immediately after, each pair of stars. This
is for the decimal and second only, the other checks taking care of the minute
and hour. This check can be done quite quickly, however the delay may cause the
observer to miss some stars he would normally use; even so the full time of the
observation should not be beyond that which is acceptable.
Computation
The calculation of the Latitude and Longitude from this
observation is dealt with in 12.10.
3.11 Tacheometry or Stadia Surveying
Stadia provides a method of measuring distances and differences of
elevation by merely sighting a staff. This can be done with a level or an
orthodox theodolite providing the instrument has two horizontal crosswires,
called "Stadia Wires", at equal distances above and below the central
horizontal crosswire. These stadia wires are so arranged that the
"intercept" (the distance between the two staff readings, as read
against each stadia wire and usually called "S") is 1/100th of the
distance, instrument to staff, when the line of sight is horizontal and the
staff is truly vertical. See figure 3.11.
The level is mentioned only in passing, these notes henceforth
will deal with tacheometry where the line of sight may be inclined and where
horizon angles or true bearings will be required.
When the line of sight is inclined, the intercept is multiplied by
appropriate factors, depending on the angle of inclination; the results give
the horizontal and vertical distances from the point on the staff cut by the
central crosswire, to the axis of the theodolite.
It will thus be seen that
the bearing, distance and level of a point can be obtained in one observation.
3.11.1 Theory
As shown in figure 3.11.1, the vertical angle, a, and stadia
intercept DE (or S) have been read; required are AB (the horizontal distance)
and BC the vertical distance between the axis of the theodolite and the central
reading on the staff.
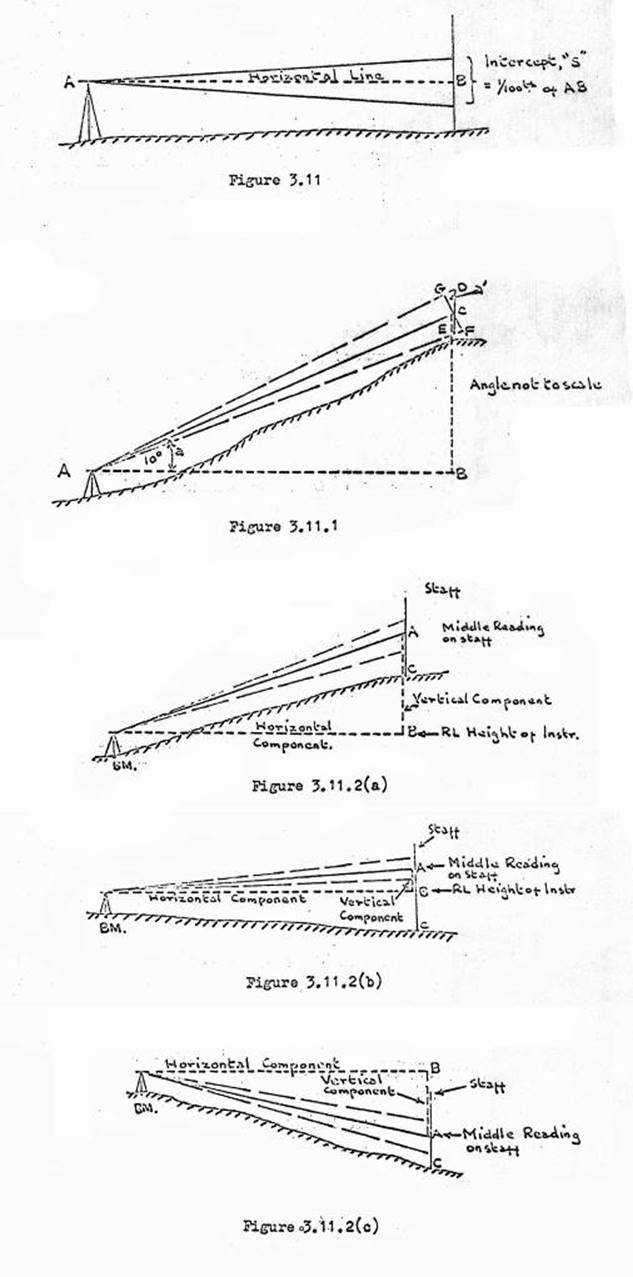
Step 1
The intercept on the staff DE, has to be turned into a distance
GF, which is a line perpendicular to the line of sight AC. The vertical angle
“a”, is equivalent to “a'”, therefore DE x cos a' = GF. In the example DE (or
S) = 4.21 and “a” = 10°, therefore 4.21 x .984 =4.146.
Step 2
With stadia 1 to 100, AC =
100 x 4.146 = 414.6.
Step 3
Solving the triangle ABC for the horizontal distance AB, 414.6 x
.9648 = 408.30.
Step 4
Solving the triangle ABC for the vertical distance BC, multiply AC
by sine 10°, that is 414.6 x .17365 = 71.995.
The above is normally
shortened to:
AB (the horizontal component,
known as H) = 100S cos2 a, and,
BC (vertical component,
known as V) = 100S sin a x cos a or
= 100S ½sin 2a.
Thus to obtain the H & V components of the sighting, the
intercept S, must be multiplied by the factors shown above. Tables are available
for these and many slide rules have special graduations so that when the
intercept on one scale is placed opposite the zero angular graduation the
horizontal component appears against the observed vertical angle in the portion
of the scale marked "H", and the vertical component appears against
the observed vertical angle in the portion of the scale marked "V".
3.1.2 Reduction
of Stadia Observations
Case 1:
Angle of Elevation with base of staff above Bench or Station Mark.
As shown in Figure 3.11.2(a) the vertical angle is an angle of Elevation, and
the base of the staff is above the BM. BM value + Height of Instrument =
Reduced Level, height of Instrument.
The vertical component (AB
in diagram) is now computed and is positive.
Add to R.L., height of Instrument to obtain R.L. of Middle Reading
on staff (A in diagram).
To obtain R.L. of point C (Ground level at base of staff),
subtract the Middle Reading on the staff from the RL of point A.
Case 2:
Angle of elevation with base of staff below Bench Mark or Station
Mark. This can occur on slightly sloping ground where it has been necessary to
elevate the line of sight to clear bushes, long grass, etc. The V.C. is
computed and is positive. Add this to. R.L. height of instrument to obtain RL
of Middle Reading on staff (A).
As in Case 1, just subtract the Middle Reading on the staff from
the RL of point A to get RL of point C. Note that in this case the R.L. so
obtained will be seen to be lower than that of the BM even though a vertical
angle of Elevation was read. See Figure 3.11.2(b).
Case 3:
Angle of Depression. The V.C. is computed and is negative.
Subtract from R.L. height of Instrument to obtain R.L. of Middle Reading (A).
To obtain the RL of point C, subtract the Middle Reading on the
staff from the RL of point A. See Figure 3.11.2(c).
Formula:-
In all cases it is R.L.
Stn B = R.L. Stn A.+ Height Instrument ± VC – MR.
In practise it is most convenient to evaluate ± VC – MR for each
point, the result being called the "difference in elevation", then
add or subtract this from the R.L. Height of instrument.
Equipment
Special theodolites and
staves are available for Tacheometry work also levels which incorporate, a
horizontal circle. However mostly an orthodox theodolite and staff will be
used; these notes, therefore will be confined to such equipment. If one
understands the theory and practise using this equipment, it is but a small
step to change to more sophisticated equipment should the occasion arise.
3.11.3 A Detail
traverse using Tacheometric Methods – Wild T2 or similar theodolite
The traverse would be
through a line of main stations, picking up detail by means of subsidiary
points along the traverse route.
Angular Work
The instrument should be checked to see that it is in good adjustment
as it is customary when laying on subsidiary points to read both horizontal and
vertical angles to the nearest minute on one face only, usually face left.
Unless a higher degree of accuracy is required, the main traverse angles, both
horizontal and vertical will be read to the nearest 10 seconds.
When the arc on Face Left has been completed, change to Face Right
on the RO and read the main traverse horizontal and vertical angle only on this
face. This helps increase the accuracy of the main traverse angles and is a
check that the circle was not disturbed during the single face readings to the
subsidiary points.
Reading the Staff
The staff must be equipped with a bubble to ensure verticality,
and a check made to see that the bubble is in adjustment before the traverse
commences.
The most simple method is to lay the bottom stadia wire on an even
foot graduation on the staff, with the centre wire somewhere in the vicinity of
5 to 6 feet; i.e., approximately the same height as that of the theodolite.
Staff readings along the main traverse line are read twice, i.e.
forward and backward, the distances and heights must be calculated in the field
to check for gross error. Distances should agree within 1 foot and difference
heights within 0.10 ft.
3.11.4 Field
Book
There are various forms of field notes, That shown in Figure 3.11
is recommended for completeness and for clarity.
Column 1. The number (or name) of the station, RL station
mark, height of Instrument.
Column 2. Sketch of the traverse legs and details of
subsidiary points oriented on magnetic bearing.
Column 3. The station observed.
Column 4. The Horizontal angle observed.
Column 5. The Vertical angle observed; indicated positive or
negative.
Column 6. The three readings on the staff.
Column 7. The "intercept", S.
Column 8. The calculated horizontal distance.
Column 9. The calculated vertical component, indicated
positive or negative.
Column 10. The difference in elevation, indicated positive or
negative (obtained from the algebraic sum of Mean Reading on staff & V.C.).
Column 11. The Reduced Level of the height of instrument; data
from Col 1.
Column 12. The Reduced Level of the distant traverse station or
subsidiary point; obtained from the algebraic sum of columns 10 and 11.
Column 13. Space for any necessary notes.
3.11.5 Errors
caused by changing focus of the theodolite telescope
For internal focusing telescopes, which are the only type likely
to be encountered, the factor D = 100 S, changes slightly with changing focus
and varies slightly from instrument to instrument.
These variations are negligible except for very accurate
measurements. For such determinations, it will be necessary to plot a
correction curve for the instrument being used. The corrections are obtained by
measuring exact stadia intercepts at various accurately measured distances; the
following are recommended: 25, 50, 100, 200, 400, 800 and 1600 feet.
3.11.6 Accuracy
Horizontal Distances
An accuracy of about 1 in 1,000 would be about the best expected.
The serious sources of error are in the measurement of the intercept and the
verticality of the staff.
Errors arising from the measurement of the vertical angle and, the
multiplying constants are negligible.
Heights
On a sight of 1,000ft, with a vertical angle of 6°, and allowing
for a horizontal distance accuracy of 1 in 1,000, the error in the difference
height could be about plus or minus 0.10ft; however with a sight of 500ft and a
vertical angle of 1°, the error could be only about plus or minus 0.01ft. Therefore
unless size of vertical angle and length of sight are taken into account, no
figure for accuracy can be given. The following can be used as a guide :
For average length lines,
(up to about 700ft) and with average vertical angles (up to about 5°) the best
accuracy of difference heights between points would be about plus or minus
0.05ft.
3.11.7 Curvature
& Refraction
The influence of curvature and refraction on heighting by
Tacheometric means commences to show once sights reach 700 feet in length,
where it is still only about +0.01ft. However, as it increases with the square
of the distance, it becomes about +0.57ft at one mile (5280ft).
From these figures it can be seen that not a great number of
sights will be affected. If the vertical angles on sights above 700ft are
observed reciprocally, and the mean of such angles used curvature and
refraction will be eliminated. This is the best method to adopt.
For further notes on curvature and refraction, including the
calculations necessary to obtain the curvature and refraction for any line
where angles have been observed from one end, only, see Section 12.4.
3.12 Almucantar observation for Longitude with
Wild T3 Theodolite and stopwatch
For this observation, the instrument must be
fitted with a graticule having 5 horizontal intersections on the vertical wire,
each 5 minutes of arc apart (i.e. two above and two below the central
horizontal cross-hair).
Also the
alidade bubble must be graduated at approximately 2 mm intervals.
Graticule Alidade
bubble graduations, Wild T3 on F.L.
Figure 3.12 (a)
Stopwatch
This must be of
the split-hand type and be of good quality with a large dial, clear figures and
graduated to 1/10 second; estimate to 1/100 sec.
Pocketwatches
An accurate Pocket or sweephand wrist watch
is necessary. This watch must have the capability of the second hand
"marking time" when the winding button is held out so that second and
minute hands can be synchronised.
In addition
another watch, or even an alarm or travelling clock is necessary as a "Prediction"
watch.
Prediction
Sheets
See Technical
Report 4 for details of the preparation of Data Sheets for the electronic
computation of Prediction Sheets for this observation with the Wild T3
theodolite.
The predictions are prepared for the
approximate date that observations are to take place; in the Longitude
programme each star is listed by Number, Magnitude, True bearing (nearest
minute) and Time. The time is the standard time for the relevant time zone, i.e.
in Australia EST, CST or WST as the case may be. If observations are not done
on the exact date programmed, an allowance of 3.94 minutes (3 min 56 secs) per
day must be made. That is, stars will be at the sane elevation 3.94 minutes
earlier each day. This can be allowed for by pencilling in the correct time for
the observing date or by setting a separate "prediction" watch to
agree with the programme. If observations are later than the programmed date,
the stars will be early therefore the watch must be set fast. See Figure 3.12
(b) for a prediction sheet, Wild T3.
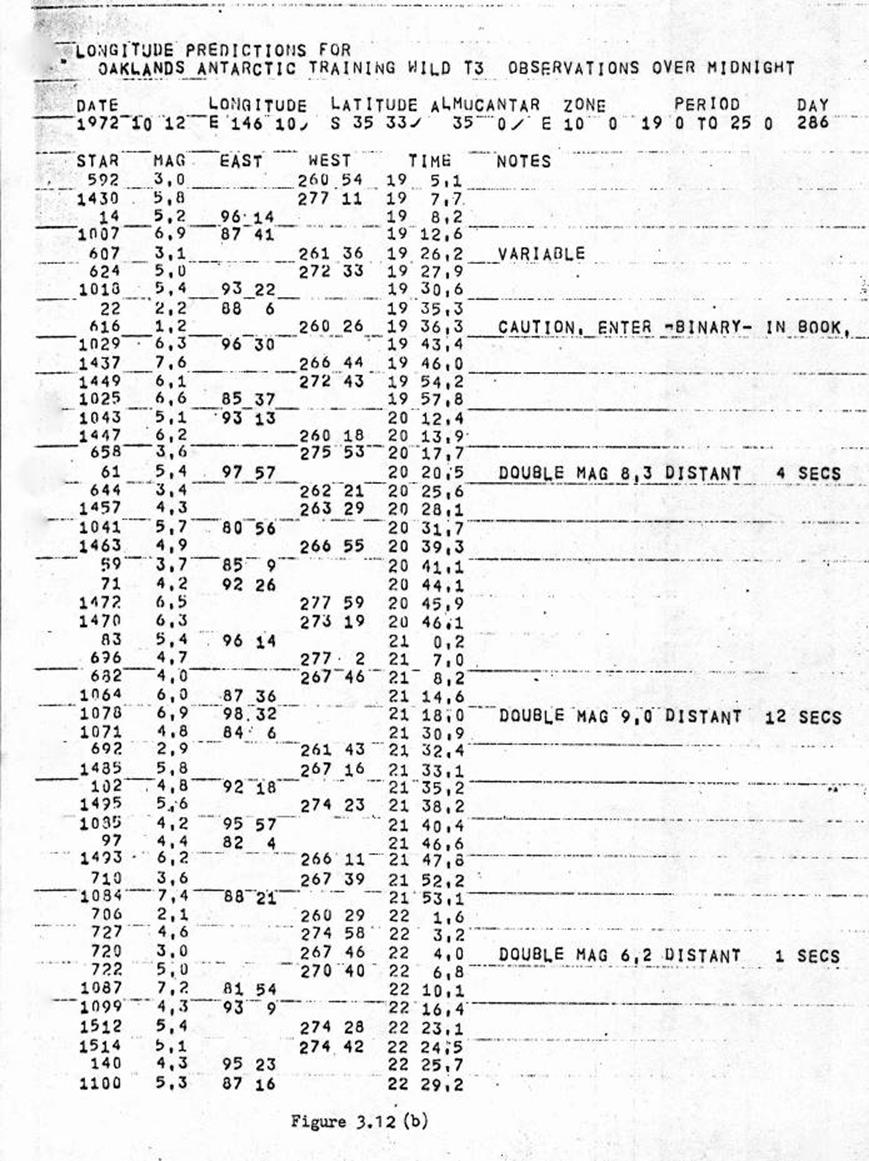
Radio
A good quality transistor radio with a short
wave band capable of receiving WWVH or VNG (Lyndhurst, Victoria) is required.
It should be noted that with the recent introduction of "atomic" time
there will now be a correction, varying with the date, to be applied.
Number of Pairs
As distinct from the Latitude observation
there is nothing to gain by selecting pairs in advance. Any East star can be
paired with any West star, providing they are observed within twenty minutes of
time. The aim should be 16 pairs, 8 on each of 2 nights; the minimum is 12
pairs with not less than 6 pairs on each of 2 nights.
Time Signals :
setting the main watch and stopwatch
About 30 minutes before observations are to
commence, but not on an exact hour or half hour, the main watch should be set
by radio time signal, about 10 seconds fast. Take care to synchronise the
minute hand and second hand or in other words don't have the second hand 10
seconds fast and the minute hand in a position which indicates about 30 seconds
fast (or slow).
On the next even hour or half hour on this
watch, the starting button on the stopwatch is pressed so that the stopwatch is
started in syncronisation with the main watch. Lock the starting button of the
stopwatch with a clip made from a "glider" clip. This will prevent
the whole observation being wasted if the wrong button is pressed during the
observation.
Beating the
watch
The accuracy of the Longitude observation
using a stopwatch is completely bound up in the observer's ability to
rhythmically beat the stopwatch in unison with the "beep" of the
radio time signal obtaining such consistency that the mean of his beatings will
be close to 0.05 seconds plus or minus personal error. (See personal equation).
Much practice
is needed and care must be taken to avoid making whole second or whole minute
errors while concentrating on obtaining the accurate decimal of a second.
Beat the finger on the stopwatch button a
number of times until this slight sound is synchronised with the beat of the
radio time signal. Once this is achieved press the button on one of the beats.
Do not "snatch" on this beat; learners tend to do just this after
having got into a good rhythm. Thus having lost this rhythm on the final beat
their result could be 0.1 second or more in error. The mean of 5 series of
signals is taken, see Figure 3.12 (c) for an example of the time signal page of
the field book.
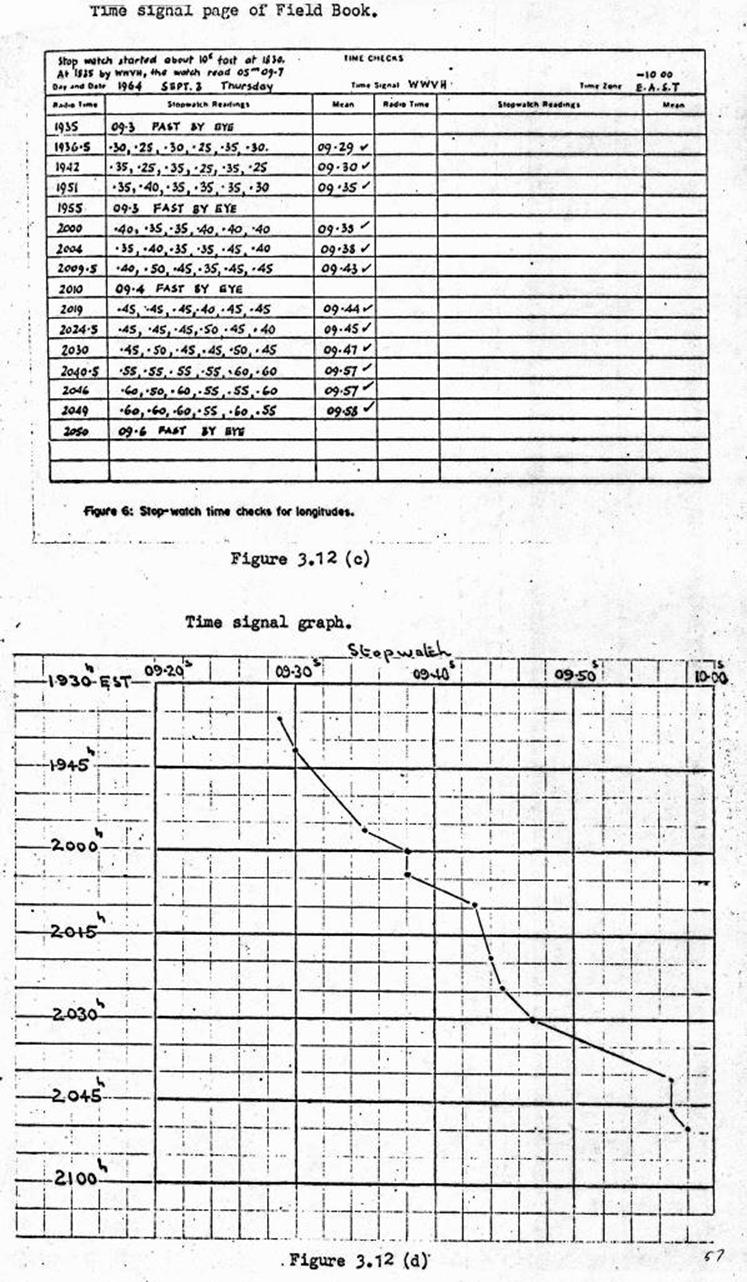
When to take
time signals
In the longitude observation using a
stopwatch, a fresh time signal is required just before every star; now and
again it is permissible to omit one of these signals when stars follow in close
succession, however never book more than two stars without taking time signals.
If there is a long interval of about 10 or more minutes between stars, a time
signal should be taken immediately after the star has been booked and a fresh
time signal just prior to the next star.
The
"rate" of the stopwatch
This is most likely to be even if the tension
on the main spring is kept about the same; therefore make a drill of keeping
the watch fully wound – wind it just before taking each time signal. At the
conclusion of the observation, graph the time signals at a scale which can
easily be read to 0.01 second. Join each point with a straight line. If the
correct procedure has been maintained the graph will be reasonably smooth; a
"jagged" graph can indicate any of the following and gives warning
that some action is required :
i.
More practice, or care in beating the stopwatch.
ii.
Watch not being kept fully wound, thus tension on the main spring
is inconsistent and "rate" suffers.
iii.
Watch in poor condition, needs overhaul.
The graph will also show at a glance if too
few time signals have been taken, or if they have been inconsistently taken,
i.e., a few at close intervals but long gaps between others. Too few time signals
combined with a jagged graph would mean the observation must be considered
unreliable. See Figure 3.12 (d) for a time signal graph.
It is a good plan, for safety, to have the
stopwatch on a loop of string around the neck. Do not let it swing free when
not in use but keep in a coat or shirt pocket. Although a stopwatch is robust
it must be treated as a delicate instrument where an even "rate"
suitable for accurate Longitude observations is required.
Theodolite
setup
An observing screen should be used. The
tripod should be set on three firmly driven pegs, wooden for preference. Pegs
to be driven on an angle in conformity with the slope of the tripod leg.
The tripod should be set so that the
theodolite will have two footscrews along the line of the meridian; this can be
done accurately enough with a prismatic compass. An essential of this
observation is that the alidade bubble must be altered slightly after each
timing of the star, by moving the ex-meridian footscrew.
Level the instrument carefully, firstly with
the plate bubble then finally with the alidade bubble. The instrument will be
used on Face Left to agree with the prediction programme. Set the horizontal
circle on the meridian by laying on Sigma Octantis at its calculated true
bearing or by turning a true bearing from a distant survey control point, if
available.
The Almucantar prediction will be for either
30° or 35° altitude, with 30° being best for the T3. This altitude plus
refraction must be set on the vertical circle. With the older model Wild T3
theodolites which have vertical circles that read half the angle, the setting
will approximately be 105° 00' 25" or 107° 30' 20" depending whether
30° or 35° predictions are to be used. Clamp the vertical circle firmly,
throughout the observations.
The following
three points should be kept in mind during this observation.
(i) The essence of
the observation is timing a star across a series of 5 hairs, and each time
reading the alidade bubble.
(ii) Not one angle
is read while laid on each star.
(iii) The only
control screws moved are the ex-meridian footscrew to vary the bubble and the
horizontal slow motion screw to keep the star close to the vertical wire as it
cuts the five horizontal wires.
The observation
Look for a
trial star of a fair magnitude to test the predictions, the time set on the
prediction watch, the azimuth and altitude setting.
The eyepiece prisms will be required on the
theodolite. Stars come into view about two minutes before the predicted time
assuming the correct data has been supplied for the electronic computing of the
programme. If the star is not sighted fairly close to the predicted time make
the following checks in the order listed :
(i) Check that the
prediction watch has been set correctly, i.e., 3.94 minutes (3m 56s) per day
adjustment may have been applied the wrong way or not applied at all.
(ii) Check that the
theodolite has been laid accurately in azimuth.
(iii) Check that the
theodolite has been laid on the same Altitude as shown on top of the Almucantar
prediction sheet.
If all the above are correct it would appear
that an error has been made in the data supplied for the prediction. If this is
a gross error it may possibly be rectified if an FK4 star catalogue is
available, i.e. locate a well known star which is predicted, observe to the
nearest minute its azimuth at the moment it cuts the almucantar circle and
record the time to the nearest minute. There is every possibility that if the
predicted stars are all corrected by the same difference in bearing and time as
indicated by the observation on the known star, the prediction sheet will then
be accurate and the observation can go ahead.
If this does
not solve the problem it will be necessary to request new prediction sheets.
Assuming that
the trial star appeared as predicted, get ready to proceed with the observation
:
1) Check and
adjust level if necessary.
2) Check that the
vertical circle has been set correctly, get booker to record setting on top of
field book page.
3) Decide on first
star, lay on predicted bearing.
4) Take time
signal, record results.
5) Watch for star
to come into view; verify its identity by estimating the magnitude, set alidade
bubble with the ex-meridian footscrew so that the ends are just a little apart
(say between 0.1 & 0.4 of a graduation).
6) With the
horizontal slow motion screw the star is positioned so that it will cut the
first horizontal wire close to the vertical wire, call to the booker "Star
coming in", so that he can concentrate on reading the main watch to the
nearest second.
In Australian
latitudes the interval between the hairs is about 22 seconds of time; during
this interval the observer has to complete the following 4 steps :
1. Call
"Up", simultaneously pressing the stop watch button.
2. Read the
stopwatch, and when the booker has called back the reading, re-start the second
hand.
3. Read the
alidade, alter it by touching the ex-meridian footscrew, balancing the error in
so doing.
4. Adjust the horizontal
slow motion screw to bring the star close to the vertical wire ready for timing
it across the next hair.
Proceed with the second, third, fourth and
fifth hairs in the same manner. Swing to the azimuth of the next star, making
sure that the horizontal slow motion screw is about central in its run.
Take a time
signal, return to the theodolite and observe again as outlined for the previous
star.
Two points
which need further emphasis are :
1. Alidade bubble
readings.
The bubble is graduated as shown in Figure
3.12 (a) each division is about 5" to 6" of arc. No attempt is made
to bring the ends into exact co-incidence, the readings are estimated to the
nearest tenth of a division, and if the reading on the first hair is +0.3, the
bubble is altered with the ex-meridian footscrew to read -0.3 for the second
hair and so on. If the plus and minus readings over the five hairs are
deliberately set so as to almost balance out, any error in the calibrating of
the bubble automatically cancels out.
In becoming
familiar with his instrument the observer should do two things, i.e. :
1) Move the bubble
with the alidade screw and assure himself that the vertical angle is indeed
plus or minus of the actual reading when in the positions shown in Figure 3.12
(a).
2) Calibrate the
alidade bubble to ascertain the value of the graduations; proceed as follows :
(i)
On Face Left lay on some target that can be finely bisected. This
is only necessary to prove that the vertical axis is not moved during the
course of the calibration.
(ii)
To calibrate, move the bubble with the alidade adjusting screw to
one end of its run; let it settle.
(iii)
Check that the telescope has not been moved off target, read
vertical circle and bubble.
(iv)
Move bubble about one sixth of its run, let it settle and again take
vertical circle and bubble readings.
(v)
Repeat until bubble is at the other end of its run. Readings can
more advantageously be made more frequently towards the ends of the bubble’s
run and less frequently in the middle.
(vi)
Check again that the telescope is still on target, and take
another series of readings back up the bubble’s run, to the starting point.
(vii)
Make a final check that the telescope is still on target.
(viii)
Calculation of the value of a division is best done graphically.
Firstly convert the T3 readings to seconds of arc remembering that the older
model reads only half the angle on the vertical circle and that both models
also have the micrometer drum graduated at 60" for a two minute run. Plot
a graph of seconds of altitude against bubble divisions. Draw a straight line
through the points using a transparent ruler to judge the mean position. Avoid
simply joining the two end points, which in effect discards all the other
readings. Determine the slope of the line in seconds per division. With some instruments
it may be found that separate parallel lines are obtained on the graph, one
when the altitude is increasing and the other when it is decreasing - this is
due to backlash. When this defect is found, the cure is always to make the last
adjustment to the alidade bubble in a clockwise direction, regardless of
whether one needs to move the bubble up or down. Few observers do this, and
with a new instrument it is not essential, however it is clearly a good habit
to get into.
2. Missed
Stopwatch readings on any hair
One missed hair
does not invalidate that star. If a hair is missed :
(i) In finalizing
the field book, the observations for the symmetrical hair must be cancelled. If
the first or last hair is missed, use the centre three, if the second or
fourth, use hairs one, three and five, if the centre is missed use the other
four.
(ii) Observations
for the same hairs must be struck out for the other star in the pair.
(iii) Count a pair of
stars with missing hairs as half a pair only: if the programme requires eight
pairs, they could consist of seven perfect pairs, plus two pairs with missing
hairs.
Check the
Vertical Setting
After every
four pairs, and at the end of the observations, check the vertical circle
setting and record it on the top of the page of the field book, thus :
"Vertical
circle checked and found to read………………..”
If the setting has changed more than 2",
record this and reset the circle to the original value before continuing with
the observation. If the error is found while a pair is incomplete, complete
that pair before re-setting the circle. Remember that if during the observation
of a pair, the vertical circle slow motion screw or the alidade adjusting screw
are moved the observation on that pair is ruined.
Booking
As in most astronomical observations, apart
from "position lines", the observer relies heavily on his booker. The
booker should have a table and chair if possible. If this cannot be managed he
must have a large booking board and a rolled up swag to sit on, also a good
light which can be shielded so as not to hinder the observer. Paper clips or
rubber bands to prevent the field book pages and prediction sheets from
becoming unmanageable, are a necessity.
If the booker is experienced, in many ways he
will run the observation by selecting the stars, advising the observer when and
on which bearing to look for the next star, also advising the time available in
which to take a time signal.
The observer will advise "Star
sighted" and give estimated magnitude. The, booker will check this with
the magnitude of the predicted star and call "Seems OK" or
"Large difference in magnitude" as the case may be. Observations on
many wrong stars have been prevented by this simple check.
If the
magnitude indicated that the correct star was in view the booker carries out
the following sequence as the observation on that star progresses :
(i) Writes the
page, star number and aspect in the field book.
(ii) Concentrates on
the main watch and records in the appropriate "box" the time to the
nearest second at the observers call of "Up".
(iii) Enters
stopwatch time and bubble reading in the appropriate "box" beneath
the main watch time calls these back to the observer.
The above
sequence is completed for each of the five hairs; if a hair is missed write
that word in the appropriate "box".
On completion of that star the booker calls
the next bearing and time available, and so on through the observation, also
advises the observer to check the vertical circle after each 4 pairs have been
completed. During this observation the booker has no reductions to do; however
he should keep alert for gross errors in the stopwatch readings, and mean the 5
bubble readings to ensure they are indeed being "balanced" as
mentioned previously and should advise the observer if care is not being taken
along these lines.
"Pairs" are numbered as they are
completed, not in advance, too often some type of delay prevents a planned
observation taking place. With a very experienced booker the best plan is to
have all the East stars on the Left hand page and the corresponding West stars
on the Right hand page, thus the pairs are on the same line across the double
page. However it has been found that a less experienced booker soon enters an
East star among the West or vice versa. For this reason it is probably better
to enter all stars in chronological order down the page. Always save the
prediction sheets and return them with their respective field books. See Figure
3.12 (e), for a field book page.
Observers
Personal Equation
This is determined by observing stopwatch
longitudes at a station whose longitude has already been determined
impersonally. The minimum of observations to give a single reliable calibration
would be eight pairs on each of three, or preferably four nights.
As time is not always available for such a
programme a good practical solution is to make the normal observation of eight
pairs on two nights at the calibration station before the first and after the
last of a group of up to 5 new stopwatch longitude stations.
Compilation of
Longitude data sheets
The preparation of these for the T3
observation is described in Technical Report No.4. Also there are now
available, from the Division's Canberra Office, field books in the form of data
sheets for many types of field observation. They incorporate carbon-impregnated
paper for the original page, thus the data sheet is available without rewriting
and a duplicate copy is left in the field book as a record of the original
observations.
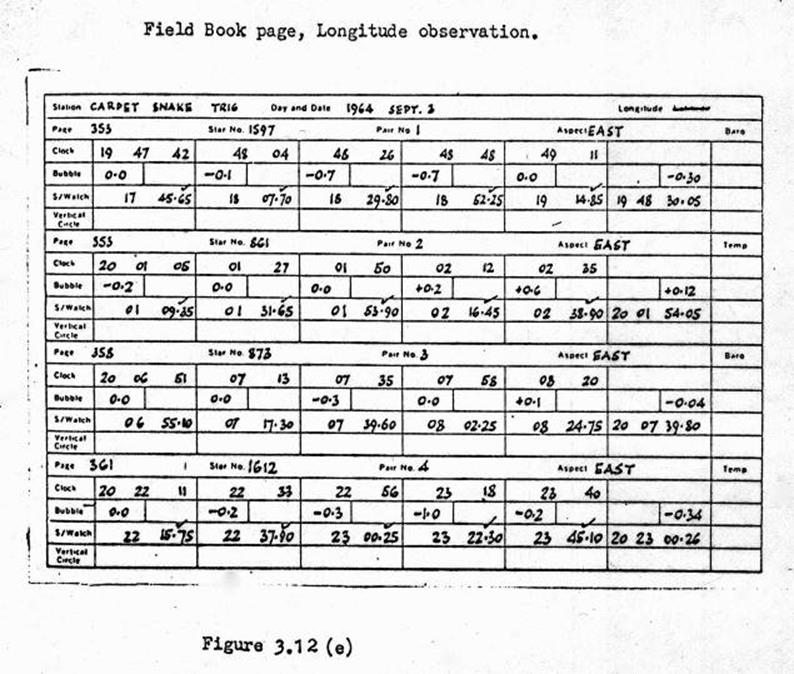
3.13 Latitude observations with the Wild T3 Theodolite – Meridian or
Circum-Meridian Altitudes
General
This is the companion
observation to the Almucantar Longitude observation. Data sheets for
predictions are prepared at the same time as those for Longitude - See
Technical Report No. 4 for notes appertaining to the Wild T3.
With that
instrument stars within the altitude band 30° to 60° are suitable, and all
readings are taken on Face Left.
Much of the data in the
notes on the Almucantar observation of Longitude, with the Wild T3 and
stopwatchl apply to this observation and will not be repeated, but the main
differences in emphasis will be pointed out. These are :
(a) In the
Longitude observation, very accurate time and alidade bubble readings are the
main factors and no angles are read. In the Latitude observation, almost the
reverse applies, very accurate vertical angles combined with alidade bubble
readings are the basis of the observation. Time signals are taken in the same
manner as described for the Longitude observation but only at the commencement,
mid-way and the conclusion of the observation. If cloud causes long delays time
signals should then be taken each half hour during this delay. Time signals are
graphed at the conclusion of the observation.
(b) Alidade bubble
movements in the Longitude observation are made with the ex-meridian footscrew.
In the Latitude Observation normal usage of the instrument applies therefore
the alidade bubble is moved with the alidade adjusting screw.
Selecting
"Pairs"
In contrast to the Longitude observation it
is advisable to select pairs in advance of the observation. They are paired
North and South within 4° of altitude and 20 minutes of time, trying to find a
partner among the many North stars for each of the rarer South stars.
Observations on
a single night are acceptable but 8 pairs on each of two nights should be the
aim, 12 pairs being the minimum.
Number of Shots
per Star
With the wild T3 which has a maximum altitude
of about 60°, six shots are required. The maximum time allowed in which to
complete these is six minutes, i.e. three minutes each side of upper transit.
Note that it is better to obtain a few shots to many stars, than many shots to
few stars.
The observation
The setup,
laying out of the theodolite on the meridian, time signals etc are as for the
Longitude observation except for the slight differences mentioned previously.
If the setting of the horizontal circle and
the prediction watch have not already been tested on the Longitude programme,
follow the same procedure by checking the transit time and altitude of the
first reasonably bright star.
Assuming all is
correct proceed as follows :
(i) Set the
predicted reading on the vertical circle and swing on to the meridian, North or
South as the case may be.
(ii) Find the star,
call "Star seen" and verify the magnitude with the booker.
(iii) Estimate how
long it will take to get 3 shots before upper transit, move the theodolite
horizontally so that the first cut can be taken on the horizontal wire but
close to the vertical wire. Set alidade bubble with the alidade bubble
adjusting screw just slightly off level, and call "star coming in" to
warn booker.
(iv) Call
"Up", simultaneously pressing the stopwatch button.
(v) Read stopwatch,
bubble and vertical circle. The booker will read these back as they are given.
Re-start stopwatch second hand once this has been read back.
(vi) Move alidade
bubble fractionally with alidade adjusting screw.
(vii) Again move theodolite
horizontally so that the second shot will also be taken close to the vertical
wire. Repeat the above sequence until the six shots are taken, a shot every 30
seconds being the aim.
As in the Longitude observation the plus and
minus bubble readings should purposely be made to balance out; they should
range somewhere between +0.5 and -0.5 over the 6 shots on each star. This
system helps to nullify any error in the graduation of the bubble, and also a
"sticking" bubble, by keeping the mean altitude almost independent of
bubble readings.
The degrees and minutes of altitude need only
be read on the first and last shots. After the last shot immediately re-set the
horizontal and vertical slow motion screws to the centre of their runs, then
set the instrument on the meridian and at the predicted altitude of the next
star.
Booking
Most of the
general notes regarding booking of the Longitude observation will again apply
and the same field book is used.
It is best to book the North stars on the
Left hand page and the South stars on the Righthand page, however once again if
an inexperienced booker is likely to get them mixed it is better to book them
in chronological order down the page. The sequence of operations for the booker
is :
(i) Advise the
observer the time available, the altitude and aspect of the star.
(ii) Observer will
give estimated magnitude; booker will check this with the actual magnitude
listed and advise observer if there appears doubt.
(iii) On the
observers call "Star coming in", concentrate on the main watch and
record time to the nearest second on the call, "Up".
(iv) Read back in
turn, stopwatch, bubble and vertical circle readings.
Proceed with steps (iii) and (iv) again until
the six shots on that star are completed; enter page, star number, pair number
and aspect in the field book. See Figure 3.13 (a) for an example of a field
book page.
During gaps in the programme the booker
should advise the observer when to look for the next star, when to take time
signals etc. He is also responsible for recording temperatures and pressures
for Refraction. The thermometer must be hung where it indicates the true
external air temperature, the thermometer being read to the nearest degree
Celsius and once per pair of stars, unless it is falling rapidly when it should
be read once per star.
The pressure
should be taken every half hour. If a battery of altimeters is used, readings
will later have to be converted to millibars.
Compilation of
Latitude data sheets
See notes in
Longitude observation.
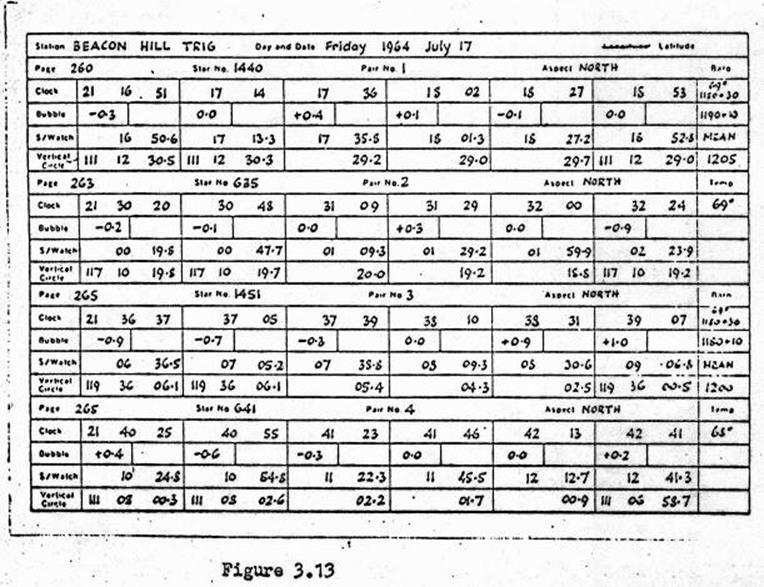
4 Tellurometer MRA-2
4.0.1 Setting up
Set the tripod firmly in the ground using foot pressure on the
metal shoes. Level the tripod head by adjusting the tripod legs. In very windy
conditions it is wise to take precautions to prevent the instrument from being
blown over. The tripod should be securely anchored to the ground by retaining
stays tied to the top of the tripod legs. Alternatively rocks can be stacked
around the tripod shoes.
Procedure :
(a)
Remove
from the haversack and place the instrument on the tripod head. Steady it with
one hand and secure it loosely with the tripod securing screw. Move the
instrument on the ball joint on the head until the point of the plumbob is
exactly over the station mark. Tighten the screw until the instrument can just
be rotated on the tripod.
(b)
Remove
the operating-panel cover by unscrewing the wing-headed screw. Also remove the
cover of the antenna boss on the side of the instrument by operating the lever
and pulling of the cover off.
(c)
In
order to remove the reflecting dish and the dipole which are securely held
inside the operating panel-cover turn the knurled head of the retaining device
anticlockwise until the spring-loaded and plunger arm coincides with the long
slot. Turn the knurled head up to the limit of the slot then anticlockwise as
far as it will go. Disengage the dipole from its spring clip and withdraw the
reflecting dish. Protect the dipole while the reflecting dish is being fixed
into its position.
(d)
Secure
the reflecting dish into its operating position on the instrument by inserting
the pegs (on rear of the reflector) into the holes provided in the antenna hub
releasing the spring-loaded locking lever.
(e)
Plug
the dipole securely into the sockets.
(f)
Using
the cable provider connect the instrument to the battery watch carefully that
the polarity is correct. The cycle lamp should light up immediately.
(g)
Allow
10 minutes for the oven to warm up. The oven should cycle four times before
measurements are commenced.
(h)
The
instrument is now ready to use.
4.1 Description of Tellurometer MRA-2
4.1.1 General
The following is a description of the various assemblies, and
controls, switches, meters etc on the operating panel. It also furnishes the
operator with sufficient information for the proper operation of the
instrument.
The major component
assemblies of the instrument are :
(a)
the
antenna assembly comprising the reflecting dish and dipole.
(b)
the instrument
case and covers.
(c)
the
operating panel.
(d)
the
transistorised power supply.
4.1.3
Controls, switches, meters
Brilliance
This control is used to
adjust the brilliance of the trace on the cathode ray tube (CRT). The FOCUS
control should be used in conjunction with the brilliance control.
Focus
This control is used to
adjust the sharpness of the trace on the CRT.
X Shift
This control moves the
spot in a horizontal direction across the face of the CRT. It should be
adjusted until the spot is a centred within the graticule.
Y Shift
This control moves the spot in a vertical direction across the
face of the CRT. It should be adjusted until the spot is centred within the
graticule.
Shape
This control is used when the instrument is operating as a MASTER;
it adjusts the shape of the display on the face of the CRT. The control should
be adjusted until the major axis of the ellipse corresponds with the X axis.
Y Amplitude
This control is used when instrument is operated as a MASTER, in
order to adjust the amplitude of the ellipse in the vertical direction until it
becomes a circle. After the axes of the ellipse have been bought into
coincidence with the X and Y axes of the CRT and the Circle Amplitude control
has been used to just the major diameter of the ellipse to be equal to the
diameter of the graticule circle, the Y Amplitude control is used to adjust the
miner diameter to be the same as the diameter of the graticule circle.
Circle Amplitude
This control is used when instrument is operated as a MASTER, to
adjust the circular presentation on the CRT by increasing or decreasing its
diameter, until a satisfactory circular trace is obtained.
Check pulse
This switch is used in the Master position to convert the circular
presentation on the CRT to a display on the master from the remote station thus
the master operator can ensure sufficient pulse is being received from the
remote station and if not instruct the remote operator to increase the pulse
amplitude.
Graticule lamp
This is used to set the level of illumination necessary on the
graticule.
Cavity Tune
This is situated at the top left of the panel and comprises a knob
with an integral turns counting dial.
The control is used to adjust the resonance frequency of the
cavity by altering the position of double plunger inside the cavity. As the
knob is turned clockwise the plunger is moved further into the cavity thus
increasing the resonance frequency. When the tuning adjustment is made it is
usually necessary to retune the klystron reflector using the reflector tuning
control. Tuning of klystron cavity should be undertaken only when the
instrument is in the SPEAK position otherwise it is possible to tune into a
side band. There are many cavities spaced about 10mc/s apart. The cavity should
always be tuned for maximum AVC reading. The Master instrument should always
tune to the Remote and should always be 33mc/s lower in frequency. The knob is
graduated from 0 to 10 and has a fine scale on which 100 divisions
corresponding to one division on the coarse scale.
Speak/Measure switch
This key switch is used to select the “Speak” or “Measure”
functions of the instrument. It is also used as a means of signalling when the
Master operated wishes the Remote operator to change patterns. When this switch
is momentarily flicked from “Measure” to “Speak” the 1kc/s monitoring signals
in the remote earphones and on the remote cathode ray disappear, and this is
customarily used as an indication to the Remote operator to change to the next
pattern.
The Pattern Selector switch
This is located below the Speak/Measure switch. It is used to
select first the function MASTER or REMOTE, then the pattern (A, B, C or D),
and at the Remote station that type of 1kc/s signal (Forward or Reverse) on the
A+ and A- patterns. It has twelve positions as follows :
Master Remote
A A+R,
A-R, A-F or A+F
B B
C C
D D
If the selector switches are not synchronised the monitoring
signal in earphones and a presentation on the screens of both the Master and
Remote stations will disappear.
Pulse amplitude
This is used when instrument is operated as a REMOTE. Adjusting as
required by the Master operator in order to increase or decrease the pulse
level until the optimum size of the break is obtained on the circular trace.
Reflector tune
This is situated at the bottom left of the panel and is adjusted
for peak crystal current which is in effect a measure of the output power from
the klystron.
Input supply socket
This is located at the bottom centre of the panel and it should be
connected with the cable supplied to the battery.
Power switches
The LT (low tension) On/Off switch is used for switching power to
the tube heaters, the klystron heater, and the transistorised power supply. The
HT (high tension) On/Off switch, which must be operated not less than half a
minute after the LT switch, is used to switching to be +250V and -230V outputs
from the power supply.
Fuses
Two fuses are incorporated in the units :
The LT fuse is rated at 10A;
the HT fuse is in the HT line and is rated at 100mA.
Crystal current meter
This is situated to the left of the LT fuse and indicates the
current flowing through the crystal mixer in the dipole assembly. The current
is adjusted by the Reflector Tune control.
Switched meter
This is situated to the right of the HT fuse, and used in
conjunction with the METER selector switch, to monitor the instrument. When the
switch is set to REG the meter indications should be between 20 and 80μA.
A reading below 20μA indicates a flat battery or faulty power supply. When
the switch is in the MOD position the meter should indicate 40μA for the
A, B and C patterns and 36μA for the D pattern. When the switch is in the
AVC position the meter reading for the short range operations should be about
60μA and for long-range operations about 20μA.
Meter selection switch
This is situated below the HT fuse and is used in conjunction with
the Switched Meter above. It has three working positions :
REG : where current through the regulator tubes is measured;
MOD : where the level of the output from the oscillator i.e. the
level of modulation is measured;
AVC : where the strength of receiving signals are indicated on the
meter.
Panel lamp control
This is situated on the left of the Cavity Tune and it sets the
level of the internal illumination of the panel.
Oven cycle lamp
This is situated top centre of the panel. It indicates whether
power is being supplied to the crystal oven and lights up when instrument is
connected to a battery.
Headset socket
This socket marked PHONE is situated the bottom right of the
panel. The headset is plugged into the socket for speech communication.
4.1.4 Pre-operational
checking
(a)
Switch
on the LT switch. After 30 seconds switch on the HT switch.
(b)
Set
the Meter Selector switch to read REG. A reading of at least 20μA on the
Switched Meter indicates a flat battery or faulty power supply.
(c)
Set
the Speak/Measure switch to Measure and the Meter Selector switch to MOD.
Switch the Pattern Selector in turn to A, B, C and D, Master and Remote. In
positions A, B and C the reading on the Switched Meter should be 40μA; in
position D it should be 36μA.
(d)
Rotate
the Reflector Tune control for maximum reading on the Crystal Current Meter. A
reading of reasonable amplitude signifies that the Klystron is oscillating and
the crystal mixer is functioning.
(e)
Set
the Speak/Measure switch to Speak and check the thermal noise in earphones.
(f)
Observe
whether there is a spot on the cathode ray tube and check the operation of the
X Shift, Y Shift, Focus and Brilliance controls.
(g)
Check
whether the graticule lamp control varies the level of illumination on the
graticule and also whether the panel-lighting control operates satisfactorily.
4.2 Operation under usual conditions
The following general
pattern should be followed for all measurements :
(a)
Setup
the instruments at 2 stations
and tune them in.
(b)
With
the Remote unit, on its initial CAVITY TUNE setting (say ONE) and the Master tuned below
it take a complete
set of "coarse” readings (A+, A-, B, C, and D). Repeat on cavities THREE
and TEN.
(c)
Take
initial readings of atmospheric pressure and wet and dry bulb temperatures
(d)
On
CAVITY TUNE setting TEN, take a set of “fine" readings (A+F, A-F, A-R,
A+R). Repeat in half cavity
settings down to cavity THREE.
(e)
Take a
final set of atmospherics. This is also the first set for Remote.
(f)
The
Remote now becomes the Master, "fine" readings are repeated exactly as in (d).
(g)
The
final set of
atmospherics is taken, followed by three sets of "coarse" readings to
complete the
measurement. The
atmospheric readings are exchanged by
the two operators.
4.2.2 Sequential
method of measuring with the MRA-2 Tellurometer
|
|
Master
|
Remote
|
|
(a)
|
Rotate
the Cavity Tune knob for about half a rotation on each side of the previously
decided starting point. If the Remote is not yet switched on to SPEAK only a
small deflection of the needle will be seen. In this case, keep on turning
the control through the above tuning range until the meter deflection becomes large; then carefully tune for maximum deflection, adjusting the CAVITY TUNE and
REFLECTOR TUNE controls.
|
Set
the CAVITY TUNE knob to the previously decided starting point (say 5.0). A
large increase in the reading on the SWITCHED METER indicates that the Master instrument is in contact with the Remote.
|
|
(b)
|
Adjust
the direction of the instrument for maximum AVC reading.
|
Adjust
the direction of the instrument for maximum AVC reading. Listen for any instructions
from the Master.
|
|
(c)
|
Record
the REG
reading.
|
Record
the REG
reading.
|
|
(d)
|
Instruct
the Remote operator to switch to MEASURE. Switch to MEASURE and MASTER A positions. Using the
CIRCLE AMP control, set the circle to a reasonable diameter.
|
When
instructed, switch to MEASURE and Remote A+F positions.
|
|
(e)
|
Adjust
the brightness, focusing, position and shape of the circle. Re-adjust the diameter of the circle.
Make a final adjustment of the REFLECTOR TUNE for a suitable break in the circle. (Failure to obtain any break or a break of suitable width must be treated as an instrumental fault.)
|
Check
the presentation, adjustment.
(BRILLIANCE, FOCUS, X SHIFT, and Y SHIFT.
|
|
(f)
|
Switch
to SPEAK and instruct the Remote operator that "coarse" readings will now be taken. Set the
Speak/Measure switch to MEASURE. Read the angular position (between 0 and 100) of the leading edge of the break
in the circular
trace. (If the circle is traversed in a clockwise direction the first edge of
the break that is encountered is the leading edge). Record this reading and
the A+ reading. Momentarily flick the Speak/Measure switch to indicate to the
Remote that he must change patterns. Take another reading of the position of the leading edge of
the break. Record
this as the A- reading.
|
When
instructed that "coarse" readings are to be taken switch to MEASURE
and either listen to the tone signal, in the earphones or watch the pulse display
on the cathode ray tube. When they disappear momentarily switch to the A-F position.
|
|
(g)
|
Switch
the pattern selector to MASTER B. When the circular trace reappears, take a
reading and
record it
as the B reading.
|
When
the display and tone disappear, switch the pattern selector to REMOTE B.
|
|
(h)
|
Repeat
(g) for the MASTER C and D positions.
|
Repeat
(g) for the REMOTE C and D positions.
|
|
(i)
|
Switch
to CAVITY TUNE 3. Tune to the Remote as motioned in (a). Take a set of coarse readings as
described in (f) to (h).
|
Switch
to CAVITY TUNE 3. When contact is made with the Master, switch to MEASURE and
proceed with coarse readings as described in (f) to (h).
|
|
(j)
|
Switch
to CAVITY TUNE 10. Tune to the Remote as motioned in (a). Take a set of coarse readings as
described in (f) to (h).
|
Switch
to CAVITY TUNE 10. When contact is made with the Master, switch to MEASURE
and proceed with coarse readings as described in (f) to (h).
|
|
(k)
|
Switch
to SPEAK and instruct the Remote operator to take a set of atmospheric
readings. Calculate the vapour pressure, and compare with the Remote to see they come within the allowable
limits.
|
When
instructed take a set of atmospheric readings. Calculate the vapour pressure, and compare with the Remote
to see they come within the allowable limits.
|
|
(l)
|
Inform
the Remote operator that
Fine
readings will
now be taken.
Allow the
Remote operator sufficient time to return to his instrument; then with the REFLECTOR TUNE control
adjust for maximum AVC reading. Switch to MEASURE. Take a reading on the CRT
graticule and record it as the A+F reading. Flick the Speak/Measure switch
and record the next reading as the A-F. Repeat for A-R and A+R.
|
When
instructed by the Master operator that Fine readings will now be taken adjust the REFLECTOR TUNE control for peak crystal current. When instructed
switch to MEASURE. When the tone or the display disappear momentarily switch
to the A-F position. Repeat for A-R and A+R. Note this order must be adhered to unless changed prior
to measuring by the Master operator.
|
|
(m)
|
Switch
to SPEAK get Remote AVC reading. Instruct Remote operator to change
frequency.
Retune
the instrument to its new setting below that of the Remote.
Take
a further
set of 4 "fine"
readings.
|
Switch
to SPEAK report Remote AVC reading, change to the frequency instructed by the
Master operator, switch to A+F and repeat step (l).
|
|
(n)
|
Repeat
step (m) through the tuning range.
|
Repeat
step (m) through the tuning range.
|
|
(o)
|
Take
a set of
atmospheric readings, compare vapour pressure as before.
|
Take
a set of
atmospheric readings, compare vapour pressure as before.
|
|
(p)
|
This
completes
one half of the measurement. The Remote operator now becomes the Master
operator and the measurement proceeds.
|
The
Remote operator
now changes to
Master operator, and the measurement proceeds.
|
The sequence for this
second half of the measurement is in reverse of the first half, the order being
:
(i)
Fine
readings.
(ii) Atmospherics.
(iii) Coarse readings.
Atmospherics are now exchanged, also any data about eccentric or station marks. The
instrument can now be packed away. First switch off the HT, then the LT, disconnect the battery, headset, dipole and reflecting dish.
4.2.3 Operation
over land
Although in principle, any line over which it is possible to
transmit and receive signals, can be measured by the Tellurometer system,
circumstances may be such that a choice of sites for the instrument can be
made. This applies particularly to surveying in country where beacons either do
not exist, or need not be
used. As operation of the instrument at sites with suitable properties may
improve the accuracy and
ease of measurement, some attention should be paid to site selection.
Two factors influence the choice of a line for good working reception
of signals and ground reflection.
In the first place, the line should be free from obstruction, and
the plane of the radio beam (22°
wide), should not be obstructed
for the first 30 metres. This latter point can be ensured by raising the
instrument about 2 metres, if the ground is level; or by selecting a site where
the ground falls
gradually away from the station for at least 30 metres. The terrain should be
free from obstructions such as trees or buildings in a cone of about 10° on
each side of the line. If it is impossible to select a site with this last
requirement it is essential that the trees do not move during the measuring
period. In other words wait for still weather conditions.
In the second place a line should be selected so that the ground
reflection effects are negligible. Since this is not usually possible, the next
best course is to select sites that result in at least one full cycle of swing.
If the ground is well wooded or otherwise broken up, the indirect
ray can be scattered, and not reflected. Even in this event the power of the
indirect ray which reaches the receiver may not be negligibly small. To prevent
the resulting errors it is best to adopt the second procedure above, i.e., to select a line
that has good ground reflection properties and results in at least one cycle of
swing.
Such a line has a ground clearance of about 70 metres over a
distance of
32km, 45 metres over a distance of 16km, and so on. Since more than one cycle
of swing is desirable, sites with clearances at the middle point of over 70
metres for 32km lines, over 45m for 16km lines and over 30m for 8km lines and so on, should be selected.
4.2.4 Operation over water
Certain conditions of a water surface, such as a very choppy sea, can cause scattering of
the indirect ray, in a similar manner to rough ground; but, in general, the
conditions are similar to those of flat, bare ground.
An additional effect from an over water path, is a regular or
irregular change in the length of the indirect ray due to a vertical rise and fall of the surface caused by
"swell". This rise and fall results in a changing of the relative phase of the direct and
indirect rays, in the same way as a change of carrier frequency does. Thus, if the carrier frequency
were kept constant, the readings would nevertheless swing about a mean value;
in principle, it would be sufficient to average this swing, instead of obtaining a swing by
frequency diversity. In practise, however, an operator cannot be certain that a full swing
has been developed, and the method of frequency variation must be carried out.
Since "swell" can introduce errors even though frequency
is employed, sites should be
selected where possible so that the ground obscures the water surface from the
instrument thus there will be no reflection from the water. Sometimes this can
be made possible
by lowering
the instrument.
4.2.5 Atmospheric
effects
The final limiting factor in obtaining maximum accuracy, at medium
and long ranges, is the effect of atmospheric conditions. The procedure set out for
taking atmospheric
readings, can be regarded as being adequate under most conditions. This procedure assumes
that the
atmospheric conditions along the line are constant or vary uniformly. If either condition does not exist, an error in measurement can result.
Since there is no way of determining the atmospheric conditions along the line, the best procedure is to carry out measurements during
periods of certain
weather
conditions.
Fine, dry, sunny weather, which induces vertical air currents are ideal. A fair breeze, blowing
along the line, is to be preferred
to any other type of wind. Night measurements tend to be less accurate than day measurements.
In damp climates measurements on cooler days will be more accurate than those
on warmer days when the vapour pressure may be higher. In coastal areas anomalies may be
experienced due to variations in vapour pressure along the line; however, in general the vapour
pressure is constant
over large areas and changes only slowly with time.
4.3 Field computation of Tellurometer measurements
For the reduction of vapour pressure, dry and wet bulb
temperatures are required, also the barometric pressure.
Tables have been made up so that these can be calculated using Centigrade readings for temperature, and millibar readings for
pressure. See (h)
below. NOTE : The tables in these notes have been constructed with Excel and
final values differ from the original tables above 30 degrees by up to 0.04 due
to evaluation of power term.
Taking the readings :
(a)
The
dry and wet bulb reading of the psychrometer should be taken with the instrument in the shade and at the height of the instrument. The psychrometer should be held well away from the
observer’s body and in a position where the air-vent is pointing into the wind.
The observer should watch the mercury throughout the observation. The mercury sometimes
tends to oscillate, but readings should not be made until the thermometers have
reached their minimum values. It will take 3 or
more minutes
for this to happen.
(b)
The
thermometers are calibrated and the chart showing the index corrections for the
temperature ranges should be kept in the box containing the psychrometer.
(c)
The
time of observation is recorded to the nearest minute and the Master operator enters his wet and dry bulb readings, in
their appropriate column in the field book. The index corrections are then applied, and the final values entered.
(d)
The
results are checked with the Remote operator to see that the vapour pressure, at each end of the line, agrees within
the required limits before "fine" readings are proceeded with.
(e)
The
wick on the wet
bulb should be kept clean, and replaced when dirty. Only clean water should be used.
Be sure no water gets on the dry bulb.
In the Bendix model, care should be taken to ensure that the batteries are in good condition.
(f)
The
barometer should be read immediately after the dry and wet bulb temperatures
have been read. The readings should be recorded in the appropriate places in the field book, index corrections applied, and the final
adopted values shown.
(g)
Barometer
comparisons should be carried out at regular intervals throughout the course of the survey. The
mechanism barometers are compared against a standard mercury barometer at a
Department of Civil Aviation Meteorological Office or other Meteorological
Station.
(h)
Figures
4.3.1(a) & (b) show Tables "A" & "B". These are'
necessary to calculate the Vapour Pressure from the atmospheric readings. A
set of these
tables must be carries with each instrument to enable the calculated vapour pressure at each end of the line to be compared
before and after
each measurement. This is to ensure that they agree within the limits specified for the particular task in
hand. Figure 4.3.2 shows these calculations on the appropriate field book page.
|
TABLE A
|
|
Δe = 0.00066*(1+(0.00115*t'))p
|
|
|
|
|
|
|
|
WET
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BULB
|
Millibars
|
|
Celcius
|
820
|
830
|
840
|
850
|
860
|
870
|
880
|
890
|
900
|
910
|
920
|
930
|
|
0
|
0.541
|
0.548
|
0.554
|
0.561
|
0.568
|
0.574
|
0.581
|
0.587
|
0.594
|
0.601
|
0.607
|
0.614
|
|
5
|
0.544
|
0.551
|
0.558
|
0.564
|
0.571
|
0.578
|
0.584
|
0.591
|
0.597
|
0.604
|
0.611
|
0.617
|
|
10
|
0.547
|
0.554
|
0.561
|
0.567
|
0.574
|
0.581
|
0.587
|
0.594
|
0.601
|
0.608
|
0.614
|
0.621
|
|
15
|
0.551
|
0.557
|
0.564
|
0.571
|
0.577
|
0.584
|
0.591
|
0.598
|
0.604
|
0.611
|
0.618
|
0.624
|
|
20
|
0.554
|
0.560
|
0.567
|
0.574
|
0.581
|
0.587
|
0.594
|
0.601
|
0.608
|
0.614
|
0.621
|
0.628
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25
|
0.557
|
0.564
|
0.570
|
0.577
|
0.584
|
0.591
|
0.597
|
0.604
|
0.611
|
0.618
|
0.625
|
0.631
|
|
30
|
0.560
|
0.567
|
0.574
|
0.580
|
0.587
|
0.594
|
0.601
|
0.608
|
0.614
|
0.621
|
0.628
|
0.635
|
|
35
|
0.563
|
0.570
|
0.577
|
0.584
|
0.590
|
0.597
|
0.604
|
0.611
|
0.618
|
0.625
|
0.632
|
0.639
|
|
40
|
0.566
|
0.573
|
0.580
|
0.587
|
0.594
|
0.601
|
0.608
|
0.614
|
0.621
|
0.628
|
0.635
|
0.642
|
|
45
|
0.569
|
0.576
|
0.583
|
0.590
|
0.597
|
0.604
|
0.611
|
0.618
|
0.625
|
0.632
|
0.639
|
0.646
|
|
|
Millibars
|
|
|
940
|
950
|
960
|
970
|
980
|
990
|
1000
|
1010
|
1020
|
1030
|
1040
|
1050
|
|
0
|
0.620
|
0.627
|
0.634
|
0.640
|
0.647
|
0.653
|
0.660
|
0.667
|
0.673
|
0.680
|
0.686
|
0.693
|
|
5
|
0.624
|
0.631
|
0.637
|
0.644
|
0.651
|
0.657
|
0.664
|
0.670
|
0.677
|
0.684
|
0.690
|
0.697
|
|
10
|
0.628
|
0.634
|
0.641
|
0.648
|
0.654
|
0.661
|
0.668
|
0.674
|
0.681
|
0.688
|
0.694
|
0.701
|
|
15
|
0.631
|
0.638
|
0.645
|
0.651
|
0.658
|
0.665
|
0.671
|
0.678
|
0.685
|
0.692
|
0.698
|
0.705
|
|
20
|
0.635
|
0.641
|
0.648
|
0.655
|
0.662
|
0.668
|
0.675
|
0.682
|
0.689
|
0.695
|
0.702
|
0.709
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25
|
0.638
|
0.645
|
0.652
|
0.659
|
0.665
|
0.672
|
0.679
|
0.686
|
0.693
|
0.699
|
0.706
|
0.713
|
|
30
|
0.642
|
0.649
|
0.655
|
0.662
|
0.669
|
0.676
|
0.683
|
0.690
|
0.696
|
0.703
|
0.710
|
0.717
|
|
35
|
0.645
|
0.652
|
0.659
|
0.666
|
0.673
|
0.680
|
0.687
|
0.693
|
0.700
|
0.707
|
0.714
|
0.721
|
|
40
|
0.649
|
0.656
|
0.663
|
0.670
|
0.677
|
0.683
|
0.690
|
0.697
|
0.704
|
0.711
|
0.718
|
0.725
|
|
45
|
0.653
|
0.659
|
0.666
|
0.673
|
0.680
|
0.687
|
0.694
|
0.701
|
0.708
|
0.715
|
0.722
|
0.729
|
|
FORMULAE
|
:
|
e = e' - (t - t') Δe
|
and
|
|
Δe = 0.00066 *(1+(0.00115* t')) p
|
|
|
|
|
|
|
|
and
|
|
e' = 6.107* (10^ ((7.5* t') / (237.3+ t')))
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where
|
:
|
T
|
is the
|
dry bulb temperature °C
|
|
|
|
|
|
|
|
|
t'
|
is the
|
wet bulb temperature °C
|
|
|
|
|
|
|
|
|
e
|
is the
|
Vapour pressure (millibars)
|
|
|
|
|
|
|
|
e’
|
is the
|
Vapour pressure at saturation (millibars) (Table B)
|
|
|
|
|
|
p
|
is the
|
barometric pressure millibars
|
|
|
|
|
|
|
|
Δe
|
from
|
Table A
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
To find Vapour Pressure e :
|
|
Example :
|
|
|
|
|
|
|
|
|
|
|
|
|
Pressure
|
1010
|
Millibars
|
|
|
|
|
|
|
|
|
|
Dry bulb
|
26.1
|
°C
|
|
|
|
|
|
|
|
|
|
|
Wet bulb
|
24.4
|
°C
|
|
|
|
|
|
|
|
|
|
|
Depression
|
1.7
|
(Dry - Wet)
|
|
|
|
|
(a)
|
Extract value from Table B
|
|
|
|
|
|
|
|
|
|
|
for wet bulb temperature
|
From Table B - wet bulb value extract :
|
30.56
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b)
|
Extract constant from
|
|
From Table A - wet bulb & pressure values extract :
|
0.686
|
|
|
|
Table A and multiply by
|
|
|
multiply by wet bulb depression
|
1.7
|
|
|
|
wet bulb depression.
|
|
|
|
subtract from Table B value
|
1.166
|
|
|
|
Subtract from Table B value
|
|
|
|
e
|
millibars
|
=
|
29.39
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure
4.3.1(a) : Table "A"
|
TABLE B
|
|
|
|
Vapour pressure at saturation - e'
|
|
|
|
WET
|
|
|
|
|
|
|
|
|
|
|
|
BULB
|
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
|
0
|
6.107
|
6.152
|
6.196
|
6.242
|
6.287
|
6.333
|
6.379
|
6.425
|
6.472
|
6.519
|
|
1
|
6.566
|
6.614
|
6.661
|
6.710
|
6.758
|
6.807
|
6.856
|
6.905
|
6.955
|
7.005
|
|
2
|
7.055
|
7.106
|
7.157
|
7.208
|
7.260
|
7.312
|
7.364
|
7.417
|
7.469
|
7.523
|
|
3
|
7.576
|
7.630
|
7.685
|
7.739
|
7.794
|
7.849
|
7.905
|
7.961
|
8.017
|
8.074
|
|
4
|
8.131
|
8.189
|
8.246
|
8.304
|
8.363
|
8.422
|
8.481
|
8.541
|
8.601
|
8.661
|
|
5
|
8.722
|
8.783
|
8.844
|
8.906
|
8.968
|
9.031
|
9.094
|
9.157
|
9.221
|
9.285
|
|
6
|
9.349
|
9.414
|
9.480
|
9.545
|
9.612
|
9.678
|
9.745
|
9.812
|
9.880
|
9.948
|
|
7
|
10.017
|
10.086
|
10.155
|
10.225
|
10.295
|
10.366
|
10.437
|
10.509
|
10.580
|
10.653
|
|
8
|
10.726
|
10.799
|
10.873
|
10.947
|
11.021
|
11.096
|
11.172
|
11.248
|
11.324
|
11.401
|
|
9
|
11.478
|
11.556
|
11.634
|
11.713
|
11.792
|
11.872
|
11.952
|
12.033
|
12.114
|
12.195
|
|
10
|
12.277
|
12.360
|
12.443
|
12.526
|
12.610
|
12.695
|
12.780
|
12.865
|
12.951
|
13.038
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
|
13.125
|
13.212
|
13.300
|
13.389
|
13.478
|
13.567
|
13.657
|
13.748
|
13.839
|
13.931
|
|
12
|
14.023
|
14.116
|
14.209
|
14.303
|
14.397
|
14.492
|
14.587
|
14.683
|
14.780
|
14.877
|
|
13
|
14.975
|
15.073
|
15.172
|
15.271
|
15.371
|
15.472
|
15.573
|
15.674
|
15.777
|
15.879
|
|
14
|
15.983
|
16.087
|
16.192
|
16.297
|
16.403
|
16.509
|
16.616
|
16.724
|
16.832
|
16.941
|
|
15
|
17.050
|
17.160
|
17.271
|
17.382
|
17.494
|
17.607
|
17.720
|
17.834
|
17.948
|
18.063
|
|
16
|
18.179
|
18.296
|
18.413
|
18.530
|
18.649
|
18.768
|
18.888
|
19.008
|
19.129
|
19.251
|
|
17
|
19.373
|
19.496
|
19.620
|
19.745
|
19.870
|
19.996
|
20.122
|
20.250
|
20.378
|
20.506
|
|
18
|
20.636
|
20.766
|
20.897
|
21.028
|
21.160
|
21.293
|
21.427
|
21.562
|
21.697
|
21.833
|
|
19
|
21.969
|
22.107
|
22.245
|
22.384
|
22.524
|
22.664
|
22.805
|
22.947
|
23.090
|
23.234
|
|
20
|
23.378
|
23.523
|
23.669
|
23.816
|
23.963
|
24.111
|
24.260
|
24.410
|
24.561
|
24.712
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21
|
24.865
|
25.018
|
25.172
|
25.327
|
25.482
|
25.639
|
25.796
|
25.954
|
26.113
|
26.273
|
|
22
|
26.434
|
26.595
|
26.758
|
26.921
|
27.085
|
27.250
|
27.416
|
27.583
|
27.750
|
27.919
|
|
23
|
28.088
|
28.259
|
28.430
|
28.602
|
28.775
|
28.949
|
29.124
|
29.300
|
29.476
|
29.654
|
|
24
|
29.833
|
30.012
|
30.193
|
30.374
|
30.556
|
30.740
|
30.924
|
31.109
|
31.295
|
31.483
|
|
25
|
31.671
|
31.860
|
32.050
|
32.241
|
32.433
|
32.626
|
32.820
|
33.015
|
33.212
|
33.409
|
|
26
|
33.607
|
33.806
|
34.006
|
34.207
|
34.410
|
34.613
|
34.817
|
35.023
|
35.229
|
35.437
|
|
27
|
35.645
|
35.855
|
36.066
|
36.278
|
36.490
|
36.704
|
36.919
|
37.136
|
37.353
|
37.571
|
|
28
|
37.791
|
38.011
|
38.233
|
38.456
|
38.680
|
38.905
|
39.131
|
39.358
|
39.587
|
39.817
|
|
29
|
40.048
|
40.280
|
40.513
|
40.747
|
40.983
|
41.219
|
41.457
|
41.696
|
41.937
|
42.178
|
|
30
|
42.421
|
42.665
|
42.910
|
43.156
|
43.404
|
43.653
|
43.903
|
44.154
|
44.407
|
44.660
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31
|
44.915
|
45.172
|
45.429
|
45.688
|
45.948
|
46.210
|
46.473
|
46.737
|
47.002
|
47.269
|
|
32
|
47.537
|
47.806
|
48.076
|
48.348
|
48.622
|
48.896
|
49.172
|
49.449
|
49.728
|
50.008
|
|
33
|
50.289
|
50.572
|
50.856
|
51.142
|
51.429
|
51.717
|
52.007
|
52.298
|
52.590
|
52.884
|
|
34
|
53.180
|
53.477
|
53.775
|
54.075
|
54.376
|
54.678
|
54.982
|
55.288
|
55.595
|
55.903
|
|
35
|
56.213
|
56.525
|
56.838
|
57.152
|
57.468
|
57.785
|
58.104
|
58.425
|
58.747
|
59.070
|
|
36
|
59.395
|
59.722
|
60.050
|
60.380
|
60.711
|
61.044
|
61.379
|
61.715
|
62.053
|
62.392
|
|
37
|
62.733
|
63.075
|
63.419
|
63.765
|
64.112
|
64.461
|
64.812
|
65.164
|
65.518
|
65.874
|
|
38
|
66.231
|
66.590
|
66.951
|
67.313
|
67.677
|
68.043
|
68.410
|
68.779
|
69.150
|
69.523
|
|
39
|
69.897
|
70.273
|
70.651
|
71.031
|
71.412
|
71.795
|
72.180
|
72.567
|
72.955
|
73.345
|
|
40
|
73.738
|
74.131
|
74.527
|
74.925
|
75.324
|
75.725
|
76.128
|
76.533
|
76.940
|
77.349
|
|
|
This table was constructed with Excel and differs from the
original,
|
|
|
|
|
|
above 30 degrees by 0.04, due to evaluation of power term
|
|
|
|
|
Figure
4.3.1(b) : Table "B"
The formulae form which
these tables are calculated are :
e = e’ – (t-t’)*Δe and
Δe = 0.000 66(1+0.00115*t’)p
e’
= 6.107 *10a where a = (7.5t’)/(237.3+t’)
where :
e = Vapour
pressure (millibars)
t = dry
bulb temperature °C
t’ = wet bulb
temperature °C
p = barometric
pressure millibars
e’ = Vapour
pressure at saturation (millibars) (Table B)
Δe =
Table A
Example
:
Wet
bulb 24.4°C, Dry 26.1°C, Pressure 1010.0mbar
Δe = 0.000
66(1+0.00115*24.4)*1010.0 = 0.6853
0.686 from Table A
a
= (7.5*24.4)/(237.3+24.4) = 0.6993
e’
= 6.107x100.6993 = 30.556
30.556 from Table B
e = 30.553
– (26.1-24.4)*0.686 = 29.391
29.390 using Tables
4.3.2 Atmospheric
readings required for the computation
These have been taken
simultaneously, at each end of the line :
(a)
Immediately
before the first "fine" readings were commenced.
(b)
At the
Conclusion of these "fine" readings.
(c)
Immediately
after the next series
of "fine" readings.
Dry bulb, Barometric Pressure and Vapour Pressure for
(a) and (b) at both stations, are meaned and used in calculating the first
measurement.
Dry bulb, Barometric
Pressure and Vapour Pressure for (b) and (c) at both stations, are meaned and used in calculating the second
measurement.
See 4.3.2 for an example
of atmospheric readings and calculation.
4.3.3 Explanation
of the “coarse” figure
Coarse patterns are :
A-B 10 kc/s
pattern 50,000 ft. (15,240 metres)
A-C 100 kc/s
pattern 5,000 ft. ( 1,524 metres)
A-D 1000 kc/s
pattern 500 ft. ( 152.4 metres)
A alone 10 mc/s
pattern 50 ft. ( 15.24 metres)
For lines longer than 50,000ft (15,240 metres) the first
figure must be provided by a rough knowledge of the length of the line :
|
KILOMETRES
|
|
MILES
|
|
0
to 15
|
first
figure
|
0
|
|
0
to 10
|
first
figure
|
0
|
|
15
to 30
|
|
1
|
|
10
to 20
|
|
1
|
|
30
to 45
|
2
|
|
20
to 30
|
2
|
|
45
to 60
|
3
|
|
30
to 40
|
3
|
|
60
to 75
|
4
|
|
40
to 50
|
4
|
|
75
to 90
|
5
|
|
50
to 60
|
5
|
Example of a set of coarse
readings, rough distance between 15 & 30km
A+ 16 A+ 16 A+ 16 A+ 16 (add 100, if necessary)
B 09 C 42 D 75 A- 84
07 74 41
2) 32
16 (should
be close to A+)
"Coarse” figure : 1 0
7 4 16 (first figure is 1 as distance 15-30km)
Example of a set of coarse
readings, rough distance between 30 & 45km
A+ 06 A+ 06 A+ 06 A+ 06 (add 100, if necessary.)
B 75 C 80 D 36 A- 92
31 26 70
2) 14
07 (should
be close to A+)
"Coarse” figure : 2 3
2 7 07 (first figure is 2 as distance 30-45km)
Ambiguous discrepancies in
the difference readings
Assume that the following readings are
obtained :
A+ 16 A+ 16 A+ 16 A+ 16
B 09 C 42 D 78 A- 80
07 74 38 2) 36
A= 18
Considering the A-D
figure, it is
seen that the
8 of the 33
does not readily check with the 1 of the 18. On the other hand, considering the A-C figure, the 4 of the 74 checks with the
3 of the 38; thus it may leave some doubt whether the coarse figures are 07318
or 07418. However, since only 3 needs
to be added to 38 to give 41, a value of which the 1
checks with the 1 of the 13, it can be seen the 33 should be 41, the discrepancy
being due possibly to a alight error in the instrument, or in the reading of
the trace. Then the 4 of
the 74 checks with the 4 of
the 41, and
the 1 of the 41 with the 1 of
the 18. Thus the coarse figure is 07418.
“Bracketing” method to
resolve ambiguities
In the measurement under
discussion the difference readings are :
A-B 07, A-C 74, A-D 38 and A 18.
Proceed as follows;
(i)
Write
down the A-D and A figures on the one line with a bracket in the space between the,
thus : 38 [ 18
(ii) Enter in the centre of the
bracket a figure which consists of the tenths digit of the A-D value, and the tenths digit of the A value :
38 [31 18
(iii) Bracket the figure so obtained with
values 10 above
and 10 below,
thus :
41
38 [31 18
21
The value in the bracket that is closest to the observed value is the true difference
reading, i.e., of the three, 41 is closest to 38. Therefore the A-D coarse digit is 4.
Where it is necessary to carry out this method on the A-C, and A-B
values as
well, always treat
the A-D reading first, then repeat the others, thus :
A+ 16 A+ 16 A+ 16 A+ 16
B 09 C 38 D 18 A- 80
07 78 98 2) 36
A= 18
01√
98 [91 18
81
80√ Step
1
78 [70 01
60
18 Step
2
07 [08√ 80
98
Step
3
Step 1 : The correct A-D
value is 01, therefore use the "0" (tenths digit) in Step 2.
Step 2 : The correct A-C
value is 80,
therefore use the "8" (tenths digit) in Step 3.
Step 3 : The correct A-B value is 08.
The coarse figure
therefore is 08018, which is not readily apparent from the difference readings.
Unresolvable difference
readings
Consider the following set of readings :
A+ 16 A+ 16 A+ 16 A+ 16
B 11 C 37 D 74 A- 76
05 79 42 2) 40
A= 20
The 2 of the 42 (A-D
value) checks with the 2 of the 20 (a value). Using the method of “bracketing”
on the A-C value the following is obtained :
84
79 [74 18
64
However, as 79 is midway between 74 and 84,
the A-C value can either be 74 or 84, and the coarse reading 07420 or 08420.
Provided that there is not too large a difference between the A+
and A values, the A value can be substituted for the A+ value, in evaluating
the, difference readings, thus:-
A+ 20 A+ 20 A+ 20 A+ 16
B 11 C 37 D 74 A- 76
09 83 46 2) 40
A= 20
This gives a coarse figure of 08420 which should be correct.
However to accept these figures would not be good surveying practise, therefore
the coarse figures should be taken again, preferably with a different
instrument.
The cause of ambiguities in the Coarse readings
Assuming the trace has been properly centralised with the
graticule, and the operator has not made a consistent mistake in all 3 sets of coarse readings the cause of an ambiguity
in the readings is that the A+ and A- readings do not approximately total 100.
(The A- reading is an A+ reading taken in a counter-clockwise direction).
Therefore, if the A+ and A- readings usually total in the vicinity
of 92, or 108, or worse, difficulty probably will be found in resolving coarse
readings. If this is the case the instrument should be returned for adjustment.
Care with Coarse readings
A-B crystal gives the value of the distance up to 99,999mμ/s, thus an error of 1 in the
resolving of this coarse figure will give an error of 10,000mμ/s (5000ft
or 1524metres). This is easily traceable from a map.
A-C crystal gives the
value of the distance up to 9,999mμ/s, thus an error of 1 in resolving this coarse figure will give an
error of 1,000mμ/s (500ft or 152metres).
A-D crystal gives the
value of the distance up to 999mμ/s, thus an error of 1 in resolving this coarse figure, will give an
error of 100mμ/s (50ft or 15metres).
An error of 500 feet or less could not be ascertained from the
1:250,000 map which will normally be the most accurate map available for
scaling the check distance. Therefore the correct resolving of the coarse
figures is essential.
4.3.4 Simple
explanation
of the
Tellurometer
measurement
The following is included to enable operators to more readily
comprehend the broad basis of the Tellurometer measurement.
The instrument measures the time taken for a radio wave to travel
from one Station (the Master) to the other (the Remote) and back to the first. The unit of time used is
the millimicrosecond (mμs), which is a thousandth of a millionth of a second.
Suppose the transit time is 10,000 milli-microseconds, i.e., ten
millionths of a second.
As the wave travels about
186,000 miles in one second, in ten millionths of a second it travels :
(186,000 / 1,000,000) * 10
= 1.86 miles.
As this is the double path
length the single path distance is 0.93 miles.
Metric equivalent :
The wave travels about 299,792km in one second, in ten millionths
of a second it travels :
(299,792 / 1,000,000) * 10
= 2.998km.
As this is the double path
length the single path distance is 1.499km.
As the wave travels along the path it meets resistance from the
atmosphere. A correction
is applied for this and the resultant answer is the distance between the stations.
To eliminate any errors from a single
reading (which could be caused by ground reflection), a series of 15 "fine"
readings are taken on successive carrier frequencies.
4.3.5 Booking
and field calculation of a Tellurometer measurement
Figure 4.3.2 shows the atmospheric observation page, vapour
pressure calculations, and the mean of the readings from both stations, as required to calculate the
measurement. The necessary tables to do these calculations should always be carried with each instrument.
Figure 4.3.5.(a) shows the coarse figure and its reduction. Three
sets of coarse readings are taken from each station. A graph of the fine
readings and the description of the quality of the trace are also shown on this
page.
Figure 4.3.5.(b) shows a set of 15 "fine" readings. The
booker receives these from the operator, in the order : A+, A-, A-R, A+R. He can
usually calculate the differences and
fill in these two
columns, as the readings are being taken. The mean differences and the "fine" readings can be quickly
calculated at the conclusion of the measurement. REG and A MOD readings and the
commencement and finishing times
of the measurement, are noted.
The AVC readings at both stations, for each "fine"
reading are noted as the reading is taken. This may be required later on, to
give an idea of the quality of the signal on each cavity.
The 15 cavities are meaned. As a check, all columns can be
totalled and cross-checked, as shown, to also provide the mean of the 15 cavities.
The calculation page of the field book is shown in Figure 4.3.5.(c). This shows the calculation being done
in the following steps :
(i)
Transit
time entered
and halved.
(ii) Half Transit time x 299 7925 gives measured distance,
in metres.
(iii) Atmospheric correction is
worked out, using this formula :
n-1
= [ {77.601*(P+E) / (273+t)} * 10-6] and E = (4744 e) /(273+t)
Referring again to Figure 4:3.5(c) we find the following
atmospheric observations are to be used :
Dry bulb temperature t
= 15.4°C
Vapour pressure e
= 8.218 millibars
Baro. pressure P
= 972.19 millibars
Compute E first :
273 + t (15.4) = 288.4 so
4744 *e (8.218) /288.4 =135.18 = E
P+E = 972.19 +135.18
=1107.37 so 77.601 *1107.37 /288.4 =297.964
Thus the atmospheric
correction for 1,000,000 metres is 297.964; for 100,000 metres it would be
29.796 metres and for 10,000m it would be 2.9796 metres.
The correction for the
above measurement of 14,135.240m is :
297.964
X 10-6 x 14,135.240m = 4.211 metres
Eccentric corrections
It is best to draw a
diagram roughly to scale even though very small. This gives the approximate
correction, but more importantly ensures that the correct sign is used.
The calculation is :
Distance eccentric to
station mark x Cos angle station mark to Distant Station
Where the angle is 0° to 90° and 270° to 360°; correction is
minus.
Where angle is 90° to 270°
correction is plus.
Slope correction
This is rarely needed in the field. The difference height
between the stations is necessary. Calculate with the formula provided :
Slope correction = Diff
Height^2 / 2 * Slope distance
Sea Level correction
Also rarely needed in the
field. Mean height of stations necessary. Calculate with the formula provided :
Sea Level correction =
(Mean height * slope distance) / (R + mean height) where R = 6,378,160m
Chord to Arc correction
Also rarely needed in the field. Tables (4.3.5(g)) are available
and should be carried if precise field computations are to be made. Can be
calculated with the formula provided :
Chord to Arc correction =
Slope distance^3 / (43 * {6,378,160}2)
4.4 Fault
finding procedure
When repairs are being undertaken in the field, certain
precautions should be observed in order to ensure the safety of the personnel
and prevent mistakes that can cause a major break-down of the equipment.
The antenna dipole always should be handled carefully. When the
back cover of the instrument is off and inspections are being made, the power
supply should be switched off. Accidental contact with the klystron circuit
when the power is on can result in a bad electrical shock.
The fault finding procedure as set out, should be applied in
locating faults in the instrument, which has largely been designed to be
self-monitoring. Using the indications on the instrument, all but the most
obscure sources of failure should be apparent without the use of separate
equipment, except perhaps, a general-purpose, high-impedance, DC meter.
Certain types of component failure are to be expected from time to
time in any electrical equipment. As a reasonable safeguard, the instruments
are supplied with spare parts kits for use in the field. These spare parts
should be sufficient for 1000 hours operation.
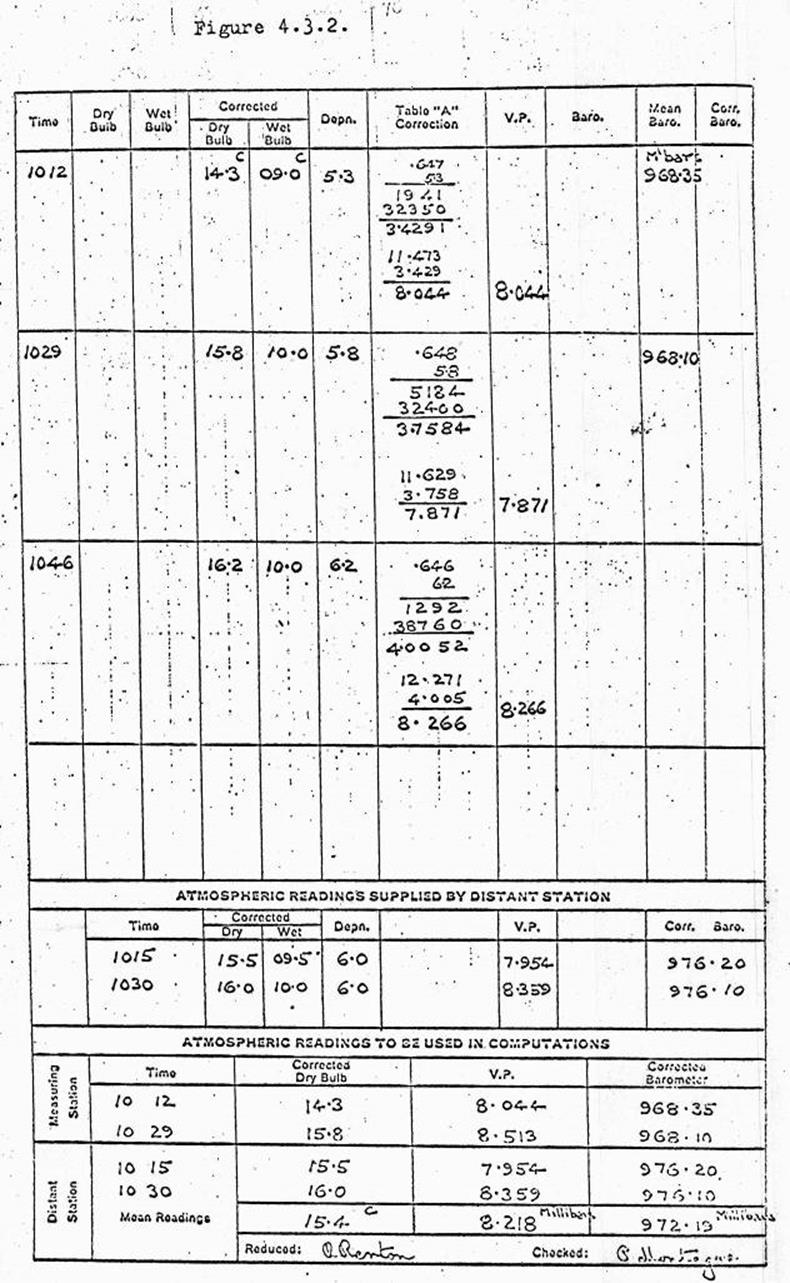
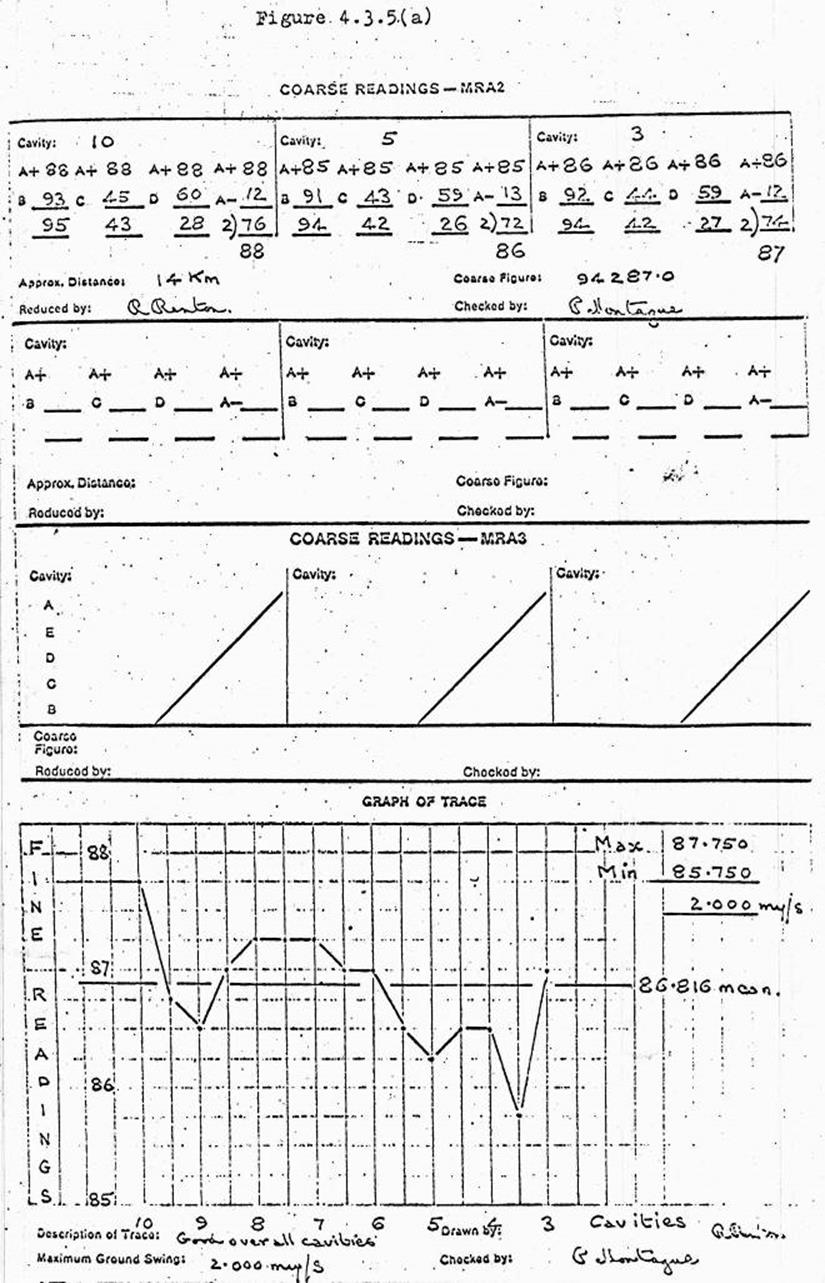
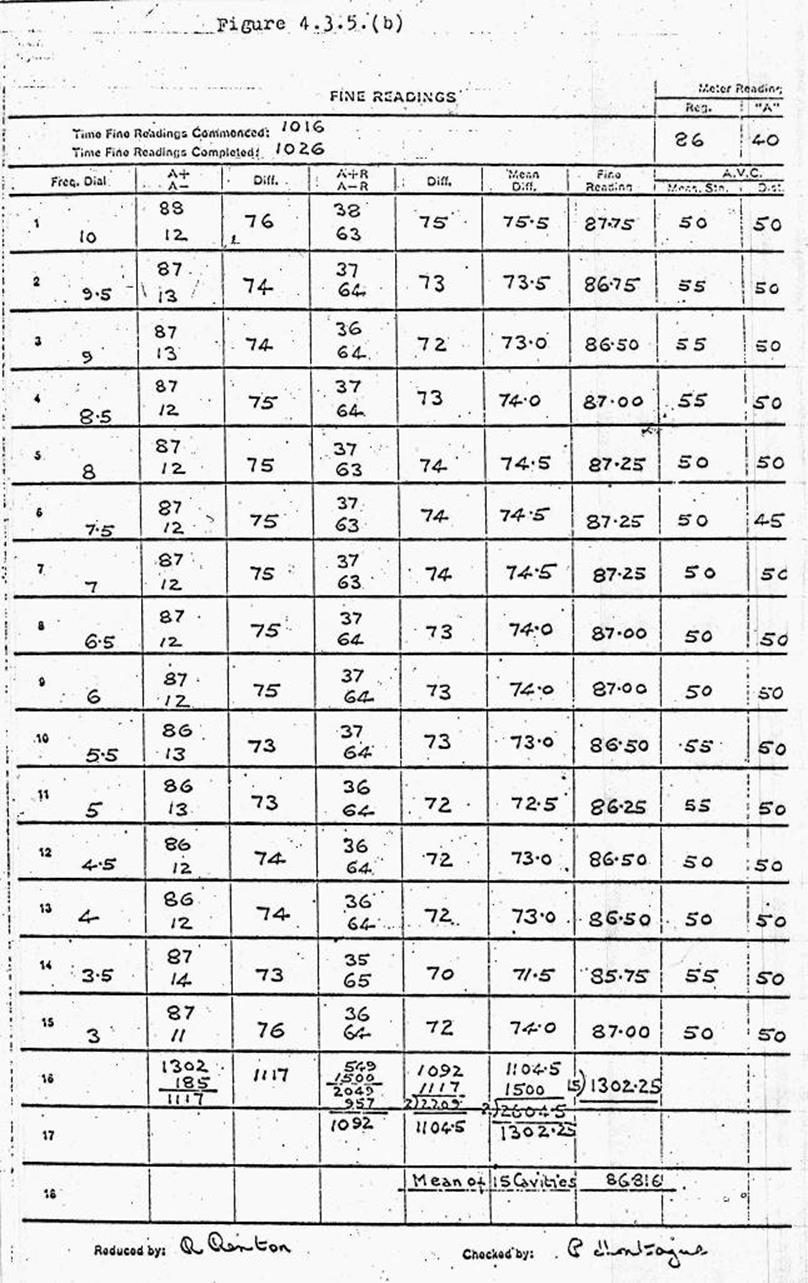
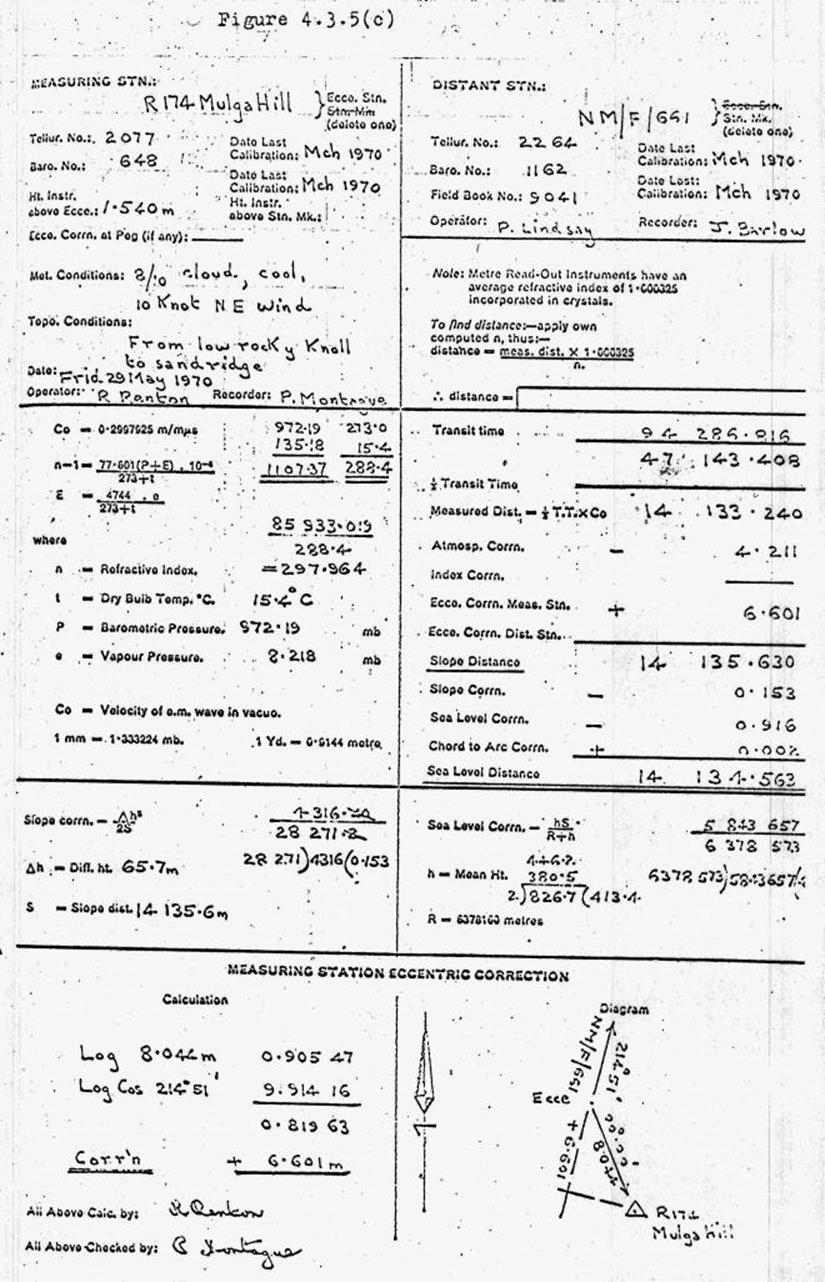
|
CHORD TO ARC CORRECTION TABLES
|
|
|
|
|
|
Chord to Arc correction = Slope distance3 / (43 * {6
378 160}2)
|
|
|
|
All values in metres (slope distances are x1000 metres)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Distance
|
Correction
|
Distance
|
Correction
|
Distance
|
Correction
|
Distance
|
Correction
|
|
10
|
0.001
|
41
|
0.039
|
71
|
0.205
|
101
|
0.589
|
|
11
|
0.001
|
42
|
0.042
|
72
|
0.213
|
102
|
0.607
|
|
12
|
0.001
|
43
|
0.045
|
73
|
0.222
|
103
|
0.625
|
|
13
|
0.001
|
44
|
0.049
|
74
|
0.232
|
104
|
0.643
|
|
14
|
0.002
|
45
|
0.052
|
75
|
0.241
|
105
|
0.662
|
|
15
|
0.002
|
46
|
0.056
|
76
|
0.251
|
106
|
0.681
|
|
16
|
0.002
|
47
|
0.059
|
77
|
0.261
|
107
|
0.700
|
|
17
|
0.003
|
48
|
0.063
|
78
|
0.271
|
108
|
0.720
|
|
18
|
0.003
|
49
|
0.067
|
79
|
0.282
|
109
|
0.740
|
|
19
|
0.004
|
50
|
0.071
|
80
|
0.293
|
110
|
0.761
|
|
20
|
0.005
|
51
|
0.076
|
81
|
0.304
|
111
|
0.782
|
|
21
|
0.005
|
52
|
0.080
|
82
|
0.315
|
112
|
0.803
|
|
22
|
0.006
|
53
|
0.085
|
83
|
0.327
|
113
|
0.825
|
|
23
|
0.007
|
54
|
0.090
|
84
|
0.339
|
114
|
0.847
|
|
24
|
0.008
|
55
|
0.095
|
85
|
0.351
|
115
|
0.869
|
|
25
|
0.009
|
56
|
0.100
|
86
|
0.364
|
116
|
0.892
|
|
26
|
0.010
|
57
|
0.106
|
87
|
0.376
|
117
|
0.916
|
|
27
|
0.011
|
58
|
0.112
|
88
|
0.390
|
118
|
0.939
|
|
28
|
0.013
|
59
|
0.117
|
89
|
0.403
|
119
|
0.963
|
|
29
|
0.014
|
60
|
0.123
|
90
|
0.417
|
120
|
0.988
|
|
30
|
0.015
|
61
|
0.130
|
91
|
0.431
|
121
|
1.013
|
|
31
|
0.017
|
62
|
0.136
|
92
|
0.445
|
122
|
1.038
|
|
32
|
0.019
|
63
|
0.143
|
93
|
0.460
|
123
|
1.064
|
|
33
|
0.021
|
64
|
0.150
|
94
|
0.475
|
124
|
1.090
|
|
34
|
0.022
|
65
|
0.157
|
95
|
0.490
|
125
|
1.117
|
|
35
|
0.025
|
66
|
0.164
|
96
|
0.506
|
126
|
1.144
|
|
36
|
0.027
|
67
|
0.172
|
97
|
0.522
|
127
|
1.171
|
|
37
|
0.029
|
68
|
0.180
|
98
|
0.538
|
128
|
1.199
|
|
38
|
0.031
|
69
|
0.188
|
99
|
0.555
|
129
|
1.227
|
|
39
|
0.034
|
70
|
0.196
|
100
|
0.572
|
130
|
1.256
|
|
40
|
0.037
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4.1 Faults common to the
Master and Remote Functions
Complete failure of the
instrument
If the Oven Cycle lamp is not burning, check the connections to
the battery. Check the LT fuse. Check that the battery is charged.
No noise in the earphone,
but a spot on the CRT.
Check the HT fuse and
replace, if necessary.
No crystal current
Replace the crystal mixer
in the end of the dipole assembly.
Check whether the klystron heater is glowing. If it is not,
replace the klystron. To do this, first switch off the instrument and
disconnect it from the battery. Turn the Cavity Tune control completely
anti-clockwise, and remove the back cover of the instrument. Disconnect the
leads to the klystron. Slacken both retaining rings of the cavity (that at the
base end of the klystron, first) and slide the klystron out of the cavity, and
towards the antenna boss. Reverse the procedure when inserting a new klystron.
No AVC reading, no speech
communication, no pattern on the CRT
Check whether the heaters of all the IF tubes are glowing.
Replace any defective tube.
Low AVC reading, no speech
communication, no pattern on the CRT
Check that the antenna is
directed towards the other instrument.
No speech communication
but instrument operates on measure
Check that the headset
plug is fully inserted in its socket.
Normal AVC reading, normal
speech, 1kc/s note in earphone but no pattern on the CRT
Check brilliance control.
Check tubes V301 and V302
by replacement.
Replace CRT.
No pattern on the CRT, no
1kc/s note in earphone, but speech normal
Check that the pattern
selector is set to the correct position.
Check that the pattern selector of the second instrument is set to
the correct pattern.
Set the Meter switch to MOD and check all the levels. If these
levels are zero on all patterns, check V202 and V203 by replacement
Horizontal deflection but
no vertical deflection on the CRT
Replace V303.
4.4.2 Faults peculiar to the
Master Function
No circle, but speech and
1kc/s note are normal
Adjust the Circle Amplitude control in case the diameter of the
circle is larger than the CRT screen.
Increase the Brilliance.
Follow checks listed in
4.4.1(h)
No phase indicating break,
but circle, 1kc/s note and speech are satisfactory
Press Check Pulse button
and view the CRT.
Adjust the Reflector Tune
control for maximum height of the pulse trace.
If the maximum pulse height is 6mm (¼") or more, release the Check Pulse
button and view the circular trace. If no break is evident reduce the
brilliance to the minimum usable level.
If the maximum pulse height is less than 6mm (¼"), check whether the pulse is
indicated on the Remote CRT. If it is, increase the Remote pulse amplitude.
If no pulse trace is obtained, replace V201. If the fault
persists, check the Remote, according to 4.4.3.(b).
Circle cannot be centred
on the CRT
In the higher magnetic latitudes this fault is probably caused by
the strong vertical magnetic intensity. If that is the case, an adjustment to
the CRT divider chain must be made in an approved Maintenance, Depot before the
instrument can be satisfactorily used. All MkII instruments have had this
adjustment incorporated.
4.4.3 Faults peculiar to the Remote Function
No horizontal trace but a
vertical trace on the CRT
Check tubes V301 and V302,
by replacement.
No pulse display on the
CRT
Check tube V201, by
replacement.
Check tube V303, by replacement.
4.4.4 Anomalous CRT displays
In certain circumstances the trace on the Master CRT may not have
the ideal form.
Mistuning of the klystron cavity produces a triangular display.
Tuning should always be carried out when the Speak/Measure switch is set to
Speak.
An elliptical pattern on one position of the pattern selector
switch indicates that particular pattern frequency needs to re-adjusted in a
Maintenance Depot. Such a pattern should not be read.
A distorted circle can be caused by too large a pulse. If the
reducing of the Remote pulse amplitude does not cure the fault, the instrument
should be returned to a Maintenance Depot. However, an instrument with this
fault can be used, for no reading error is introduced by the distortion.
Multiple circles are caused by either fluorescent lights, when the
instruments are being checked indoors, or engine ignition if the instrument is
connected to the battery of a car whose engine is left running. This display
also can be caused by a defective power pack.
Multiple concentric circles (i.e., circles that change diameter
without altering the angular reading of the break) may be caused either by
reflections from a moving object or by heat refraction on lines with low ground
clearance over the entire distance. Such a display may be read without error.
Rotation of the break backwards and forwards round part of the
circle may be caused by reflected signals from a moving object,that are
stronger than the direct signal.
"Snow" is caused by scattering of the signal by moving
leaves in the line of sight.
A "noisy" or "grassy" display is usually
caused by weak
signals. It can
also be caused by a defective power pack. Provided that the break is evident,
its position can be read without error. Reducing the CRT brilliance to the
lowest usable level helps to clear the break.
4.4.5 Trouble shooting
The charts (Figures 4.4.5(a) and (b) outline the course to be
taken in the event of a failure of the equipment during operation in the
field. It must be stressed that any fault that is not given here must be
rectified in a Maintenance Depot.
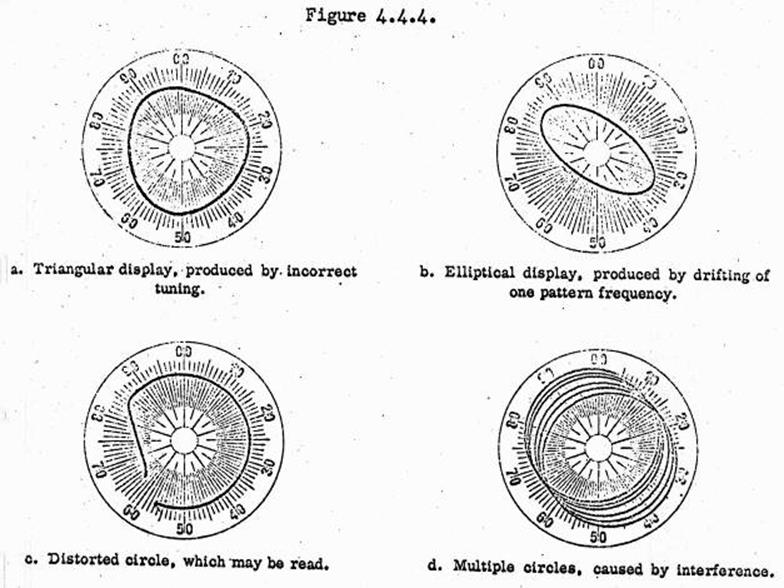
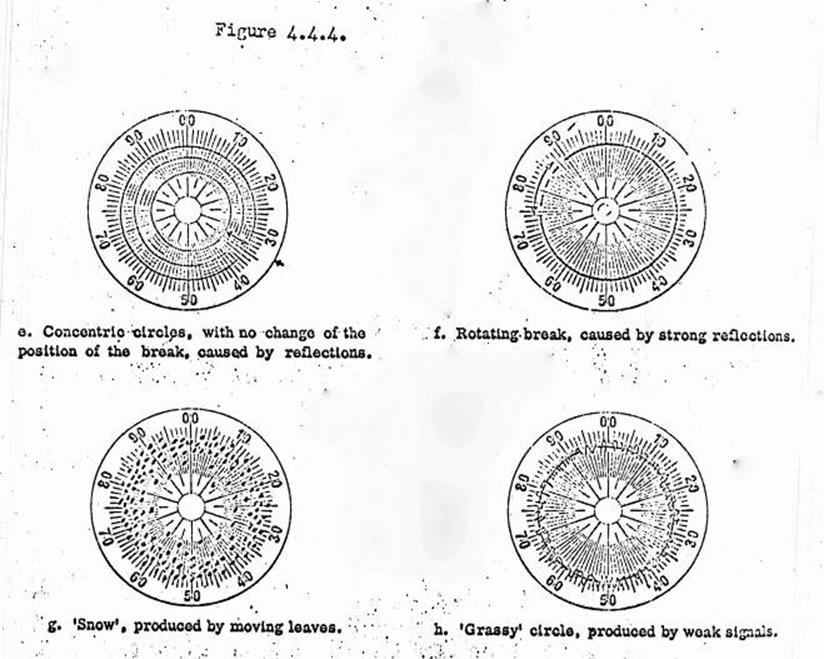
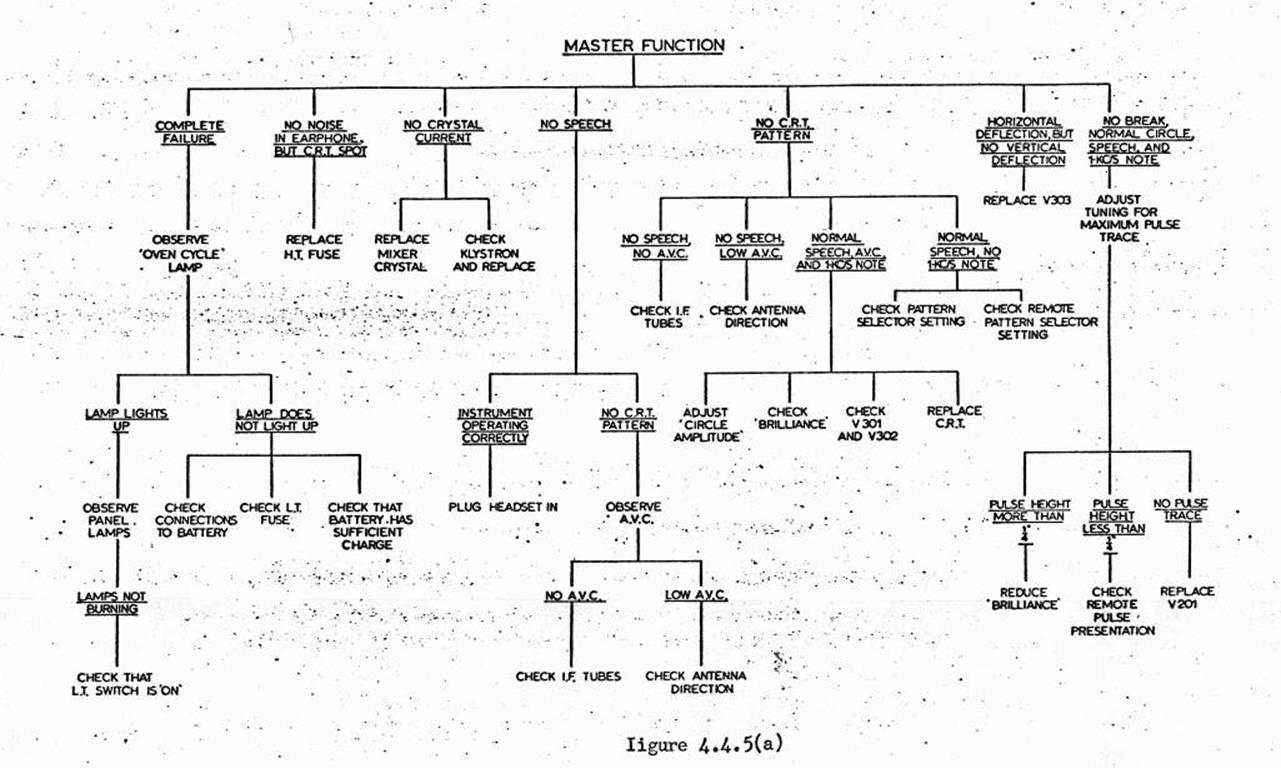
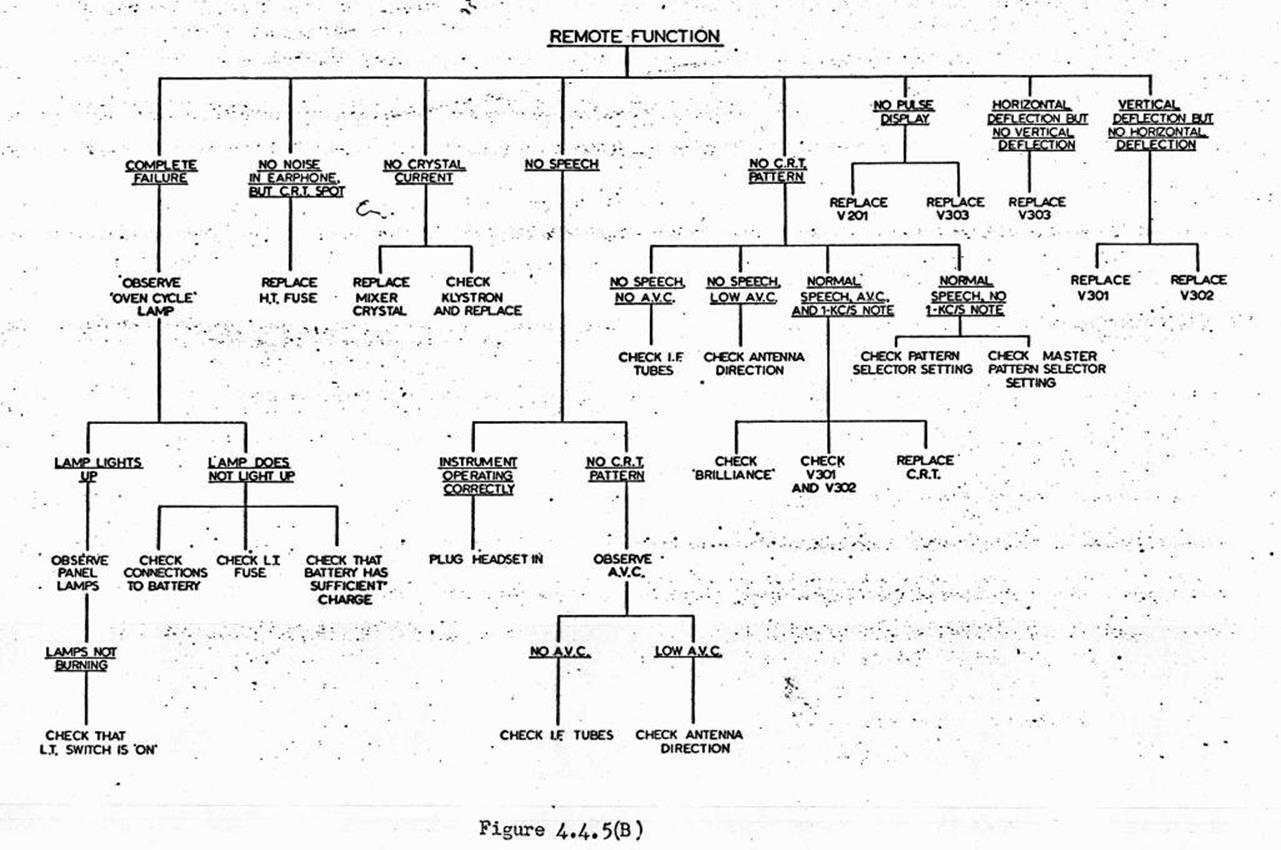
4.5 Tellurometer
MRA-3, Dial read-out Unit – 10m/Hz Instrument
4.5.1
General
Principles
With a pattern frequency of 10m/Hz (previously 10mc/s), one
complete rotation of the Phase Control and the Phase Indicator (0-100 divisions
on the main scale) represents a change of 100 nano-seconds (previously
milli-microseconds) in the transit time over the double path. Each division
therefore, represents one nano-second and is equivalent to a distance of just
under 6 inches (15cm), a complete rotation
of phase being approximately equivalent to 50 feet (17m approx).
The 10m/Hz pattern, or A pattern, thus indicates the final digits
in the transit time in nano-seconds, the preceding figures whole number of
rotations of the A pattern being unknown. These are resolved by providing four
further patterns. The pattern frequencies are :
A Pattern 10.000m/Hz
B Pattern 9.999m/Hz
C Pattern 9.990m/Hz
D Pattern 9.900m/Hz
E Pattern 9.000m/Hz
The Remote frequencies
differ from these by 1k/Hz.
The differences between the readings from the A pattern and the B, C, D and E,
patterns, respectively give phase readings relative difference frequency of the
modulations, and thus coarse patterns are derived, from which the preceding
figures are determined. These coarse patterns, together with the A pattern, are
shown in the following table.
|
A
– B
|
1
k/Hz pattern
|
500
000 ft
|
|
A
– C
|
10
k/Hz
|
50
000 ft
|
|
A
– D
|
100
k/Hz
|
|
5
000 ft
|
|
A
- E .
|
1
m/Hz
|
|
500
ft
|
|
A
alone
|
10
m/Hz
|
|
50
ft
|
See 4.5.3 for the conversion of
transit time to distance.
4.5.2 Simplified theory of measurement
The following is a simplified theory of measurement is included in
these notes to enable operators to readily comprehend the broad basis of the
Tellurometer system. The five difference patterns can be represented by five
wheels, namely the A, B, C, D, and E wheels. Imagine that the circumference of
each wheel is marked by ten equally spaced divisions, and all the wheels rotate
together along a given path. Consider each wheel in turn.
A Wheel
As this wheel is rotated along the path, the circumference
divisions of the wheel indicate the distance traversed. When a complete
revolution is made by the wheel, ten units of distance are indicated by the divisions. When the
wheel is further rotated, the indications of distance continue, but the
observer cannot determine the preceding number of completed revolutions, and is
therefore unable to evaluate the total distance. In order to do this it is
necessary to have a second wheel - the E wheel.
E Wheel
The circumference of the E wheel is ten times greater than that of
the A wheel, therefore the circumferential length of each of its ten divisions
is equal to the whole
circumferential length of the A wheel. When the A wheel has made one
revolution, the E wheel will have traversed the path of one division.
Consequently; when the A wheel has rotated through ten revolutions, the E wheel
will have moved through only one revolution, and will thus measure the length
of the path in terms of 100 A division units.
When the E and
A wheels are further rotated along the path, the observer will again be unable
to determine the preceding number of complete E wheel revolutions, and so it is
necessary to add three further wheels to complete the system.
D, C and B Wheels
The D wheel has a circumference that is ten times greater than
that of the E wheel; therefore the same principle applies for determining the E
wheel revolutions by observing the D wheel division marks, as described for the
E and A wheels.
Two further wheels complete the system. These are the C having a
circumference ten times greater than that of the D wheel, and the B, with a
circumference ten times greater than that of the C wheel.
Thus by observing the division marks on all five wheels the
distance along the path can be determined in terms of A wheel divisions. The A
wheel measures the units of length, and the E, D, C, and B wheels measure the
tens, hundreds, thousands, and tens of thousands of A units, respectively.
4.5.3 Conversion of Time to
Distance
Suppose the transit time is 10 000 nano-seconds, i.e. ten
millionths of a second. As the wave travels approximately 299,792km per second,
in ten millionths of a second it travels :
(299 792 / 1 000 000) * 10 = 2.998 Km which is double path
distance.
Thus the single path distance is 1.499 Km. In other words,
distance = ½Velocity x transit time.
If the velocity is considered constant, the wheels can be
calibrated directly to distance units. However, the velocity varies slightly
with the atmospheric refractive index, in the following manner, therefore for
results of the highest accuracy corrections to the velocity must be made from a
knowledge of the refractive index.
Thus, actual velocity =
(299792 / refractive index) km/s.
4.5.4 Zero
error
The coarse readings, (A, B, C, D, and E) being difference
readings, are free from errors produced by constant phase shift in the
instrument.
An error can arise from contamination of the measuring signal
derived in the Master unit by the measuring signal returned from the Remote,
and vice versa. To eliminate this error, a simple reversal of phase by 180° is
provided by the forward/reverse switch. This is the equivalent of taking face
left and face right readings on a theodolite.
4.5.5
The
Control Panel — Description and location of components
Fuse
Rated at 5A and situated at lower left of panel, protects
instrument against serious damage in event of component failure, or reversing of battery polarity.
Oven lamp
Indicates when crystal oven heater is on. Periodic switching indicates that the oven is being maintained at correct temperature.
Panel lamps
Used to illuminate the panel for night time operation.
Open vents lamp
Red lamp, is situated at the tog left of the panel; it lights if the internal
temperature exceeds 50°C. When lamp lights, the operator should pull open the
two vents at the top and bottom of the radome cover; these should be left open until the
instrument is switched off.
Power switch
Five position switch, is situated towards the lower left hand corner
of the control panel, and can be set to permit operation from either an
internal or an external battery. "Warm Up" brings into use the (12V)
supply to the crystal oven and the LT power pack. "On" brings into
use the HT power pack.
Monitor switch
Six position switch, on lower right hand side of the panel; is
used for monitoring purposes. By means of this switch, the battery volt (Batt),
mixer crystal current (Xtal), received signal strength (AGC) tuning level
(Tune), and modulation levels of the oscillator crystal (Mod), can be indicated
on the Monitor meter, which is situated at the top left of the panel. When the
switch is in the Speak or Measure positions, it is used to select the speech
measure functions of the instrument.
Master/Remote function
switch
Multi-position switch, which is situated at the left hand side of
the panel; is used for selecting the pattern frequency and Master/Remote
function during the measuring process.
AGC switch
This two position switch allows a voltage to be applied to the
klystron for automatically controlling the carrier frequency relative to the other
instrument.
Forward/Reverse switch
Two position switch used for selecting forward and reverse signals
in the elimination of instrumental errors.
Headset connector socket
Marked Mic, and accepts
headset plug.
Battery connector socket
Marked Batt, and connects
12 volt external battery.
Volume control
Marked Vol, and is used
for adjusting level of sound in the headset.
Panel lighting control
Marked Dim, and is used
for adjusting the illumination of the panel.
Cavity tune control
In conjunction with the indicator above, it is used for selecting
the cavity frequency.
The indicator will vary between 000 and 200.
Monitor meter
Situated in the top left hand corner of the panel. This meter is
used in conjunction with the
Monitor switch as previously explained.
Read-out units
These are plug in units and are situated on the upper right hand
side of the control panel. The one in general use within the Division is the
Dial Read-Out unit in nano-seconds. This is the unit to which these operational
notes apply.
4.5.6
Dial Readout Unit (nanoseconds)
Description
The Phase-control Knob is centred on a circular main scale which
is graduated in 100 equal divisions; every tenth division from zero upwards is
numbered in a clockwise direction around the face of the dial. A fixed pointer with vernier scale is
mounted centrally, on top of this main scale. The main scale can be rotated against the
pointer by turning the Phase-control Knob. The vernier scale indicates the
fraction (in tenths of a division), with respect to any whole division on the main scale. There is a
"white dot" on the Phase-control Knob.
A light friction drive is provided between the Phase- control and
the main scale permitting the scale to be held stationary while the
Phase-control is rotated. When a locking device, which is located on upper left
quarter of the disc, is engaged with a notch in the rim of the disc, the main
scale is held in the position indicating zero on the vernier.
The Null meter is mounted above the Phase-control, panel
illumination lamps are provided, one on each side of the meter.
Figure 4.5.(a) shows the operating panel of the MRA-3 Tellurometer
with this dial read-out unit.
Operation
These notes outline the general operation of the dial read-out
unit, the method of fitting this operation into an actual measurement is laid
down in the section, "Sequential method of operating the MRA3
Tellurometer."
At a given Cavity Tune setting, a null position is obtained. By having zero on the main scale locked
against the pointer, the null position is then used as a reference against
which subsequent readings are taken, thus eliminating the need for numerical
subtraction of one reading from the other.
Step 1 Obtaining the null
position
Bring the locking device into contact with the rim of the main
disc by sliding the button towards the centre of the disc.
Rotate the Phase-control knob, either clockwise or anti-clockwise
until the locking device engages with the notch in the rim of the main scale
disc, and the disc is held stationary. The main scale is then set with zero
against the vernier pointer.
Continue to rotate the Phase-control knob until the needle of the
Null meter is in the centre of its scale, (the Null position.)
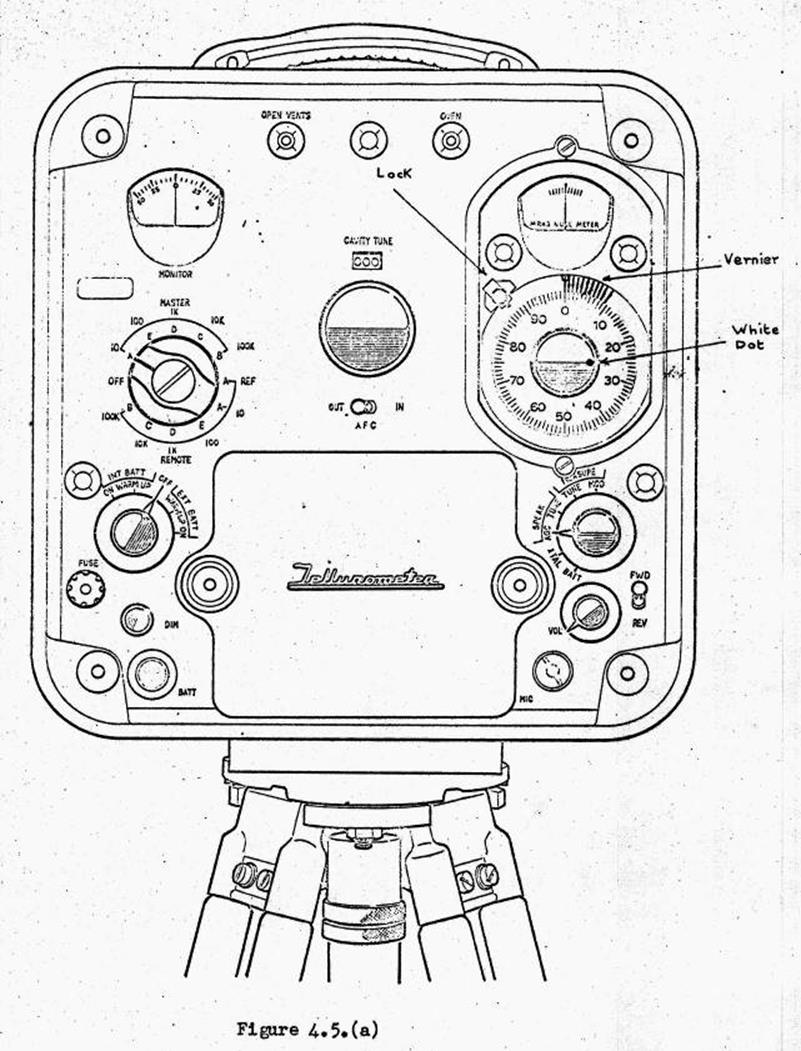
Note : It is possible to obtain two null positions 180°,(or 50
scale divisions) apart. Only one of these positions is correct. When a
clockwise rotation of the Phase-control knob causes the meter needle to move
clockwise; (or an anti-clockwise rotation causes the needle to move
anti-clockwise), the Null position is the correct one. When a rotation of the
Phase-control knob causes the needle to move in the opposite sense, the
position in the incorrect one. The correct condition for a Null reading is therefore obtained by a
continued rotation
of the Phase-control knob in clockwise, (or an anti-clockwise) direction, until
the movements of the Phase-control knob and the meter needle are in the same
sense.
Now book the reading of the position of the "white dot". This
reading is the approximate “A” reading, and is a check against taking readings
50 cycles, i.e,
180° in
error.
Step 2 Obtaining a reading
Disengage the main scale by sliding the button of the locking
device away from the disc. The main scale will now rotate with the
Phase-control knob.
Rotate this knob until a
Null is obtained on the Null meter.
The correct Null position is only obtained when the needle of the Null meter
moves up to the Null position in the same sense as the direction of rotation of
the Phase-control knob, irrespective of whether that knob has been rotated
through a complete revolution or not.
When the needle of the Null meter is in its Null position read the
main scale division which is opposite the pointer, then the decimal part of the
division against the vernier. Record the value read, in the appropriate column
of the field book.
Figures 4.5.(b), (c), (d) and (e) show the pages of a fie book and
include the field computation of the measurement.
4.5.7
Making
contact, preliminary arrangements
It should be noted that this instrument is much more directional
than the MRA-2 Tellurometer; therefore arrangements for making contact should
include :
(i)
Ascertaining
as accurately as possible the bearing of the distant station.
(ii) Time, make contact.
(iii) Which operator is to be
Master.
(iv) On which cavity, contact
is to be made; (normally cavity 100).
(v)
Procedure
for a radio call in the event of failure to make contact by Tellurometer.
4.5.8
Sequential method of operating the MRA-3 Tellurometer
Checking instruments -
Master & Remote, identical procedure
(i)
Set
power switch to EXT BATT/WARM UP.
(ii) Five or ten minutes later
move switch to ON.
(iii) Set MONITOR switch to
BATT; Monitor meter should read between 20 a 25 if battery is sufficiently
charged.
(iv) Set MONITOR switch to
MEASURE/MOD; rotate MASTER/REMOTE switch to patterns. Meter should indicate between 40 and 45 for all patterns except
MASTER E and
REMOTE E where it
should be between 30 & 35.
(v)
Set
MONITOR switch to SPEAKGC.
The sequence, which from hereon differs between Master & Remote is as
follows :
|
MASTER
|
REMOTE
|
|
Making contact
|
|
AFC
switch to IN
MASTER/REMOTE
switch to A MONITOR switch to SPEAKGC
CAVITY
TUNE to 065. Rotate control towards 100, watching for maximum deflection of
MONITOR meter. This normally occurs about 15 below REMOTE i.e., about 35 in
this case.
Make
speech contact.
|
AFC switch to
OUT
MASTER/REMOTE switch to A+ REF MONITOR switch to SPEAKGC
CAVITY TUNE to 100. Listen & watch MONITOR meter; when its
reading moves from a low to high value, contact has been made by Master.
Speech can now heard.
|
|
Instruct
REMOTE to DF his instrument to improve signal strength.
|
When
instructed, DF to obtain maximum deflection on MONITOR meter. Check plumbob is
still over station mark. Advise MASTER when completed.
|
|
DF
Master instrument to obtain maximum deflection on MONITOR meter. Check
plumbob is still over station mark.
|
Stand
by
|
|
Set
MONITOR switch to SPEAK/TUNE and adjust CAVITY TUNE control for a zero, (+ 5)
, reading on the MONITOR meter; check that equal and opposite rotations of
this control result in equal and opposite deflections of the meter needle.
|
Stand
by
|
|
Check
for periodic switching of the Oven lamp.
|
Check
for periodic switching of the Oven lamp.
|
|
Taking
"coarse" readings
|
|
Instruct
REMOTE to switch to MEASURE/ TUNE. Set MONITOR switch to MEASURE/TUNE check
MASTER/REMOTE switch is on MASTER A. Adjust CAVITY TUNE control for a zero,
(±5), reading on the MONITOR meter.
|
When
instructed, set MONITOR switch to MEASURE/TUNE, check MASTER/REMOTE switch is
on REMOTE A+ REF, and FORWARD/REVERSE switch on FWD, (switch is normally
spring-loaded to stay on FWD on most instruments).
|
|
Obtain
NULL point. (See 4.5.6. Step 1) and record position of "white dot".
|
Stand
by
|
|
Switch,
momentarily, to MASTER E and then back to MASTER A, to signal to REMOTE.
|
When 1k/Hz
tone in headset is interrupted, switch to REMOTE A‑
|
|
Obtain
reading, (see 4.5.6. Step 2.) Call to booker who records and calls back.
|
Stand
by
|
|
Switch
to MASTER E
|
When 1 k/Hz tone in headset is interrupted, switch to REMOTE E
|
|
Obtain
and book E reading
|
Stand by
|
|
Switch
to D, C,
& B, in turn, obtaining and booking readings.
|
Switch to D,
C, & B, in turn, on interrupted tone signal.
|
|
Switch
to MASTER A and check first reading.
|
Switch to REMOTE A- to check first reading.
|
|
MONITOR
switch to SPEAK/TUNE.
|
MONITOR
switch to SPEAK/TUNE when Master speaks.
|
|
Instructs
REMOTE to cavity for next set of "coarse" readings. (Usually Cavity
170, then 40.)
MONITOR
switch to SPEAKGC; rotate CAVITY TUNE towards 170, watching for maximum
deflection of monitor meter.
Make
speech contact.
|
MASTER/REMOTE
switch to A+ REF, MONITOR switch to SPEAKGC, CAVITY TUNE to 170. Listen &
watch MONITOR meter; when its reading increases from a low to high value
contact has been made and speech can be heard.
|
|
Set
MONITOR switch to SPEAK/TUNE and adjust CAVITY TUNE for a zero,(±5), reading
on the MONITOR meter; check that equal and opposite rotations of this control
result in equal and opposite deflections of the meter.
|
Stand by
|
|
Master
and Remote now follow previously outlined steps for taking "coarse”
readings until the "coarse" readings on Cavity 170, and the other
necessary cavity are completed. The Master then arranges for simultaneous
atmospheric readings.
|
|
Taking "Fine"
readings
(Assuming
last "coarse" reading was on cavity 40, fine readings will start
with that cavity.)
|
|
Instruct
REMOTE that "Fine" readings will be taken. Switch to MASTER A &
MEASURE /TUNE, readjust CAVITY TUNE for a zero, (±5) reading on the MONITOR
meter.
|
When
instructed, switch to REMOTE A+ REF and MEASURE/TUNE. FORWARD/ REVERSE switch
on FWD.
|
|
Obtain
NULL point (Step 1, 4.5.6. except unnecessary to record position of white
dot.)
|
Stand
by
|
|
Interrupt
tone to signal to REMOTE by momentarily switching to MASTER E and back to
MASTER. A.
|
On
hearing interrupted tone, switch to REMOTE A-
|
|
Obtain
readings (Step 2, 4.5.6).
Call
reading to booker who records and calls back.
|
Stand
by
|
|
Signal
to REMOTE
|
On
hearing signal, switch to REMOTE A+ REF, and hold FORWARD/REVERSE switch down
on REV.
|
|
Obtain
NULL point, as previous.
|
Stand
by
|
|
Signal
to REMOTE
|
On
signal, switch to REMOTE A- keeping FORWARD/REVERSE switch down on REV.
|
|
Obtain
reading, as previous.
|
Stand
by
|
|
Switch to
SPEAKGC and instruct (or signal) REMOTE to change to next cavity.
|
On
instructions (or signal), let FORWARD/REVERSE switch spring back to FWD;
switch to REMOTE A+ REF. Set MONITOR SWITCH to SPEAKGC. CAVITY TUNE to next
setting (in this case, 50).
|
|
Rotate CAVITY
TUNE through increasing numbers until a peak reading is obtained on the
MONITOR meter. This occurs normally at about 15 below the REMOTE, i.e., about 35 in
this case. Set MONITOR SWITCH to SPEAK/TUNE and adjust CAVITY TUNE to
obtain a zero, (±5), reading on the MONITOR meter.
|
Stand
by
|
|
Instruct REMOTE to switch to MEASURE/TUNE. Set MONITOR switch
to MEASURE/TUNE and readjust CAVITY TUNE for a zero, (±5), reading on the MONITOR
meter.
|
Change to
MEASURE/TUNE.
|
|
Master
and Remote now follow previously outlined steps for taking "Fine"
readings, until
they are
completed on this cavity and the other necessary cavities. Simultaneous atmospheric readings
are then arranged by the Master.
|
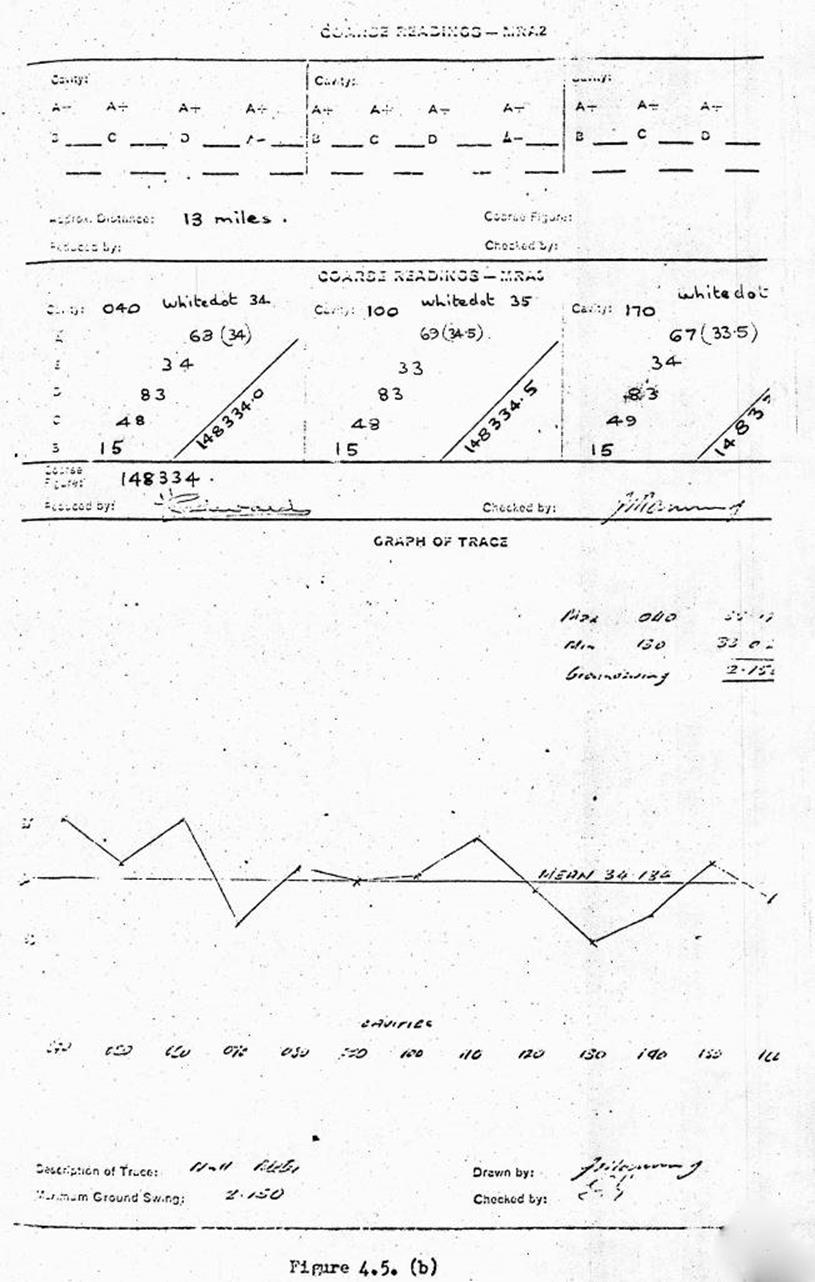
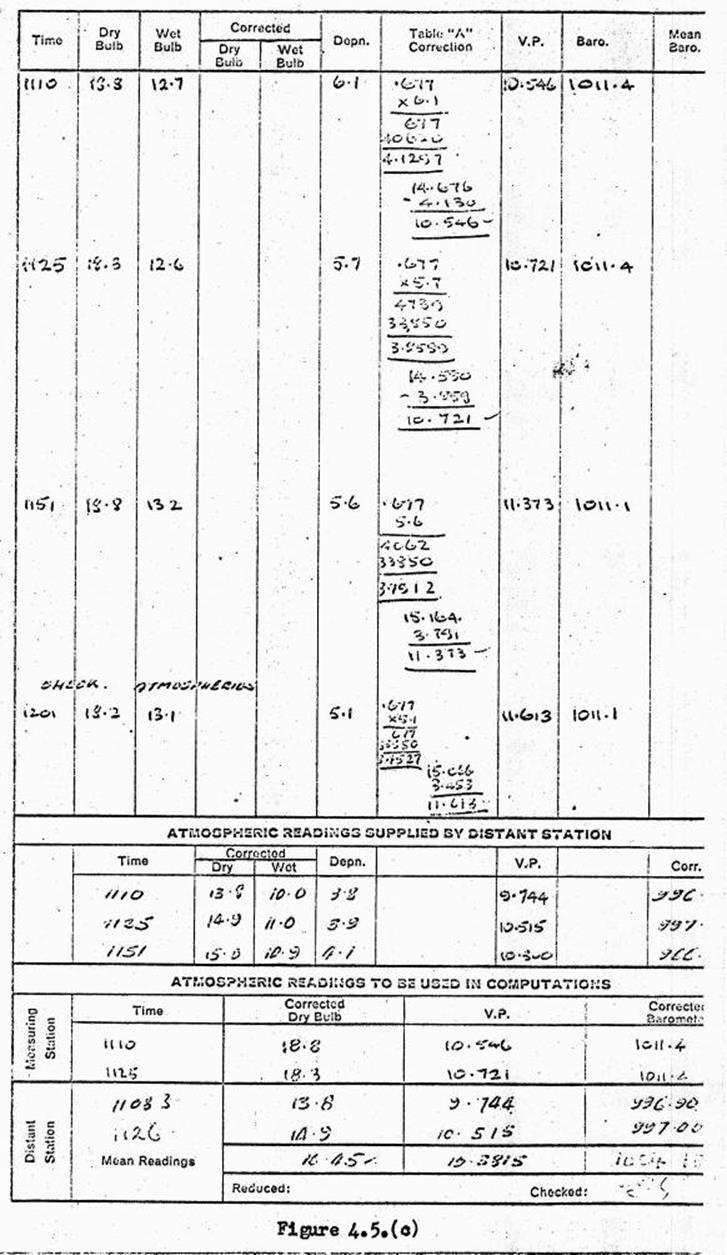
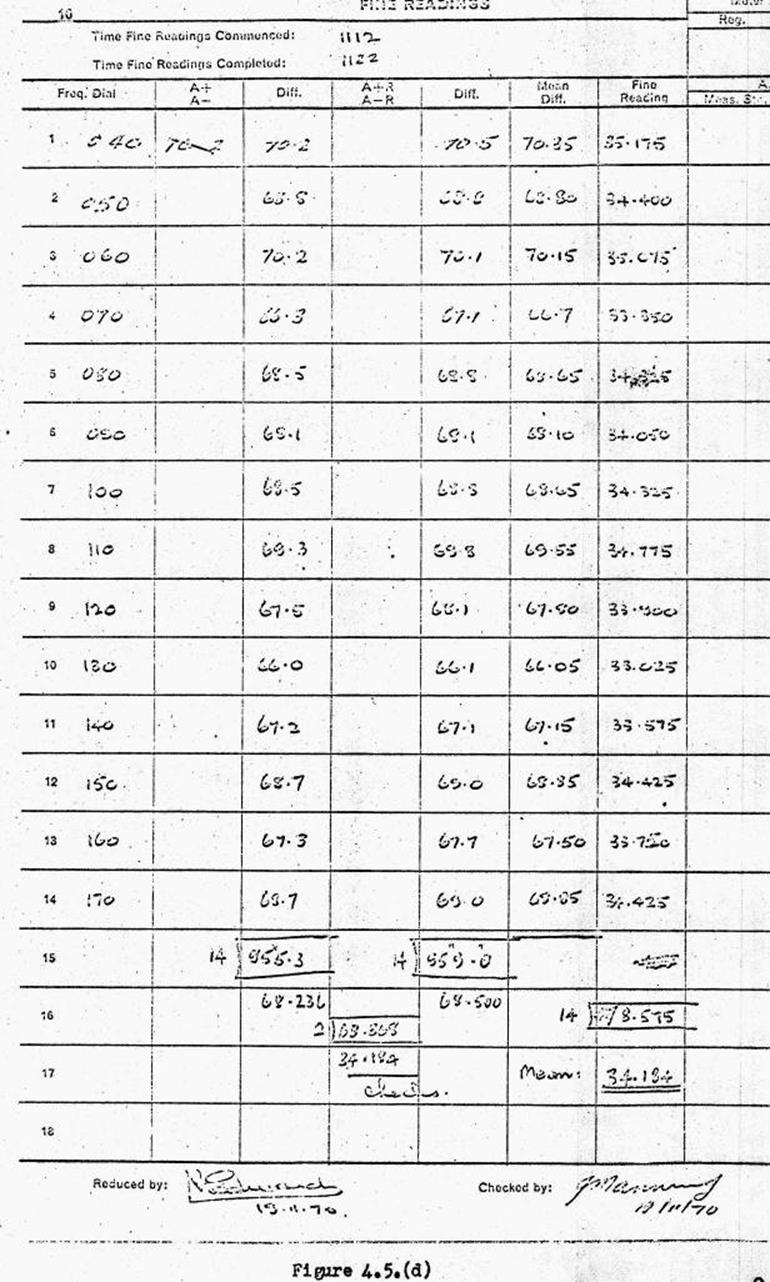

4.6.
TELLUROMETER,
MRA-4 – MANUAL
The
manual is in PDF format.
5 The Compass
5.1.1 It is often desirable in
field surveying
to obtain
relative directions to other points, or to find these points from given
directions. Where great precision is not required, a convenient means of doing
this is afforded by the “Magnetic Compass”.
This instrument has been
in use in various forms and stages of refinement for many hundreds of years. In
the most primitive form, the compass probably consisted of a piece of thread suspending
a piece of natural magnetic ore.
At some later date, it was
found that pieces of steel could be magnetised in various ways, so needles were
made which could be pivoted over a divided card. Beginning with quadrants named
for the prevailing winds, the card was sub-divided progressively into more and
more directions, each with a specific name derived from the cardinal points,
until the consequent complexity of tees system forced a change to the present
method of dividing the circle into 360°
numbered clockwise.
5.1.2 The
Prismatic Compass
This is the normal instrument used within the Division, it consists of a thin
magnetised bar, mounted on a pivot in the centre of a circular box. On the
magnetised bar is mounted a circular card which is graduated in degrees with
zero coinciding with the southern end of the bar.
The main features of this
instrument are:-
(a)
It is
1½² to 2" in diameter and is hand held.
(b)
The
graduations are either on a card or on a light aluminium angular ring fastened
to the magnetised bar; the graduations therefore stay stationary with the bar, and the index turns with
the sighting vanes.
(c)
Readings
are taken through a magnifying prism, attached to the outer case, and the prism
reflects the magnified image of the graduations in a horizontal direction.
(d)
Readings
are taken with reference to the lower part of a wire in the front sighting
vane, as index.
(e)
The
prismatic attachment consists of a 45° reflecting prism with the
eye and reading faces made slightly convex so as to magnify the image of the graduations,
The prism can be moved up or down, on slides attached to the outside of the
case to provide adjustment for focusing the figures on the scale.
(f)
Modern prismatic compasses
are the liquid type. This simply means that the magnetised bar and its accompanying
disk float in a special fluid contained in the case. The aim of this
arrangement is to reduce wear of the pivot, and the bearing
on the bar. It also helps to steady the magnetised bar.
(g)
The
most prolific source of error in
compass work is misreading the scale, due entirely to the construction of the
instrument and of the prism method of reading. As viewed in the prism, the
numbered graduations increase to the left instead of the right as expected.
Although the card is divided to single degrees, only every tenth is figured, so
it is essential to establish between which two “tens” the bearing lies. This
gives the correct “sense” in which to read the scale. For example, "62" is
commonly misread as “58”. By "bracketing" the bearing, saving
mentally" it lies between “60” and “70”; read “62”, no such mistake can
occur.

Figure
5.1.2. Prismatic Compass
5.1.3 Magnetic
Declination
Earth’s magnetic field originated from electric currents in its molten core, and can be likened to a short very strong bar magnet
at the centre, pointing 11°
from the axis of rotation.
This means that Magnetic North, although generally close True
North “declines" from it over the Earth's surface, by varying amounts which can be
found, and are called the "magnetic declination" of' that place.
Magnetic bearings can thus be related to True North.
Because this relationship is not absolutely constant and because
of other variations in the magnetic field, and also in compass manufacture, it
will be found that different compasses seldom give the same bearing for a line.
However, even in the presence of strong local attraction, all compasses will read angles
between points with reasonable accuracy. In fact, "compass
theodolites" using this principle, are manufactured today, so where possible this
approach should
be used.
5.1.4 Compass
error
If magnetic bearings are required, it is sound practise to calibrate the compass to
establish its "compass
error" each time it is shifted to a new locality. This used to be a tedious task in
un-mapped areas, but is a simple matter now that reliable maps are available
for all of Australia. By comparing a compass bearing with the true bearing of an identified line as protracted
from the map,
or, if between trig stations, obtaining the true bearing from the station summary, a
difference can be established.
If there is no real attraction, this difference should be the same
as the declination of the place ascertained from notes on the margin of the
map. If it is not, the disagreement is the compass error of that particular
compass and should be noted. In any case the difference would include the error due to local attraction and is the amount to be
applied at that particular station.
If marked on the compass case, it should be written on in pencil so that it
can be altered when a change is found at a subsequent comparison, in a new
area.
It is suggested that the notation be in the form "reads 2° low” rather than “-2°" which can be confusing.
As mentioned before, the compass error contains the error for the effects of the “Local Field", which
will vary according to the geology of the area. Over that part of Australia
where sedimentary rock predominates, it can be taken as a rough guide, that
errors of more than 10 minutes will occur at 10% of locations.
5.1.5 Protracting
bearings from a map
Where approximate bearings are required from a map, i.e. the
1:250,000 series,
the grid
lines, rather than
the faint Latitude
and Longitude graticules, are the most convenient from which to protract the
bearings. This does introduce a small error, if the map sheet happens to be
close to the Map Zone boundary. However, taking into account the general
accuracy of the compass, it would only in rare cases be worthwhile to rule true
meridians from the Longitude graticules, from which to protract bearings.
To obtain the magnetic bearing of a line, from the map, the true
bearing is protracted, then the magnetic declination added or subtracted from
that true bearing, to give the magnetic bearing.
When declination is East:-
Subtract from true bearing.
When declination is West:-
Add to true bearing.
Example:- True
bearing 265°
Declination East
- 5°
Magnetic nearing 260°
To obtain the true bearing
from the magnetic bearing, the rule is reversed:-
When declination is East:- Add to magnetic
bearing.
When declination is West:-
Subtract from magnetic bearing.
Probably the best way of obtaining magnetic bearing from a map is
to set the protractor so that it is oriented with 0° along the line to magnetic North. Proceed as follows:‑
(a)
Set
centre mark of the
protractor over the point from which bearings are to be read. Orient to true north by keeping parallel to the grid
lines.
(b)
Then
mark with pencil the angle of declination as shown on the map margin, i.e.
declination 5° East,
mark 5° to
the east of North.
(c)
Turn
north point
of protractor to coincide with the 5° mark.
(d)
Magnetic
bearings can now be read directly from the map.
6 Mirrors and Heliographs
6.1 Mirrors
When normal opaque targets, such as beacons or cairns cannot be
seen clearly in daylight, either because of atmospheric haze or excessive
distance, other
means mast be used to make them visible. One such alternative is a strong electric lamp, but this requires
a heavy lead acid battery to supply the power. In cloud free areas, however, a good signal can be
improvised from a small hand mirror, using it to reflect the sun's rays to the
desired station. This is suitable only in those cases where accurate plumbing
of the light is not required, and is mainly used for proving intervisibility of points. Another
use for the hand held mirror is to direct a helicopter pilot to your position
in country which lacks detail.
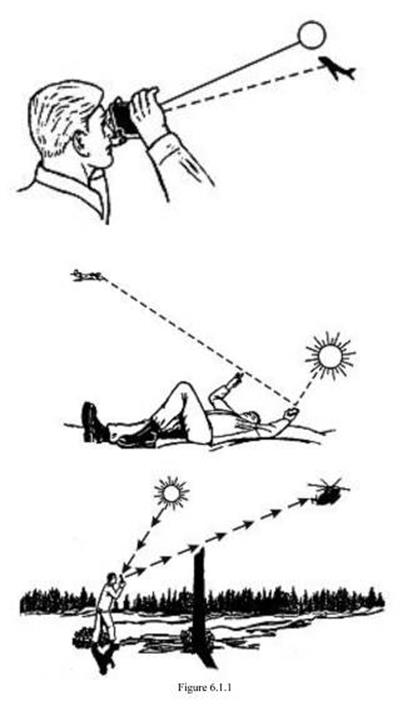
Any plane mirror of about six inches diameter, is suitable, and,
for convenience, can be provided with a small central “peephole” from which the
silvering has been removed. Using this mirror, it is possible to reflect the
sun's rays in
most directions and by adding a second mirror, to reflect a beam directly away from the sun.
By looking through the peephole, held close to the eye and aligning a small
stick, or the thumbnail, at arm's
length with the distant station, it is possible to shine a beam to it by
centring the shadow of the peephole on the tip of the stick or thumbnail. See Figure
6.1.1.
6.1.2 The
Heliograph
For observations requiring a precisely centred beam for extended
periods of time, a more elaborate mirror instrument is employed. It is the
military “Helio 5 inch Mk V”, a heliograph designed originally for signalling
purposes. It uses one or two mirrors as required, and has an associated
sighting system. See Figures 6.1.2(a) and 6.1.2(b).
It consists essentially or a
circular mirror mounted on a portable tripod, in such a way that it can be rotated in both horizontal and vertical
planes, about its centre, which is marked by a “dot”, a non-reflecting area about one eighth of an inch in diameter. This forms a dark. Spot in the centre of the reflected beam of light. A “radial arm” carries a foresight, or sometimes another mirror, to beam
the sun’s rays in
any predetermined direction.
In general, the single or “simplex” mirror set up is suitable for beaming in all
directions in the semi-circle towards the sun, while the two mirror or “duplex” set up is required for the sector away from the sun. The beam from the helio is a cone with a
spread of about fifty feet per mile of distance, and looks at long range, similar
to a very bright
star. It has been observed at more than fifty-five miles in Australia, which agrees with the rough criterion of one inch of mirror for every ten miles of
distance covered.
6.1.3 Setting
up the Helio
Decide whether one or two mirrors are necessary. This depends on
the relative directions of the sun and of the distant station i.e. on the angle
between them. If this angle is less than 120°, measured left or right from the sun, it is more convenient to
use the simplex or single mirror set up, even though at 120° the effective aperture is reduced by half, and the range is thus
restricted to about 25 miles. If this is acceptable the duplex or two mirror set up need
only be used for the remaining 120°
sector. It can, however, cover much more than this.
6.1.4 Simplex
helio
(a)
Assemble
helio as in Figure 6.1.2(a), and plumb the tripod over the ground mark, making
sure the radial arm is level by viewing it in two directions against the
horizon.
(b)
Direct
the radial arm and jointed sighting vane towards the distant station.
(c)
Rotate
the mirror, by means of the horizontal adjustment screw to point midway between
the sun and the distant station then tilt it with the vertical adjustment
screw, so that the “dot” in the centre of the beam is brought to the centre of
the cross of the foresight. This completes the approximate set up, and places
the instrument in a convenient state for precise alignment.
(d)
With
the back of the head to the sun, look into the mirror and line up the eye with
the central dot and the cross of the foresight. Locate the image of the distant
station in the mirror and move the foresight until it lines on the distant station and the
centre dot of the mirror. Moving the mirror will not alter the line of sight,
and will achieve only a shift of the head. For very long lines the final
alignment is best checked with the eye at least three feet from the mirror. Centre
the shadow of the dot, which defines the centre of the reflected beam, on that
part of the enamelled flap which coincides with the cross of the foresight.
(e)
This
completes the accurate alignment which will remain only until the dot moves off
centre. As the sun moves, it will be necessary to continually readjust the
mirror within every two minutes.
6.1.5 Duplex
Helio
(a)
Assemble
helio as in Figure 6.1.2(b), and facing the sun, set the duplex mirror end of
the radial arm to point 45° off the sun and on the
same side of it as the distant station.
(b)
Move
the instrument bodilv without rotation, to a position where the duplex mirror
can be plumbed over the station mark. DO NOT PLUMB THE TRIPOD CENTRE OVER THE
MARK. In the duplex set up, the distant station receives the beam from the
duplex mirror which is facing that station, not the simplex mirror which faces the sun.
(c)
Adjust the simplex mirror, by means of the horizontal and vertical adjustment screws, so that
the dot is reflected to the central mark of the Duplex mirror.
(d)
Face the
Duplex mirror towards the distant station then point it midway between the
distant station and the simplex mirror. Now stand behind the Duplex mirror, in
line with the distant station, and looking towards it, check that the simplex
mirror is not in the way.
If it is, move the radial
arm to provide clearance. This movement shifts the Duplex mirror off the
station mark, so the whole instrument will have to be moved again, bodily and
without rotation, to replumb the Duplex mirror; repeat the alignment procedure.
This completes the approximate set up and places the instrument in a convenient
state for precise alignment.
(e) With the back of the head
to the sun, look into the simplex mirror and line up the eye with the central
spots of the two mirrors. Locate the image of the distant station in the mirror
and bring it into line with the two central spots by manipulating the Duplex
mirror. As before, the final alignment is best checked with the eye at least
three feet from the mirror.
(f) Using the horizontal and
vertical adjustment screws bring the dot to the central mark of the Duplex
mirror. This completes the accurate alignment, which will remain so only until
the dot moves off centre. As before, the mirror must be readjusted within two
minutes.
It is important to keep
the mirrors clean and see that all controls are oiled and move freely. Any
looseness in the head of the tripod or in the pivots or screws of the helio
will cause vibration of the instrument by the wind. This in turn, prevents the
distant station receiving a steady beam, or possibly any beam at all.
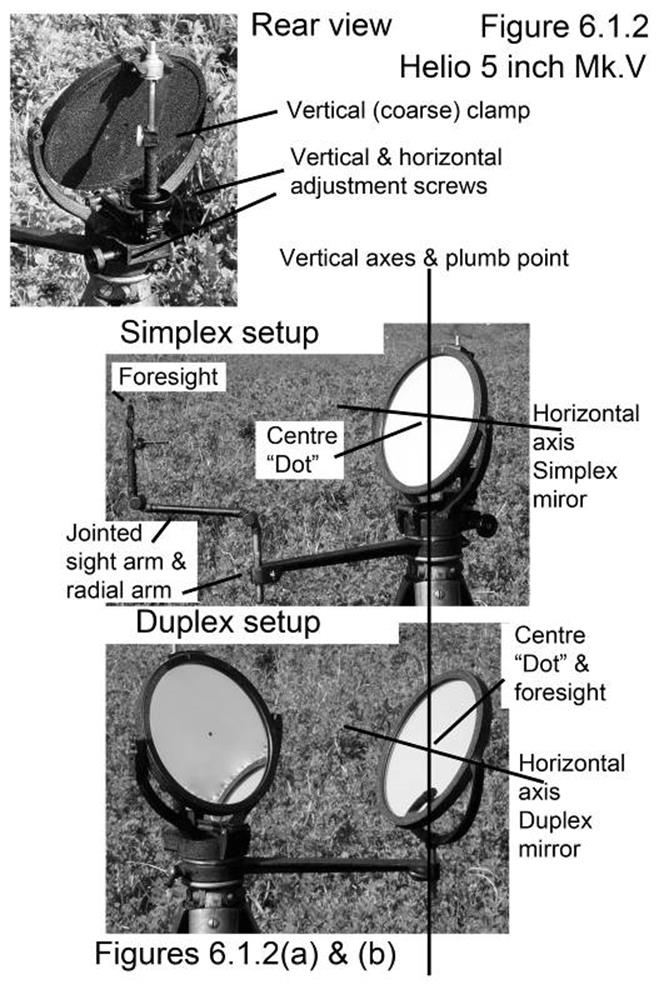
7. Station Marks and Marking
7.1.1
The
station mark
This is the mark at each
station, to which all coordinates, observations, and measurements are related
even though the actual observations or measurements may not have been made, to or
from that exact point. Over the years, these marks have been established by a
number of authorities, thus there is a wide difference in the types of marks
used. Mainly, the mark is a brass plaque about 77mm (3") in diameter, or a
13mm (½²) diameter copper tube, brass or stool rod, set in a concrete block. The brass plaque usually bears
the name of the authority establishing the station, and often has the station
name or number stamped on the surface.
Some authorities, for
security often have a sub-surface mark set directly below the station mark. This is not always possible,
particularly on rocky hills, however it is a wise precaution wherever possible.
Figure 7.1.1(a) shows the
type of mark recently used by the Division. The GI pipe to anchor the pole type
beacon protrudes about 38mm (1.5²)
above the concrete block. If no beacon is to be erected, the GI pipe is
dispensed with, and the 13mm (½²) copper tube used instead with its top flush with the top of the
concrete block. The station number is moulded into the concrete block which is
painted white, with the letters picked out in black.
Details of the above marks
are supplied for information only, to help identify marks when visiting
stations previously established.
Type of Station Mark
previously used :
Surface mark:-
1½² diameter GI pipe (beacon anchor) with ½² diameter copper tube cemented in centre. If no beacon to be
erected use only copper tube.
Figure 7.1.1(a)
Sub-surface mark:-
½² diameter copper tube cemented in centre of concrete block.
In most cases only the
surface mark was emplaced.
The type of station mark laid down in the ''Specifications for
Ground Control Surveys" will now be used at all times. Details are as
follows:-
Station mark for one
degree or half degree mapping control stations.
(a)
The
monumentation of the station shall conform, with due regard to ground surface
conditions, to the specifications illustrated, guard posts shall be of in
concrete to a depth of at least 0.4 metres, and painted in alternate bands of
red and white enamel, 0.25m wide.
(b)
Every
effort shall be made to use good quality screened angulated gravel and sand. In
certain areas, it may be found necessary to carry a supply of these materials.
(c)
After making use of the station mark mould, the concrete structure should be neatly
trowelled off, and should provide a smooth surface to conform with the shape
illustrated in Figure 7.1.1(c). At this stage, while the concrete is still
soft, dies of the appropriate letters and, numbers for the station should be pressed into the surface. These
dies are removed as soon as the surface is firm enough. The surface should be
trowelled to a hard finish.
(d)
When
the surface is partially dry “Boncote" ( a preparation for whitening and
coating concrete surfaces) should be painted on the structure with a fexible
paint brush. The impressed letters and numbers are picked cut with black paint.
If time permits, a second coat of gloss paint makes all the difference to the white station mark.
(e)
A
circular trench four metres in diameter, 0.3m wide and 0.3m deep with vertical
sides should be dug with the station mark as the centre for subsequent aerial
photography. Where ground conditions prevent the digging of a well defined
trench, a circle of white painted stones, four metres in diameter should be
built to provide a suitable target for aerial photography. See Figure 7.1.1(e).
(f)
All
intermediate stations required
to interconnect the one degree and one half degree stations should be marked
with the standard station mark described, but only one guard post is emplanted
as a witness post. No circular trench is required.
(g)
If it is necessary to place a
station on a sandridge, or on ground
subject to erosion, the station mark should consist of lengths of 0.02 to 0.05
metres internal diameter galvanised iron water pipe, each preferably 1.5 metres
long, Sufficient lengths should be coupled together and driven to refusal, so
that about 0.3m of the pipe shall protrude vertically above the general surface
of the ground. The number of this station should be stamped on a tag of flat
galvanised iron or aluminium sheet, 0.1 metres by 0.18 metres, and not less
than 1mm thick. The tag should be firmly attached by wire to the pipe. Any suitable nearby trees should be blazed and
the number of the station should be chiselled on the blaze. The trees should be
referenced by bearing and distance from the station mark to the blaze.
Measurements should be to a galvanised
roofing nail, fully driven centrally in the blaze.
(h)
Where,
a station of the type described in (g) is estalished, an additional satellite station will be established, which shall:-
§
Have a
unique number, not a consecutive
number, with that of the station on the sandridge.
·
Be constructed in conformity
with the standard station mark, in every way.
·
Be in
a safe and permanent position; in sandridge country, on the nearest firm
ground; such as the flat area between sandridges usually about 200 metres from the station on the sandridge.
·
Be
connected to the sandridge station through a well-proportioned triangle, the third
point being placed
on the firm ground as a reference mark. All sides and angles of the triangle to be measured and also referred to the
traverse azimuth.
7.1.2
Reference
Marks
These are the marks at each station, which are placed so that the station
mark can be replaced, in its exact position
if it has been
removed or damaged. At existing stations, various types of marks have been placed, i.e. brass
plaques, copper tubes, steel rods, etc in concrete blocks.
The type of reference mark
laid down in
the ''Specifications for Ground Control Surveys" will now be used at all
times:-
(a) Reference marks shall be
three steel star pickets, (fence droppers) each of approximately 1.5m in
length, driven flush with the ground, or to refusal, and cut off flush with the
ground.
The picket should be
surrounded with a collar of concrete 20cms in diameter, and not less than 15cms
deep, with the upper surface flush with the top of the picket. The tops of the
pickets should be centre-punched for exact reference measurements. Normally two
of the pickets should be placed exactly on line to each of the adjacent
stations, the third being located at a convenient point to provide maximum
advantage for the recovery of the station.
Reference marks should, where
possible, be placed in positions where they are least likely to be disturbed;
for example under fences, and generally about 6 metres from the station. Any
permanent structures (bore casings, concrete bridges, large concrete culverts,
etc) should be accurately connected to the traverse station. Also connections
of reasonable distance (up to 500 metres) should be made to corner fence posts
and distinct angles in fence lines.

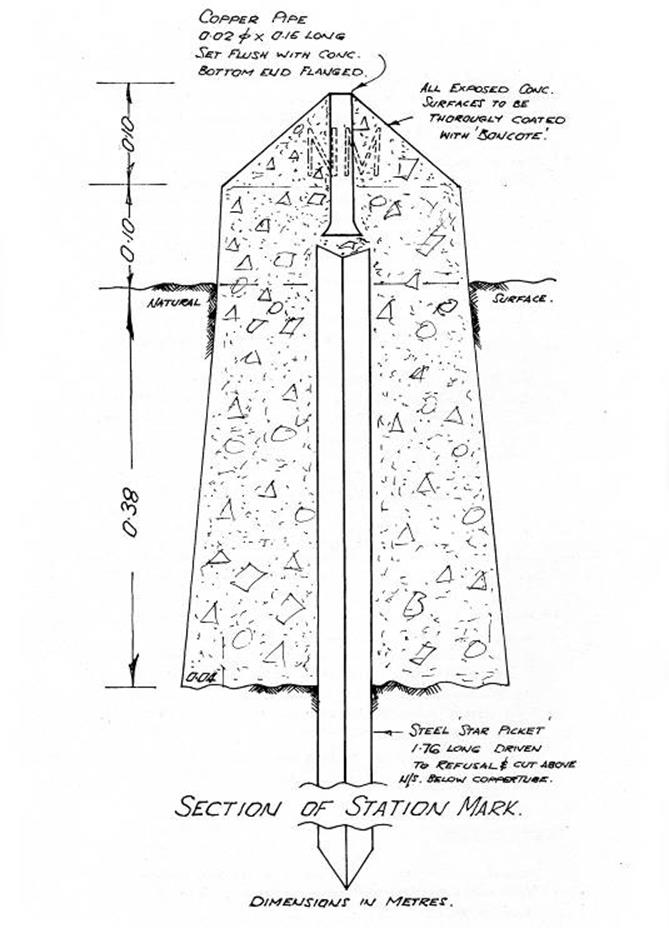
Figure
7.1.1(c). Station Mark at present in use
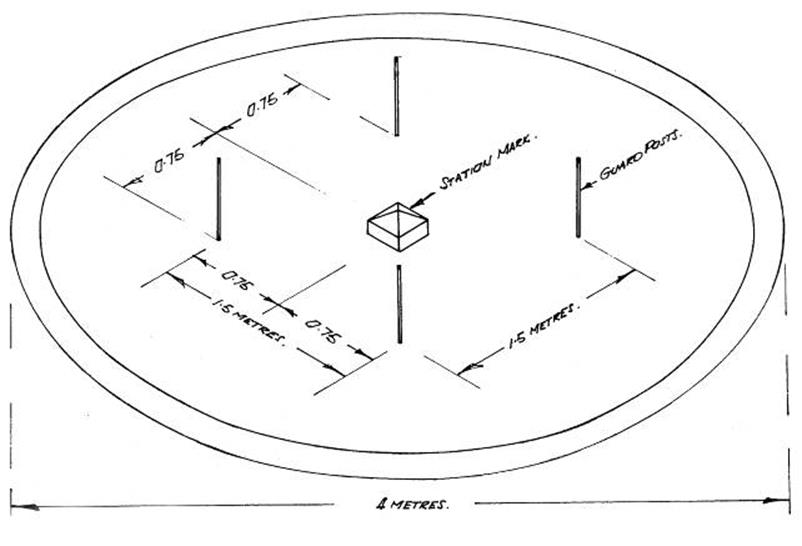
Figure
7.1.1(e)
Sketch of
Station Layout – Figure 7.1.1(e)
Guard posts are 0.06m x 1.06m long and of GI pipe with “cap” on top. They are
to be set in concrete, painted white with red bands 0.25m wide. The posts are
placed in a square to the dimensions shown below. The sides of the square form
are to be oriented north-south, east-west.
A circular
trench 4m in diameter, 0.3m wide and 0.3m deep to be dug for photo
identification purposes. It is important for the trench to be concentric with
the station mark.
7.2 Types
of Marks which have been in general use
Details of these marks are given for general interest, as they
will be encountered when visiting established stations in the course of normal
field duties.
Also, at some stage, it might be necessary to erect a rock cairn
or beacon, or lay out a base line to establish a recovery mark very accurately.
In this event, the following notes should be most useful.
7.2.1 Witness
Posts
While these could be of value at all stations, they are usually
placed only at stations where no large cairn, beacon or tower, which can easily
be seen, has been erected. The post is either about 50mm diameter GI pipe, or
75mm square timber. It is usually painted white with the name or number of the station in black. The
post would be about 1.2 metres long with about 0.6 metres out of the ground. A
measurement is taken from the station mark to the base of the post, and a
direction from the RO, is observed.
7.2.2 Reference
trees
In timbered country, a shield is often cut in a large, solid, tree
and the station number cut with a chisel in the shield. If the shield is then
painted a bright red, with the station number picked out in yellow, a very good
"witness post" and "reference mark" which will last for many years, has been
established.
7.2.3 Recovery
mark at First Order stations established on a sandridge
To be read in conjunction
with 3.5.3.
The term Recovery Mark and Reference Mark are often, and probably quite correctly, taken to mean the same thing. However, within the Division, it has come to
be accepted that those marks close to the station are Reference Marks, and those marks
set on firm
ground some distance away, are Recovery
Marks. The establishment of the First Order Recovery Mark involves quite a lot
of work, normally
4 men for
about 2 days, and needs additional equipment to that which is usually carried.
The following method was employed to establish First Order
Recovery Marks:-
(a)
A
point was selected on firm ground about 200 metres from or as close as possible to
the station mark.
(b)
A temporary
mark was made, the theodolite set over it, and two base lines just over 200
yards long, at right angles to the line Recovery Mark-Station Mark were marked
out.
(c)
This
line was cleared either by hand or by dragging a “scraper” behind a vehicle.
(d)
When the line had been fairly well
cleared, the Recovery Mark was set in. Usually a post-hole digger was used to make a hole about 2½¢ deep. The top 1½¢ was cut square with a
narrow shovel, and a 5¢ by 1½² diameter G.I. pipe was driven to within about 2² of
ground level. The hole was filled with concrete to ground level, and the
station number,
with the letters RM, was moulded into the concrete.
The pipe was filled with earth, and a ½² diameter copper tube was set in cement in the top of the G.I. pipe.
(e)
Set a
theodolite over this mark. An angle of exactly 90° was turned from the station
mark. An exact
300' plus 1² was laid out along this
line, and a 5¢ steel picket was driven
in this position to within about 3" of ground level. If unable to drive
right in, or if the top of post is damaged, cut off with a hacksaw 3" above ground level. Mark point on top of post with centre punch, at exactly 90° from
station mark.
(f)
Turn
theodolite to exactly 270°
from station mark. Repeat everything mentioned in (e).
(g)
Carefully,
by hand
shovelling, clear all twigs, bumps, etc, between each base terminal, and the
recovery mark. When this is done, the recovery mark and base lines are ready for measurement and
angular work.
(h)
The
idea is, by reading all horizontal and vertical angles, and very carefully measuring the two base lines, the
distance RM-Station Mark can be calculated twice, also that with all three
marks, or any one of them, the station mark can be re-located, if lost because
of erosion.
(i)
A
circular trench 12¢ in diameter, 18² deep and 18'' wide was dug around the Recovery Mark. The spoil
was piled around
the outside of the trench, and if the mound is not large enough a further small trench was dug outside the mound, the spoil being added to the mound.
(j)
A bush tripod of three
"Y" shaped trunks about 8¢
long was erected over the recovery mark. The bark was stripped from trunks, and
they were well painted with primer and two coats of white paint before
erection. The station
number is painted on one of the
trunks.
It is not likely that such elaborate marks will be established in
the future, however the general technique may be used for a base line to connect a recovery mark to the
traverse station.
7.2.4 Rock
Cairns
Many
of the Division’s stations have been marked with a pole and vanes inside a large rock
cairn. Four experienced persons can assemble and erect the beacon and build an 8¢ (about 2.7m.) diameter by 6¢ (about 2m) high cairn in
about half a day, as long as there is plenty of rock available right at the
site. A crowbar is necessary to
lever the rock free. The following routine should be adopted:
(a)
Assemble
the beacon; put in the station mark.
(b)
Gather
plenty of rock
of all sizes, leave it in a circle around but well clear of the station mark.
(c)
Mark
an 8' (2.7m) circle around the station mark and lay the base rocks with their outer edge just touching
this line. Take care to "seat" them firmly; do not lay any long,
narrow rocks around the circle as they will
be unstable. These should be laid with the narrow end towards the station mark.
See figure 7.2.4(a).
(d)
Build
a second layer of rocks overlapping the vertical joins as a bricklayer does. See
Figure 7.2.4(b).
(e)
Stand
up the beacon, staying it with the steel bars provided, plumb with a builder’s level, and tighten the
bolts holding the steel stay bars. See Figure 7.2.4(b).
(f)
Fill
the interior with
small and
medium sized rocks to the approximate height of the wall.
(g)
Build
the wall another two layers higher, fill in the interior, as before. The wall should taper in, slightly. A
stick with various marks, should be continuously used as a gauge to keep the
cairn circular, and the pole central. Stand back and "eye off” the shape
of the cairn to see it is symmetrical. Again plumb the beacon with the builder’s level, and straighten
pole, if necessary. After this it will be impossible to alter the angle of the pole, without dismantling the cairn.
(h)
Continue
in a like manner until the cairn is nearly completed. The top section needs only smaller rocks, piled as
shown in Figure 7.2.4(c). This should be done without spoiling the symmetry of the cairn.
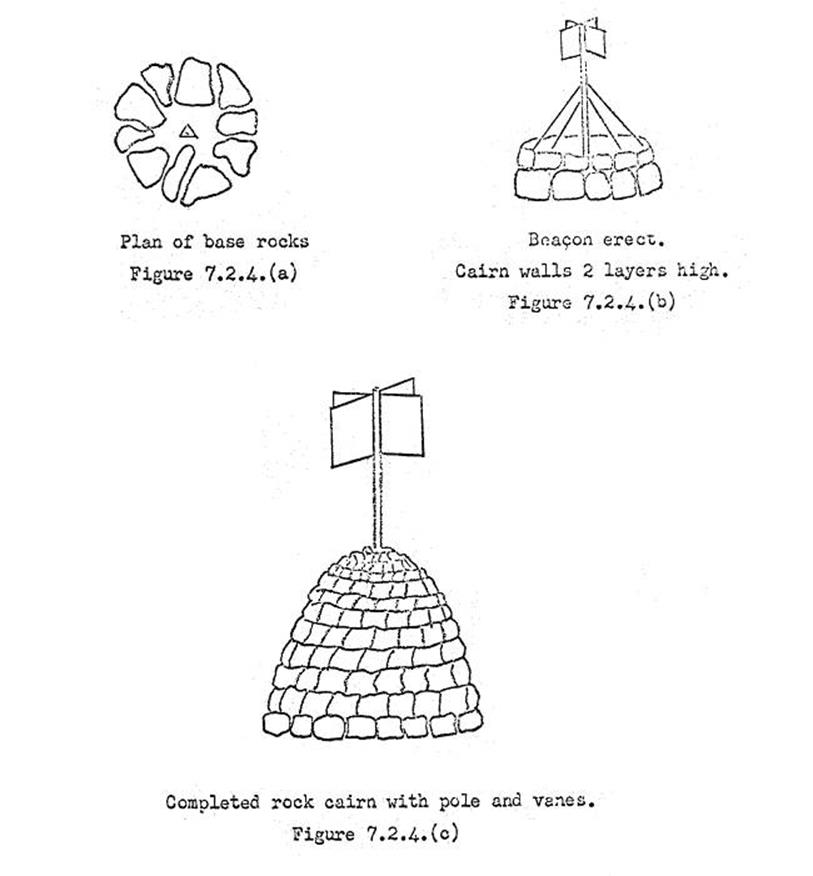
7.2.5 Beacons,
Quadripod and Tripod
Some stations have a quadripod or tripod type beacon with vanes,
erected over the station mark. The height to the top of the mast is about 15 to
20 feet (5-7 metres approximately).
Where these beacons exist it is possible to do the observations
and measurements directly from the station mark. However, the vanes, if being
observed from the distant stations, must be checked to see that they are
directly above the station mark. See Figure 3.7.2 – Plumbing beacons.
The erection of these beacons is fairly straight forward; plans of
the exact beacon use, would be required for assembly and the positioning of the
anchor points.
All exposed station marks should, where possible, be covered with a small cairns of rocks.
Reference marks should not be too obvious in case of vandalism; any authorised
person will soon locate them when equipped with a station summary and measuring
tape.
As stations have been established by various authorities, the type of station marking, types of reference marks,
and even units of measurement, will vary considerably throughout Australia. Measurements may be in feet and inches, feet and decimals of a foot,
links, or metres.
8. Erection of Towers and Mills Scaffolding Observing Platforms
Observing towers with Mills scaffolding observing platforms have
been necessary in the past, and no doubt, may have to be resorted to for
certain types of terrain, in the future.
The towers used have been 20 or 30 feet (6.096 or 9.144m) tripod
type, windmill towers, with special adjustable "feet" to accurately
plumb the tower "head", which takes the instruments, over the station
mark.
8.1.1 Stand
point for the Tower
The observing towers are set on, and bolted to, concrete blocks
about 0.3m by 0.3m by 0.45m deep. Dimensions for positioning these blocks and bolts relative to the station
mark are shown in Figure 8.1.1(a).
A level or theodolite should be used to ensure that these blocks
are on the same plane, so that the tower head will be central above the station
mark. If many towers are to be erected a template
can easily be
devised to position
the blocks quickly and accurately. Blocks are usually reinforced with one or
two 0.45m steel posts driven into the bottom of the hole. At least 24 hours
drying is required before the tower can be bolted down.
8.1.2 Assembling
the Tower
No specialised knowledge is required to assemble these towers, but
it is essential to have a copy of Plan 515S, until the party becomes familiar
with the task. Figure 8.1.2(a) lists the parts in a tower. It is listed in 10'
(3.048m) bundles, as the towers are delivered.
Method of assembly:-
(a)
With
the base of the tower somewhere near the station mark lay the parts of the
tower on the ground, as it will go together.
(b)
Assemble
one side of the tower, flat on the ground without tightening the bolts.
(c)
Assemble
the other two side of the tower, working from the top downwards. It may be
necessary to "shake" the tower so that the bolts their respective
holes. A round file is handy to clear, or enlarge, some bolt holes.
When the tower is assembled add footplates and tighten down all
bolts. The bolts holding the footplates should be so positioned in their slots
that the same amount of adjustment, up or down, is available.
8.1.3 Erecting
the Tower
Four strong men can erect a thirty foot tower, if two of the feet are
securely anchored to prevent slipping.
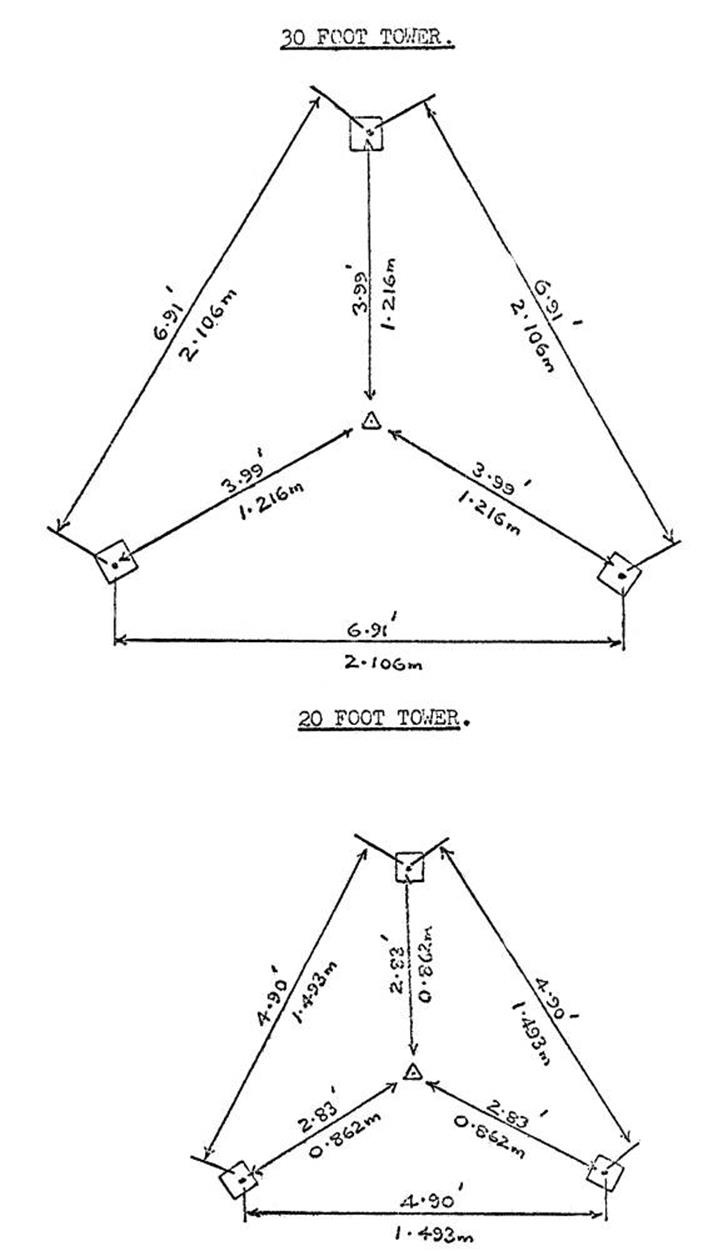
Figure
8.1.1(a)
|
30 FOOT
(9.144m) OBSERVING TOWERS
|
|
Bundle number 1:- (top 10 feet, 3.048m, or 10 ft tower)
|
|
Main angle
|
Length 10 feet
|
3
|
|
Girts
|
10ft 11 7/16²
|
3
|
|
Girts
|
10ft 23 15/16"
|
3
|
|
Braces
|
5 ft 2 13/16"
|
6
|
|
Top ties
|
5 ft 4"
|
3
|
|
Bundle number 2:- (Second 10 ft. 1 & 2 make 20 ft tower,
6.148m.)
|
|
Main angle
|
Length 10 feet
|
3
|
|
Girts
|
2 ft 11 7/16"
|
3
|
|
Girts
|
3 ft 11 15/16"
|
3
|
|
Braces
|
5 ft 2 7/16"
|
6
|
|
Braces
|
6 ft 0 7/8"
|
6
|
|
Bundle number 3:- (Bottom 10 It 1,2 & 3 make 30 ft tower,
9.144m.)
|
|
Main angle
|
Length 10 feet
|
3
|
|
Girts
|
4 ft 11 7/16"
|
3
|
|
Girts
|
5 ft 11 15/16"
|
3
|
|
Braces
|
6 ft 4 9/16"
|
6
|
|
Braces
|
7 ft 4 11/16
|
6
|
|
Sundries:-
|
|
Tower feet
|
|
3
|
|
Bolts 1" x 3/8" UNC –HTS
|
|
12
|
|
Bolts ¾” x 3/8" BSW
|
|
21
|
|
Bolts 1" x 3/8" BSW
|
|
60
|
|
Bolts 6" x 5/8" BSW-HD
|
|
3
|
|
Washers standard 3/8"
|
|
72
|
|
Washers standard 5/8"
|
|
3
|
|
Weights:-
|
|
A twenty foot tower weighs 198lbs, and a thirty foot tower
weighs 308lbs. They take up little space, only three 10feet long compact
bundles per tower.
|
Figure
8.1.2(a)
Method:-
(a)
Move
the tower so that two of the feet are close to their concrete anchor bolts.
Securely tie each of these feet to a bolt, passing the rope through the hole in the footplate.
Lift the head of the tower and "walk" forward pushing it up.
(b)
Nearing
the half-way position, the weight begins to tell so one man runs to the tower
base and throws his weight on to the foot which is not resting on the ground,
thus helping to drag the tower upright. As the weight eases, he steadies the tower and gently lowers
the foot to the ground.
(c)
The
footplates are then lifted over each bolt, and the tower is firmly bolted down.
(d)
The
tower is
approximately plumbed as explained in 3.7.1. The final, accurate plumbing must wait until the erection of the
scaffolding and the attachment of the tower head.
8.2 Necessary
Tower Attachments
The tower head, upon which the theodolite or tellurometer is
mounted is carried in a separate box. Certain other attachments which are
necessary for tower observations are also required.
8.2.1 Tower
head
The former traversing tower head has been modified, and
simplified, so that the top plate only, is used. It fits directly on to the top
of the tower with three brackets; there is sufficient adjustment at the tower
feet, coupled with a small amount in the top brackets, to easily plumb the head
over the station mark. The new brackets give the single top plate much greater stability, thus the theodolite
is much easier to level, and will hold its level for longer periods. Figure 8.2.1(a)
gives an exploded view of the tower head and brackets, and is sufficiently clear to indicate the method of attachment.
8.2.2 Protection
of the Tower from sun and wind
Towers have to be protected from sun and wind during observations.
Hessian screens as shown in Figure 8.2.2(a) can be easily made if time permits.
If many towers are to be used, they definitely should be made. Where only a couple of, towers are to be occupied,
strips of hessian straight from the roll can be used. Ropes are attached by
gathering the hessian in a bunch; two strips of 6ft wide hessian are required
for each side, and usually it is sufficient to shield three sides at the most. An eight foot square of hessian or canvas
is required to roof the scaffolding. This is better than trying to bring the side strips over the top, to also
act as a roof.
8.2.3 Useful
attachments for Tower observations
(a)
If
lights are to be observed in the daylight, it is necessary at some angles of
light, i.e. when the sun shines
directly on the hessian, to have a black backing cloth behind the light, otherwise it disappears against the straw
coloured hessian. These strips of black cloth should be about 8 feet wide by 3 feet deep and matte black
not glossy.
(b)
Figure
8.2.3(b) shows a fitting to attach a Lucas light to the scaffolding, so that
the light can be shown from a position on line to the distant station.
(c)
Figure
8.2.3(c) shows an adaptor to attach a Lucas light to the theodolite position on
the tower head, so that a light can be shown from a position directly over the
station mark when that station is not occupied.
(d)
Figure
8.2.3(d) shows an adaptor to the above fittings for attachment of a
"flamethrower" type light (or helio for vertical angles only).
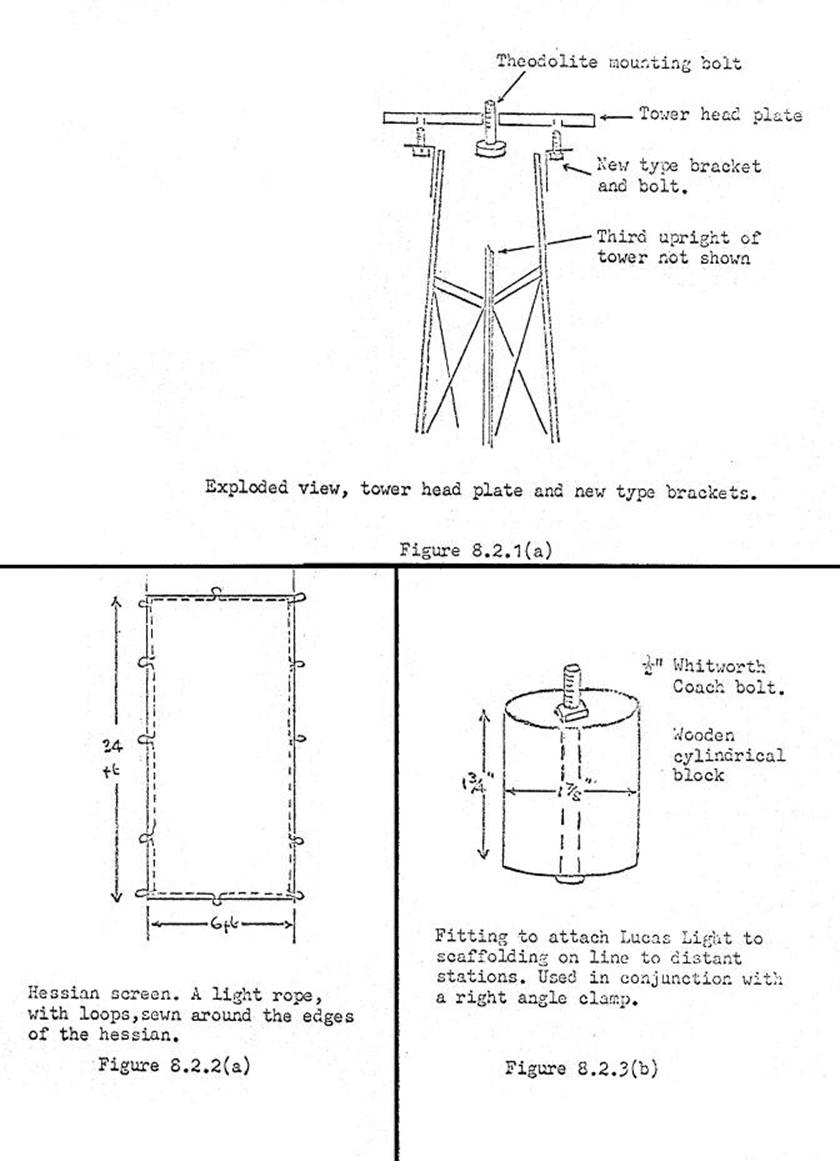
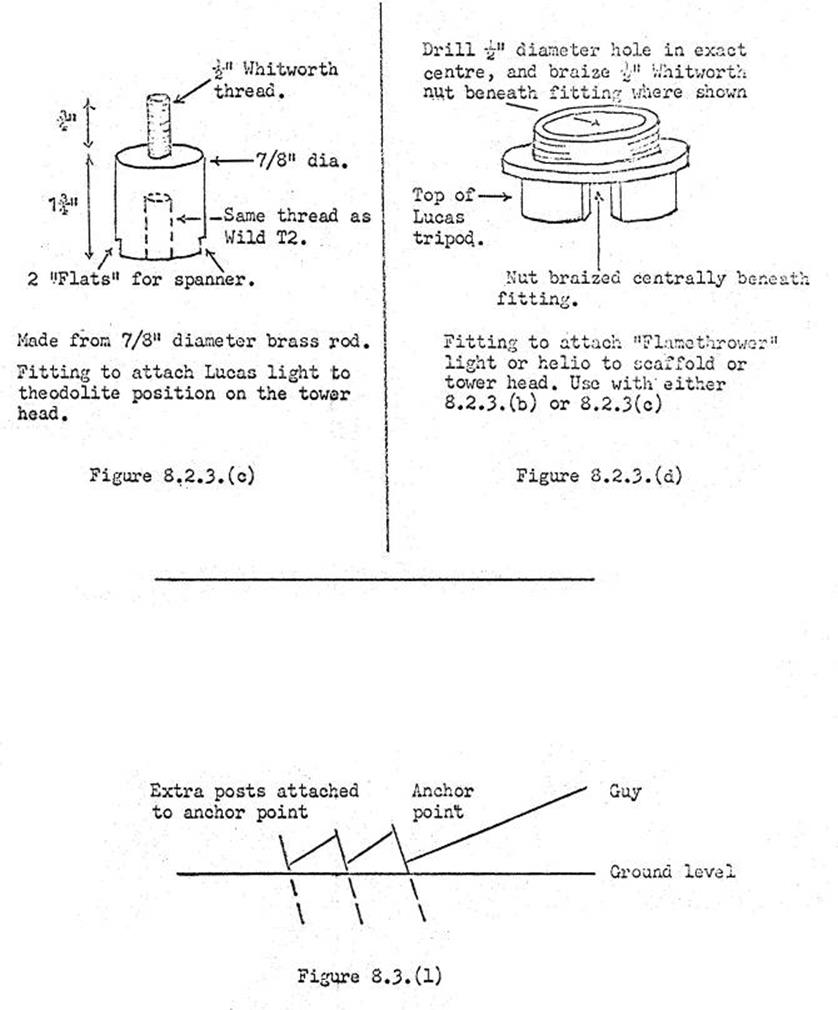
8.3. ERECTING A MILLS
SCAFFOLDING OBSERVING PLATFORM (30ft TOWER).
|
(a)
|
From
9 feet lengths of tube
make up 24 with right angle clamps
8 feet apart. This is done by
first constructing a "jig² from one 9 foot length and six very short lengths. These 22 lengths will now be called
standard horizontals.
(See
diagram "a" for sketch of "jig").
|
Figure “a”
|
|
(b)
|
Take
three 11 foot lengths (2 for uprights, 1 for a diagonal) and two standard horizontals. Form bottom side of the
scaffold as shown in "b1". From same amount of material form
"b2". Note that the diagonal is on the opposite slope. As these are
assembled on the ground, the standard horizontals are kept as far apart as
possible, while in all other stages of erection they can only be placed about
5 feet apart.
|
|
|
(c)
|
Mark a 1.724m (5.66ft) radius circle in the earth around the
station mark; level site, and roughly position the foot plates so that the
scaffolding will go up at right angles to the setting sun, and centrally over
the station mark. Keeping the scaffolding at right angles to the sun makes
for ease of shielding, later on.
|
|
|
(d)
|
Stand
“b1" and "b2" on opposite sides of the station mark, and join
with standard horizontals and diagonals. Note that all standard horizontals
and diagonals are on the outside. (See Figure "d”). At this stage position foot plates firmly
beneath each upright, and by standing back and using a plumbob, check that
the scaffolding is vertical. Adjust if necessary.
|
|
|
(e)
|
Although
the scaffolding can be erected without them, two planks are of great
assistance. Lay these on the top horizontals and stand four eleven foot
uprights in position. Continue erection for two more horizontal levels. As
previously mentioned, these are about 5 feet apart. (Chin height is a rough guide).
|
|
(f)
|
Five
men are the ideal team, one man at each upright and the other man to pass up
tubes as required. These are hung on the horizontals by resting the clamp on
that horizontal.
|
|
(g)
|
The
next horizontal level supports the platform, and its height is governed by
the height of the tower and the height of the observer. However, the whole,
platform can be adjusted, when complete, if within about 8 inches of its
correct position.
Two
standard horizontals are attached to the uprights, on the inside, this time. Four
horizontals(clamps slightly closer
8
feet) are laid across to support the bondwood platform. These are only
lightly clamped at this stage, as they will need adjusting to suit the
platform, later on. (See Figure 8.3).
|
|
(h)
|
The
last four diagonals take full advantage of the 11 foot tubes, by placing the
clamps almost at the extremities.
|
|
(i)
|
Two
standard horizontals are clamped on the inside, at waist height above
the platform, and two with clamps slightly closer are clamped across these
some eight inches in from the uprights. These form the girth rails, the idea
of bringing
two of
these rails eight inches inside the uprights is to cut down the space on the
observing platform, for safety reasons.
|
|
(j)
|
Four
standard horizontals are clamped just below the top inside of the
uprights. One 11 foot length (for gantry) and one 9 foot length are clamped
horizontally across the top to hold the canvas or hessian roof.
|
|
(k)
|
A
pulley is clamped on the gantry, bondwood platform hauled up, and laid on the
supports which are now adjusted to the holes in the platform. These supports are now clamped down firmly, and
the bondwood platform tied to these supports.
|
|
(l)
|
The
scaffolding must now be stayed with four guys. Right angle clamps are ideal
for attaching the guys to the 4 uprights.
The
guys at present in use are made from good quality steel cable with stainless
steel rigging screws for tensioning. Stainless steel fittings are also
provided for attaching the guys to the right angle clamps and to the steel
fence posts. The guys were made so that one can be attached to each twenty foot scaffold upright at
platform level. To gain the extra length required for a thirty foot scaffold,
two guys are joined together.
Five
foot steel fence posts are used as anchor points, and should be driven deeply
into the ground. Where there is any doubt about the hold of these posts in
the ground, an additional post or posts should be used to strengthen these
anchor points. See Figure 8.3(l). It must be remembered that when the
scaffold has the hessian screens attached, there is a tremendous strain on
the guys in even a moderate wind.
|
|
(m)
|
If
observations for azimuth on sigma Octantis are to be undertaken at least one of
the horizontal lengths forming the roof will have to be dispensed with, and
the gantry will have to be to the east or west and clear of the traverse
lines.
|
|
(n)
|
Requirements
for a thirty foot Mills scaffolding observing platform:-
|
|
Tubes.
11
foot:- 12 for uprights.
16
for
diagonals.
1 for gantry
9
foot:- (with right angle clamps 8'
apart)
16 below platform
2 at platform
2 at girth
4 at top
(with
right angle clamps a little less than 8' apart)
4 support
platform
2 at girth
1 at top
|
Sundries.
8
End to end couplers.
64 right angle clamps.
32
swivle clamps.
4
foot plates.
1
pulley with 70 ft of heavy rope.
8
guy wires with rigging screws and fittings.
4
steel fence
posts (at least).
|
|
(o)
|
Weight
of scaffolding
: Complete scaffolding for a thirty foot observing platform weighs about 1100 lbs. It is a bulky awkward
load to fit on a vehicle. Even when completely un-assembled, four thirty foot
scaffoldings leave little room to spare on a Bedford 5 ton truck. Where a long tower traverse is being undertaken, it is
essential to have two of these vehicles for shifting the scaffolding forward.
|
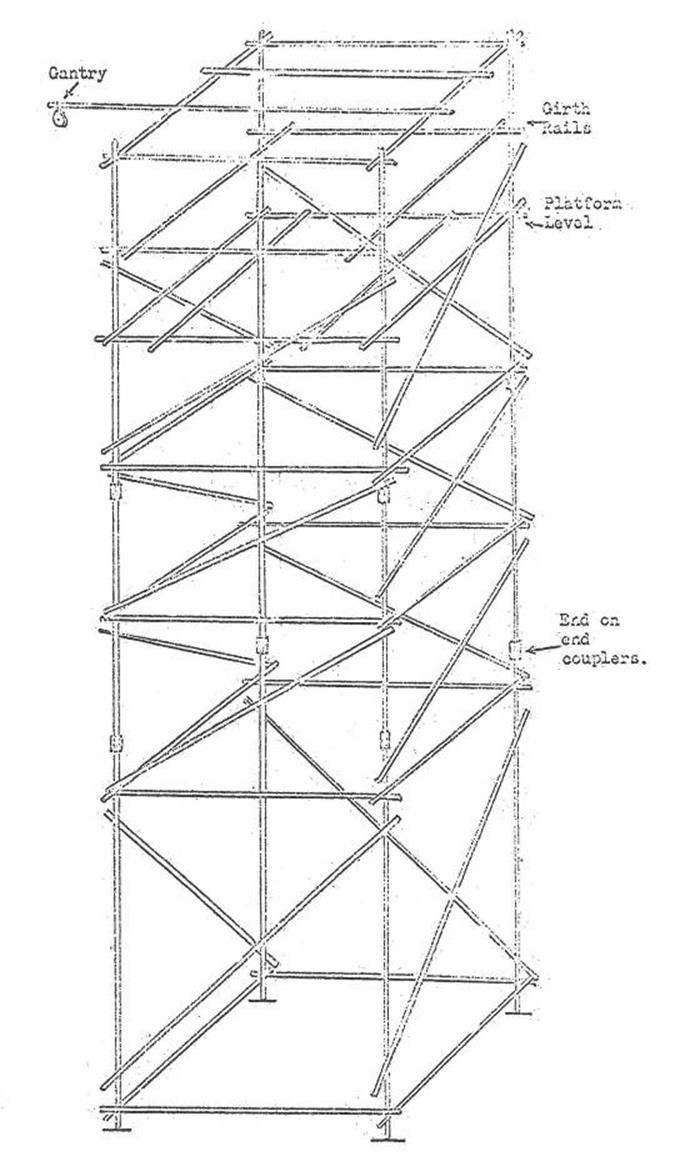
Figure
8.3. Observing Scaffolding (30 foot).
9. Access
Notes and Sketches
9.1 General
In order to enable a Mapping Control Station to be readily
revisited at a later date an access sketch is required to supplement the detail
shown on the map.
This sketch may vary from just a "cut out" of a section
of the map with the exact
location of the control point plotted, to a very detailed sketch necessary for
locating points in remote areas where mapping detail is scarce.
These sketches are usually compiled from speedo and compass
traverses supplemented with notes. These notes should be comprehensive so as to
avoid relying on the memory when drawing the sketch. Remember, some data from
the notes may be omitted if considered unnecessary on the sketch, but data from
the memory, which might not be completely accurate, if shown on the sketch may
mislead the user.
9.2 Field notes of the speedo
and compass traverse
Vehicle mileages to 1/10th mile and magnetic bearings are taken
along the route at road or track junctions, bends, creek crossings, gates,
fences, signposts, tanks dams, windmills, homesteads, airstrips and bridges
etc.
The start point for these mileages should be at an easily located
place such as a road junction, P.O., airstrip, homestead or bridge, etc.
Where access is difficult owing to poor tracks or featureless
country, piles of stones and blazed trees are helpful to mark the route,
particularly if time is taken to paint them white or bright yellow. Plastic
streamers are useful for a brief time, but naturally cannot be relied upon for
long periods.
When the vehicle cannot be driven right to the station and a walk
or climb is involved, the track should be clearly marked, and any features such
as streams and cliff faces encountered en route, recorded. An estimate of the
time involved in walking to the station and type of walk involved, should be
noted, i.e., "With 40lb load, 20 minute walk across rocky, scrub covered
ground, thence 40 minutes steep climb along the ridge running NE, through
Lantana, to summit. Brush hook considered necessary to cut walking track."
When camped at the base of a hill it may be necessary to descend
the hill at night, after completing astronomical observations. If such is the
case, the track should be marked clearly with white tape spaced at such a
distance that each piece of tape can be picked out with a torch, from the
preceding one. Remember it is very easy to lose a track among bushes and trees
at night; tracks that appear easy to follow in daylight can become very confusing when seen by
torchlight.
Figure
9.2.
There are various methods of recording field notes, probably the
clearest is to draw a central column in a note book and record, between the
lines, and starting from the bottom of the page, the running mileages
and magnetic bearings of the route being traversed.
On the page to the left of the double lines record all detail
sighted on that side of the route and on the right side notes of all detail on
that side of the track. This method allows plenty of space for recording
detail, and the notes are easily followed.
When taking notes for a very straightforward sketch where little
detail other than road bends, gates and dams etc., is required, mileages can be
written in a line across the page, each mileage having immediately after it, in brackets, notes of the
detail at that point, i.e., 00 (Hillside P.O. go 296° along Pacific Hway), 4.6
(grid 242°), 5.9 (S.P. Jonesville 69m,
Port Dundas 20m), leave H’way, go along Pt Dundas road, 174°) etc.
Figure 9.2 is an example
of column type notes.
With good, clear field notes the sketch can be drawn so that
little in the way of explanatory notes need be attached. Notes on the sketch
should be confined to an explanation of problems likely to be encountered,
rather than "Proceed along Pacific H’way from Hillside P.O. on a bearing
of 296°, passing through a grid
at 4.6, etc. The sketch should clearly show this information at a glance.
The notes, on the sketch, should show such items as rough or
dangerous sections of the track, likely boggy areas after rain, climbing time
on foot, and particularly a description of the feature on which the control
point is located. In areas of heavy regrowth, details of the date of clearing
lanes and the cutting of tracks should be noted, together with an estimate of
the time that they will be useable before being overgrown.
9
3 Drawing Access Sketches
These should be drawn as soon as possible after the field notes
have been taken. As seldom more than 1 station per day is selected when on
reconnaissance, no difficulty should be experienced in drawing a sketch that
evening, while all details of the day’s work are still clear in the mind. There
is no more tiresome task than having to draw some 10 to 20 sketches in a batch,
at some later date. However, the field notes should contain full details so
that sketches can be drawn at any time in the future, or by another person, if necessary.
When drawing access
sketches the following principles should be observed:‑
(a)
All
detail should be oriented with North to the top of the page, and a north point
shown by an arrow.
(b)
It
should be stated that the bearings are magnetic, and that the sketch is not to
scale.
(c)
The
sketch should not be cramped, but should be open and easy to read; some of the
less important details recorded in the notes may necessarily be omitted to
achieve this.
Conventional signs used on Access
Sketches
The following signs are
some of the main ones used in Access Sketches. These are normally bolder than those used on maps.
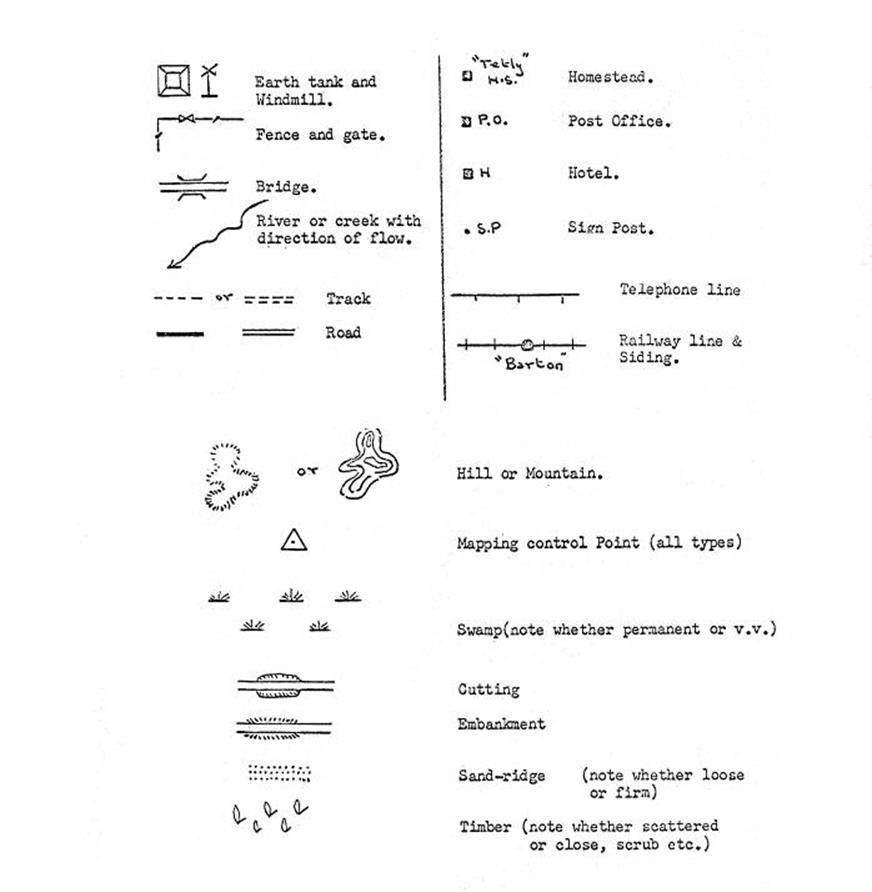
9.4 Helicopter Access
Notes on access made by helicopter should include a description of the
control point, along with a bearing and distance from any prominent features.
Descriptions of the helicopter pad and other useful data should all be noted,
along the following lines:—
"Access was made by helicopter from Higginsfield Airstrip.
The station is situated on a high, windblown sandridge, covered with light
scrub. Initial access was by sky-jinnie to clear scrub and construct pad. The
actual set down point was constructed from logs flown in from Higginsfield.
Regrowth could be expected to make the pad unserviceable by 1971. If a sky-jinnie is
not used the nearest alternative landing point for the helicopter would be
about 1 mile west of the station, with a difficult walk through scrub and rain
forest."
10. Map
reading, including Elementary Aerial Navigation
10.1 Object of Map Reading
This is to render possible the clear and accurate visualization of
the ground, so that this knowledge can be used for whatever task comes to hand. To reach this standard
the student must understand the following:‑
(a)
The
information shown in the margin of the map.
(b)
The
names by which features are known, and technical terms used in mapping.
(c)
Scales,
protracting bearings.
(d)
Map
symbols.
(e)
How to
visualize relief from contours.
(f)
The
difference between true, magnetic and grid north.
(g)
Australian
map grids.
(h)
The
use and reading of Grid (or Map) References.
It must be remembered that few, if any, maps can be perfectly
accurate owing to the time lag between the original aerial photography and the first printing. Although the terrain has been mapped
accurately from the photography constant alterations and additions to the
man-made detail in well populated areas soon renders the best work out of date.
10.2 Understanding maps
(a)
Marginal
information. This varies with the scale of the map, and its purpose. It also
varies slightly with the publishing authority. The information on the margins
of the two scales of maps at present generally used in the field is as follows:-
(i)
ICAO
1:1,000,000.
Name and number of the
area.
Scale.
Elevation unit (ft), and
elevation conversion scale (metres).
Projection.
Hypsometric (Elevation)
Tint code.
Topographic base
reliability diagram.
Scales, Nautical miles,
Statute miles, Kilometres.
Edition number, compiled
by, drawn by, and printed by.
Date of Aeronautical,
Topographical, and Isogonic (Mag. Dec.) Information.
In addition, much information is printed on the back of the ICAO. This includes
symbols for the type of aerodromes, air navigation lights & beacons, marine
lights & code, also miscellaneous
information such as, Isogonic lines, radio heights, prohibited or restricted, areas, etc. These are printed
in dark blue on the face of the map. Hydrographic symbols (pale blue on the
map), relief contours or hatchuring (brown on map) and mapping symbols (black
on map), are also shown.
(ii)
The
1:250,000 map series will probably be the one most used for field work in
Australia for some years. The following information will be found in the
margin:-
Map name, number, series & edition.
Scales in statute miles, nautical miles & kilometres.
Method of elevations shown & datum.
Projection and horizontal datum.
Details of TM grid, zone & spheroid.
Method of giving a map reference.
Magnetic declination information.
Map reliability diagram, and map sheet location diagram.
Map symbol legend.
Date of aerial photography and compilation.
Authority responsible for compilation and printer.
Two important factors to notice about the 1:250,000 map series; firstly
that some map areas have been compiled by different authorities making for some
slight differences in layout and style, and secondly, on these maps the
Australian National Grid, in yards and using the Clarke 1858 Spheroid, is still
in use. As the new 1:100,000 series is compiled, so also will be the new
1:250,000 series based on the metric Australian Map Grid and the Australian Geodetic Datum.
The Universal Transverse Mercator Projection is used.
(iii)
Marginal
information on the 1:100,000 map series is similar to the 1:250,000 series, but
enlarges on it along the following lines:-
Road classification shown.
True, Magnetic and Grid North shown in diagrammatic form.
Information about contour intervals.
Conversion table, metres to feet.(to convert metric heights to
feet).
More specific information about accuracy of horizontal control.
(b)
Names
by which features are known and technical mapping terms.
Basin: A small area of
level ground surrounded or nearly surrounded by hills. Or a district drained by
a river and its tributaries.
Saddle: A neck or ridge
of land connecting two mountains or hills. It is lower than the points it
connects and higher than the surrounding plains and valleys.
Crest: The general
line formed by joining the summits of the main ridge of a chain of mountains.
Or the top of a mountain, or hill.
Dune: A hill or ridge of sand formed by the Wind.
Estuary: The tidal mouth of a river.
Escarpment: An extended line of cliffs or bluffs.
Foreshore: That
portion of the shore between high and low water et maximum spring tides.
Gorge: A rugged and deep ravine.
Knoll: A low detached hill.
Main Feature: Those
important features such as ridges, drainage systems, etc., which determine the
shape of the terrain.
Pass: Narrow passage through mountains or hills.
Plateau: An elevated plain.
Gully: Also
Re-entrant. This is where the hillside is curved inwards towards the main
feature. They are always found between two spurs.
Spur: A projection
from the side of a hill or mountain generally with a decreasing gradient.
Watercourse: The
line defining the lowest part of a valley, whether occupied by a stream or not.
Watershed: A ridge of
land separating drainage systems; the summit of land from which water divides
and flows.
Undulating ground: Ground which alternatively rises and falls
gently.
This list does not profess to be exhaustive. There are many common
words such as hill, mountain, river plain, island cliff or ravine, etc., which
it is not necessary to define.
Technical mapping terms:-
Bearing: True bearing is
the clockwise angle from the true north line to the point observed.
Magnetic bearing is the clockwise angle from the magnetic north
line to the point observed.
Grid bearing is the clockwise angle from the grid north line to
the point observed.
Contour: This is an
imaginary line on the surface of the ground at the same height above sea level
throughout its length.
Contour Interval: The
difference in level between two adjacent contours.
Datum Level: The level to which altitudes are referred.
Detail: All minor natural or artificial features.
Fixed Point: A point
which has been joined to one or more of the main control points by traverse,
intersection resection, etc.
Form Line: An approximate contour; a sketch contour.
Grid: A system of
East-West and North-South parallel lines which represent progressive distances
east and north of a fixed point of origin.
Grid North: The Central
Meridian of a Map Zone points both true north and grid north. Within that Map
Zone any line drawn parallel to the Central Meridian points grid north. The greater the distance
east or west of the Central Meridian, the larger the convergence from true
bearing. This is known as Grid Convergence.
Hachuring: A method of
representing hill features by shading in short disconnected lines drawn directly down the slopes in the direction of the flow of water from the slopes.
Horizontal Datum: The datum to which the horizontal control is
related.
Latitude: The
Latitude of a place is expressed in degrees, minutes and seconds of arc, north
or south of the equator as the case may be. Lines of equal Latitude are
parallel to the Equator hence "Parallels of Latitude".
Longitude: The
Longitude of a place is expressed in degrees, minutes and seconds, east or west
from the Meridian of Greenwich, as the case may be.
Magnetic Declination: The
amount Magnetic North declines from True North, at any place. It is called East
or West declination according to whether magnetic north is East or West of true
north from that place.
Orienting a map: When a
map, sketch,
air photo or plan is placed so that its true north line points true north the
map is said to be "oriented".
Plotting: The
process of recording on a map or plan, the field observations and measurements.
Resection: A method of
fixing the position of the Observer by drawing lines to, or observing bearings to, at least two previously fixed
points.
True North: This is the direction of the North Pole from the
observer.
Vertical Interval: This is the vertical distance between two
contours.
(c)
Scales
and protracting bearings
The word "scale" means the proportion which the length
between two points on a map bears to the horizontal distance between the same
two points on the ground; thus if the distance between two houses on the map is
one inch and the horizontal distance on the ground is one mile, the scale of
the map is one inch to one mile. This can also be expressed as a Representative Fraction. This
expresses the denominator of the fraction in the same unit as the numerator;
thus the R.F. for one inch to one mile is expressed 1:63,360, there being
63,360 inches per mile. As the metric system comes more into use, more scales
will be expressed as a Representative Fraction.
Protracting bearings from
a map has been fully described in 5.1.5.
(d)
Map
Symbols (Conventional Signs)
For ease of recognition, these are suggestive of the object represented. Thus the sign for a
windmill could scarcely be taken for anything else as also a cross for a church
and an aeroplane for an airstrip. The scale of the map governs the space available, therefore a set of map symbols is designed for each map scale. However, little trouble is
experienced in understanding the variations encountered.
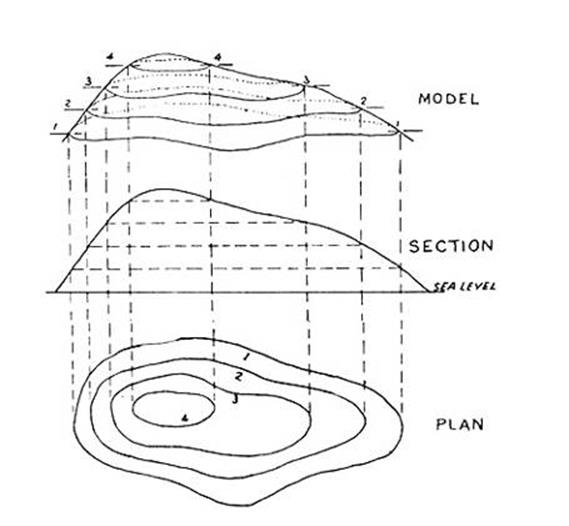
Figure 10.2(a).
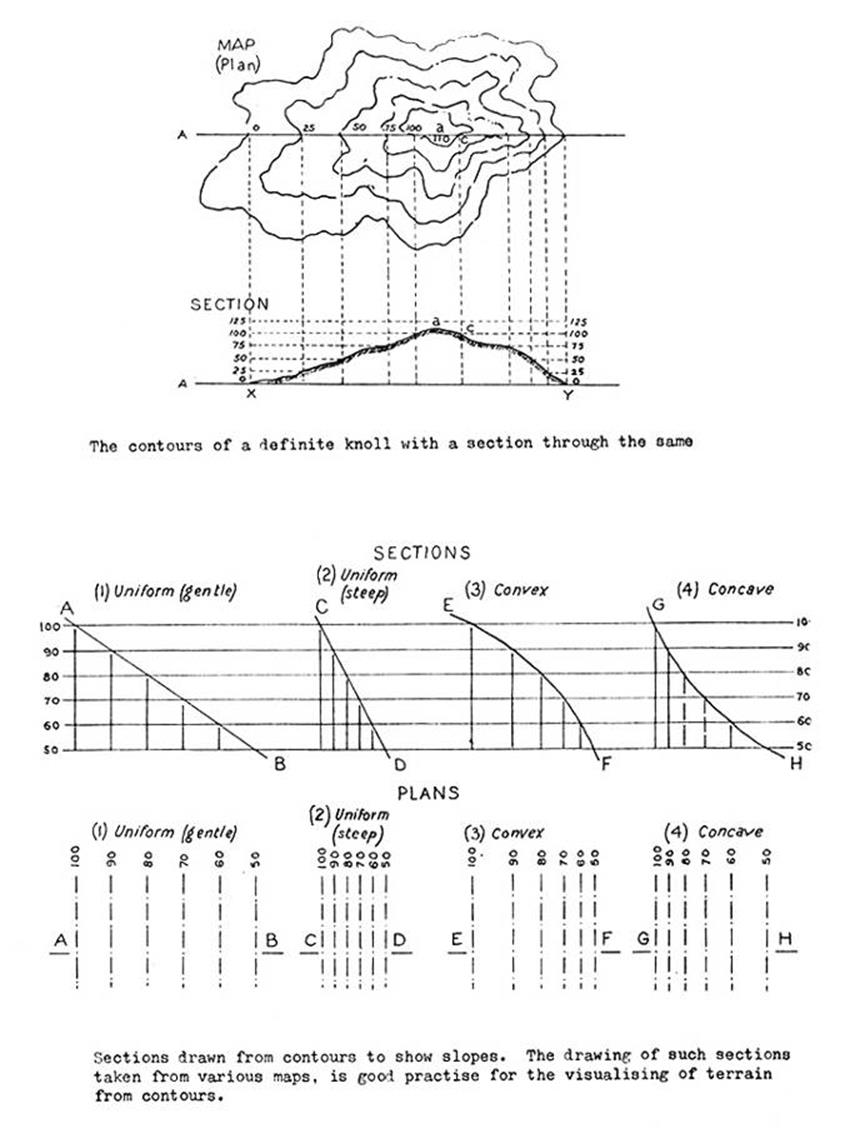
Figure 10.2(b) & (c).
(e)
How to
visualize relief from contours
Relief is mostly shown on the 1:250,000 maps by hill-shading owing
to the lack of
vertical
control in most areas. However maps of more developed areas are contoured at
250ft intervals with layer tinting as an adjunct.
Form Lines are approximate contours and are used when insufficient
vertical control is available for contouring. They show the elevation in the
same manner but are not reliable for exact information.
With increased vertical control becoming available, the new
1:100,000 maps will be contoured in metres. Some have already been published,
the contour interval being 40 metres with 20 metre auxiliary contours in selected areas.
The contour lines have their height printed at various places
along the actual line and these contour lines, with the actual drainage pattern
give the map reader
the picture of relief. As can
be imagined, un-numbered contours of a knoll without any drainage pattern could
also be interpreted as a depression. It should also be noted that the closer
the contour interval,
the better
the picture of relief.
Figure 10.2(a) below shows a contour plan of a knoll and section
through the same. As previously mentioned, unless some other information such
as heights against each contour, drainage pattern, spot heights, etc., is
provided this plan could just as easily be that of a depression. Turn the page
upside down and see.
(f)
The
difference between true, magnetic, and grid north
True north means the direction of the north pole from the observer and the
direction of true north from the observers position is called the True
Meridian. As the earth is spherical in shape, it follows that the Meridian of
any point, East or West of the observer’s position will meet the true meridian
of the observer’s position at the north pole.
Magnetic north is the direction of the magnetic pole from the observer’s
position. The difference between the magnetic and true meridians is known as
the Magnetic Declination of that position. Magnetic Declination varies from
place to place throughout the world. Figure 10.2(f) shows the general pattern
of magnetic declination over the Australian continent. Lines joining places of
equal magnetic declination are known as Isogonic Lines. Owing to the slight
annual movement of the magnetic pole the magnetic declination of a place varies
slightly from year to year. See also 5.1.3 - Magnetic Declination.
Grid north. Map grids will be explained in the next section. For a definition
of grid north it is sufficient to say that grids are rectangular and only one
grid line coincides with a true meridian therefore it is only along this
meridian (called the Central Meridian) that the grid points to true north. All
other vertical grid lines are drawn parallel to this Central Meridian and do
not point to true north, but in each case point to an imaginary point called
“Grid North”. The angle between True & Grid north is called Grid
Convergence and increases as the distance from the Central Meridian increases.
Figure
10.2(f). Isogonic Chart of Australia.
(g)
Australian
Map Grids
In the early 1930s the Australian National Grid on the Transverse
Mercator Projection, and in yards, was adopted for Australian maps, and maps
produced until the completion of the provisional and 1st Edition of the
1:250,000 maps about 1966 use this grid. Any revising to these 1:250,000 maps
will be only overprints in magenta to show changes of road and track patterns,
built up areas, development, etc. This grid is based on Clarke’s 1858 Figure of
the Earth, and the Astonomical Coordinates of the Sydney Observatory were used
as the origin. 8 zones, each 5° wide plus ½° common overlap were laid out to cover from Longitude 111°E to
154°W.
The True Origin of the coordinates of each zone in the grid is
junction of Latitude 34°S and the Central Meridian of the zone. The False
Origin for each zone, with zero coordinates is 400,000 yards west and 800,000
yards south of True Origin. This is to ensure that coordinates for all points
within the zone will be positive.
In 1965, the Australian National Mapping Council adopted a new grid, the Australian Map Grid. It is
a metric grid based on the Universal Mercator Projection and the Australian Geodetic Datum. 12 zones, 6° wide plus ½° common overlap are used
to cover the Australian continent and Territories under its control.
True Origins are the junction of the Central Meridian of each zone
with the Equator. False origins are 500,000 metres west and 10,000,000 metres south of the True Origin.
Figure 10.2(g) shows the layout of the map zones under both the
Australian National Grid and the Australian Map Grid.
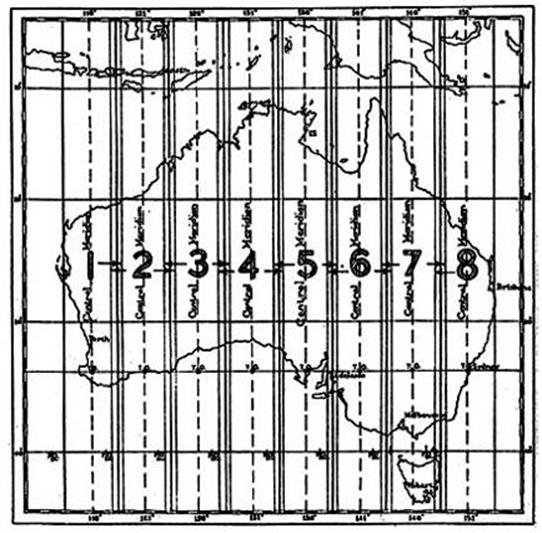
Figure
10.2(g).
Transverse
Mercator Zones of the Australian National Grid.
T.O. True
Origin
F.O.
False Origin (400,000yds West, 800,000yds South of T.O.
Zones
overlap ½° on each side.
(h) The use and reading of
Grid (or Map) References
(i)
The
1:250,000 Australian National Grid (yards). It will be some years before this
series will be republished on the Australian Map Grid (metric), and as these
maps are the basic map for current field work any grid references used will
still be in yards. However, this is no problem as all maps incorporate a panel
in the margin giving an explanation and an example. The black numbered grid
lines indicate 10,000 yard intervals, and the Grid Reference of a point is
given to the nearest tenth of this interval, i.e. 1,000 yards. Each grid line
is numbered with two figures, the 100,000 and the 10,000. Thus the three
figures for the Easting reference come from the two printed figures on the
nearest line west of the station with the third figure representing the number
of tenths the point is estimated to be east of that line.
It follows that the three
figures for the Northing reference come from the two printed figures on the
first grid line immediately south of the point, with the third figure
representing the number of tenths the point is estimated to be north of this
line.
(ii)
The
1:100,000 Australian Man Grid (metric). As these maps will gradually become
available an explanation of the giving of Grid References on these maps, is
warranted. The black numbered grid lines indicate 1,000 metre intervals. By
estimating the tenths of these intervals in the same manner as in (i) above, a
Grid Reference to the nearest 100 metres is obtained.
From the margin and the
Grid information panel ascertain within which 100,000 metre square the point
lies, and prefix the six figure reference with the two letters nominating that
100,000 metre square. See Figure 10.2(h) for examples of Grid References on
both the 1:250,000 map and the 1:100,000 map metric grids.

Figure
10.2(g). Zone Boundaries, noting Zones overlap ½° on each
side, and selected Central Meridians, noting that the intersection of each
Central Meridian and the Equator is the True Origin. False Origins are not
shown.
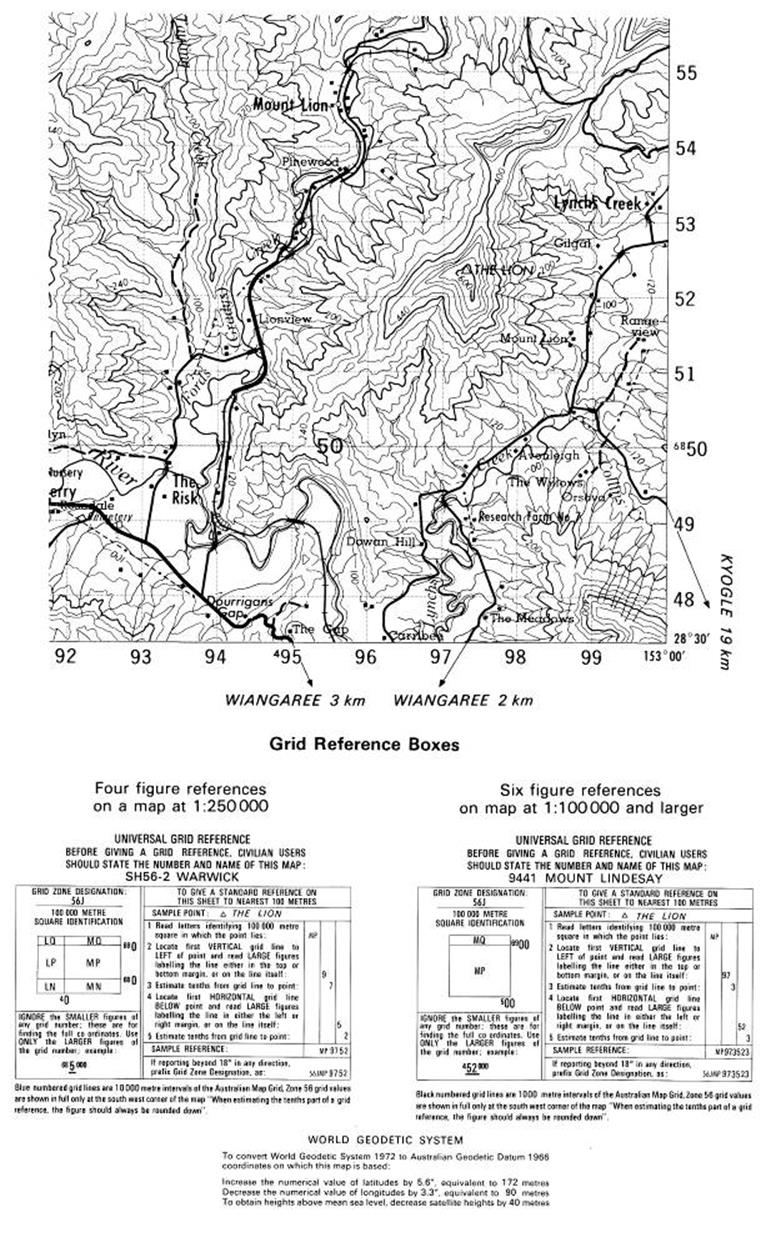
Figure 10.2(h)
10.3 Hints on Map Reading
Once a good knowledge of the amount and variety of information
obtainable from the map has been assimilated, map reading itself is mainly a matter of having plenty of practise at following maps under
field conditions. The following hints have been found useful:-
(a)
Always
check the date of the air photography, map compilation and latest amendments. These will
give an idea of
the reliance to be placed on that particular map.
(b)
Always
have a prismatic
compass, protractor,
and scale handy. If no scale is available make one along the edge of a piece of
blank paper.
(c)
Always
keep the map orientated.
(d)
Always
use a soft lead pencil (not a ballpoint) to draw in bearing or make notes of
directions and mileages. It is a great help to be able to quickly plot one's position, particularly when on
reconnaissance. When this is done in pencil the map can be cleaned up later and the required data only plotted
permanently in ink. Also always have a notebook
handy for
more elaborate notes.
(e)
When “feeling the way” in poorly
mapped country or along tracks not shown on the map, always keep, a speedo and
magnetic bearing log. At the end of the day correct bearings to true and plot
the days travel as accurately as possible on the map. The information gained is
often necessary to help prove lines plan the next day’s moves, or to update the published map.
(f)
Finding
approximate north from analogue watch and sun (Southern Hemisphere) : Lay the
watch flat, point 12 to the sun, north lies mid-way between 12 and the hour hand. The
method is quite rough, but is often useful.
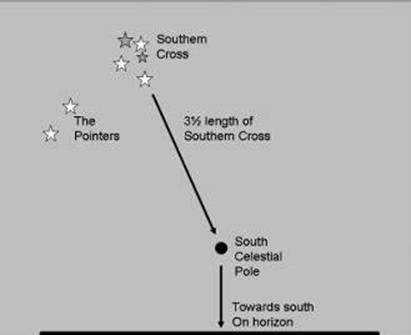
Figure.10.3(g).
(Not to Scale).
South
Celestial Pole is elevated above the horizon by an amount
equal to
the Latitude of the observer’s position.
(g)
Finding
approximate south from the Southern Cross : Imagine the Southern Cross as a
kite, estimate the length of the greater axis and extend this axis from the
tail of the kite about 3½
times. The point reached is the South Celestial Pole, i.e. a point true south
of the observer, elevated above the horizon by an amount equal to the Latitude
of the observer’s position. See Figure 10.3(g).
10.4. Elementary
Aerial Navigation
(a)
Standard
required in the field
The main requirement is to navigate a light plane on
reconnaissance or Aerodist flights, or a helicopter to establish or visit
Mapping Control Points.
Therefore ability to follow terrain mainly from the 1:250,000 map
and air photo's is needed rather than any knowledge of radio beacons,
application of drift to courses, flight plans, etc., which can safely be left
to the pilot.
(b)
At
times it may be necessary to use the ICAO maps, but where possible the
1:250,000 series should be used. A protractor and scale (or set of dividers),
are necessary. The pilot will estimate drift wind speed, etc. He will apply the
drift so as to keep the correct course, altering it when necessary during
flight, and will estimate his speed over the ground, in knots, from this point
on, ground speed should be converted to flying time in minutes and this
should be the basis of all Aerial Navigation.
Usually the pilot will be a good navigator, however the passenger
will need to follow his own maps so as to perform his various technical tasks.
(c)
Prior
to the commencement of the flight, plot the course to be followed on the map and mark off the points as they
will be reached, in time intervals.
Once the flight commences, mark the time each point is reached
with a soft pencil thus enabling a close estimate of the time of' arrival at
the next point of detail.
Concentration is the main keynote; if in doubt of the aircraft's
position never worry about detail already passed, watch the terrain ahead and
concentrate on locating some point which will positively identify your
position. If on a low level flight and in doubt, immediately take the aircraft higher;
it is amazing how
much easier
locating the position becomes at 3,000 feet above ground level.
(d)
If the
final approach to a point is to be made on air photos, mark the boundary of the
area covered by the photos onto the map and once the aircraft reaches that boundary, follow the photographs
exclusively.
(e)
The
1:250,000 maps give a fair amount of natural detail even in many unpromising
areas. Probably the drainage pattern gives the best navigation aid. Even in
endless sandridge country a clear pattern is there to be followed by a
keen-eyed navigator who can really concentrate.
(f)
Most
difficulty will be experienced in flat, featureless areas with no drainage
pattern, or man-made detail such an earth tanks, etc.
Often a long flight across such terrain is necessary to site, or
visit, a mapping control point. In this case initial preparation should ensure
wide aerial coverage of the area. The aircraft’s course should be plotted to
the most easily identified point on these photos, with a short separate course to
the mapping control point. Once the identifiable point is located there is no
doubt as to one’s position thus giving a better chance of locating the control
point at the first attempt.
10.5 The
Use of the Plane Table
With the plane table the detail of an area can be mapped
graphically as it appears before the observer. It was used extensively prior to
the adoption of photogrammetric methods. Plane table mapping over small areas has some
important advantages:-
(i)
All direction measurements are
instantly recorded on the map. The intervening processes of recording field
notes and plotting them are eliminated.
(ii)
The map is constructed at
once, in the field, so that no permanent records are necessary, other than the
map itself.
(iii)
The
topographer sees the undulations of the ground that he is mapping. He can draw
a good representation of the contours and he uses fewer field observations.
(a)
The
principle of mapping with the plane table
The plane table is a drawing board mounted upon a tripod and
capable of rotation in a horizontal
plane. The essence of the art of plane tabling is that the board should be so
oriented that directions upon it are identical with corresponding directions
in nature. When this orientation has been achieved, rays from a known
point, representing directions in nature, can be drawn upon the board.
By means of intersecting rays, drawn from different known positions, or by
distances measured along a known direction, points of detail in the countryside may be transferred to the paper.
(b)
The
plane table and ancillary equipment
(i)
The
plane table
is usually rectangular and about 18" x 24". It is made of light, well
seasoned timber and has a screw thread which enables it to be mounted on a tripod
and rotated or clamped in position, as required. It is contained in a canvas
cover which has straps on the back for carrying on the shoulders.
(ii)
The
plane table tripod may be of the "Johnson Head" type which allows quick
levelling of the plane table, or it may be of a very light construction with a
rigid head and the plane table is levelled by the placing of the legs. The
"Johnson Head" type is easy to use but is heavy to carry, the lighter
type is thus probably the best for general use as one soon gets used to
positioning the legs to quickly level the plane table.
(iii)
The
sight rule or alidade consists of a straight edge, made of non-magnetic metal, to each
end of which is attached a vertical arm. One vertical arm has an eye-slot, and
the other acts as a frame for a taut sighting wire. The distant object is
observed through the sighting-slot and aligned against the sighting wire; thus
directions in nature may be transferred to the board as pencil lines. The
straightness of the ruling edge should occasionally be verified by ruling a line and then reversing
the ruling edge end for end.
A parallel arm is a convenience, the edge of the rule then being
positioned close to, but not on, the plotted position of the point being
sighted. Once the point has been sighted, the parallel arm is moved exactly
against the plotted point, and the direction drawn.
If the alidade has no parallel arm, its edge should be positioned
against the plotted point by laying a pencil, on its side, with the blunt end
exactly coinciding with the plotted point. The edge of the rule is kept against
the end of the pencil while bringing the sight onto the distant point. Check
that the rule is still on the plotted point and draw the direction.
In short the alidade takes the place of the theodolite to obtain
horizontal directions.
A telescopic alidade is available, however these are cumbersome
and would not normally be carried around for close detail work. Their main use
would now be for contouring where the stadia marks and a staff could speed up
the locating of a close network of spot heights.
(iv)
The
"Indian" pattern Clinometer consists of a level bubble in a frame with a vertical arm at each
end, one arm contains a peephole and the other has a sliding vertical sighting
wire and scale of natural tangents, to 2 places of decimals, with their
corresponding vertical angles. The bubble is levelled with a thumb screw, the
distant object is sighted through the peephole, and the sighting wire brought
into coincidence with the object. Check that the bubble is still central and
read the natural tan of the angle, estimated to 3 decimal places, from the scale. This tan, multiplied by the scaled
distance from the plane table, gives the difference in height, to plane
table level; correct it to ground level. From this it can be seen that the
actual angle is rarely needed and therefore rarely recorded.
An Abney level can be used instead of the "Indian"
clinometer with probably slightly more accurate results; however, in this case,
a Table of Natural tan's of angles would have to be carried.
Before commencing field operations, the "Indian"
clinometer, or Abney level, should be checked against a theodolite read
vertical angle and adjusted if necessary. Further checks, during extended field
operations are advisable.
(v)
A
good quality scale is a necessity. One graduated in millimetres and about 300mm long
will now suit all tasks unless some specialized scale is required. In plane
tabling, the scale lakes the place of computations for obtaining distances.
(vi)
The
Trough Compass consists of a magnetised needle about 6" long, suspended in
a rectangular container. This is usually housed in a wooden box with a sliding
lid. The closing of this lid lifts the compass needle clear of its pivot. When
the orientation of the board has been established with reference to distant
fixed positions, the compass is positioned on the board with its needle on the
central mark; a pencil line is now drawn around the box. This pencil mark and
the compass will approximately orient the board on future occasions in that
area, subject of course to local attraction from fences, vehicles, ore bodies
etc.
(vii)
Binoculars. An average pair of
binoculars of 8x magnification are satisfactory; these will be in almost
continuous use.
(viii)
Pencils. 2H to 6H for drawing
rays, HB for making notes and calculations. Remember that in hot climates
pencils soften slightly; under such conditions the 6H will appear more like a 2H. Pencils should be kept
sharp; a sharpener and fine emery or glass paper are essential. A strip of the
emery paper can be attached beneath the board.
(ix)
Erasers (Rubbers). Both soft and
hard are required. On plastic sheets the hard is more often used than the soft;
no amount of rubbing seems to harm the surface of these sheets.
(x)
Needles. These are required to
prick through points as they are established so that they are not lost when
rubbing out superfluous data.
In addition, at the conclusion of the day's work, the detail which
has been finalized is "inked in". Requirements for this are a selection of
colours in good quality drawing ink which is suitable for plastic sheets, a
"Rapidograph" type pen with a selection of points and a good quality
straightedge. A contouring pen is a great help for this part of the drawing.
(c)
Office
Preparations
Normally arrangements will have been made to have at least 3
control points established in the area. The coordinates of these points will
now be in metres on the Australian Map Grid. These preparations are:-
(i)
Decide
on scale to be used.
(ii)
Draw a
rectangular grid to suit the scale.
(iii)
Plot
the control points on this grid.
Stable based plastic drawing material is ideal for use with the
plane table. When plotted ready for field use it can be attached to the board
with masking tape along each edge. This prevents dust and grit getting between
the board and the sheet. If good quality drawing paper is used it should be
pasted to a
sheet of aluminium before plotting.
(i)
The
scale to be used. This is entirely governed by the task in hand. For mapping
tasks 1:100,000, 1:50,000, 1:25,000, 1:12,500 and 1:10,000 are most often used.
If engineering plans of camps or establishments etc are required these may be
to scales of 1:1,000 or 1:500.
(ii)
Drawing
the grid. The first step in drawing a grid of squares is to construct a
rectangle near the outside edges of the board. It is clear that once such a
rectangle has been drawn, equal distances may be measured off along its sides
and joined with a straight edge to form the grid.
To construct such a rectangle, draw two diagonals roughly from
corner to corner of the plastic sheet which has been out to the size of the
board. In fact it should be cut about 2mm smaller than the board for ease of
sticking down with masking tape so as to provide a perfectly flat surface.
Set a beam compass to strike off arcs of equal distances from the
intersection of these diagonals. These arcs should cut the diagonals about 2 to
3 centimetres from each
corner. Join these and points which will then form a perfect rectangle. See
Figure 10.5 (a).
When the grid has been drawn, check its accuracy by laying a
straight edge across the diagonals of the squares where it must cut all
intersections. See Figure 10.5 (b).
(iii)
Plotting
the control. Each grid line is given its coordinate value in the same manner as
a map. Then the control points are accurately plotted. A good check of the
accuracy of this plotting can be made by comparing the scaled distances between these points and the
actual measured,
or computed,
distances supplied with the coordinates.
The accuracy of the completed map depends on the precision of the plotting of the
control points on which it is based. The utmost care must be taken to ensure
that no error, which can be controlled, is permitted to appear.
(d)
Mapping
with the Plane Table
The four main methods of
obtaining detail with the plane table are :-
1.
Intersection
2.
Resection
3.
Triangulation
4.
Ray
and Distance
Traversing with the plane table is sometimes used. The above
methods will now be described in detail, however, it is important to stress
here that in all the above cases, clinometers heights should be taken and
should be worked out while the board is set up. Naturally these calculations cannot be commenced until
the first 3
way intersection,
resection or triangulation has been completed, so that distances can be scaled. A comparison of the
heights so obtained gives a check on the accuracy of the position of the new
point; in the event of a large difference in the heights a check of the scaled
distances, the plotting and the clinometer readings, should be made.
(i)
Brief
description of general procedure.
All the established control points are visited and rays are taken to all
prominent points of detail. The board must be set up and levelled close to the
station mark. How close depends on the scale to be used and the accuracy one
can plot. Under field conditions the plotting accuracy is about 0.25 of a
millimetre, thus the following table gives some idea of the accuracy which can
be expected.
At 1:12,500 1mm = 12.5m and 0.25mm = 3.1 metres
1:25,000 1mm = 25m and
0.25mm = 6.25 metres
1:50,000 1mm = 50m and
0.25mm = 12.5 metres
1:100,000 1mm = 100m and
0.25mm = 25
metres
If making plans at scales of 1:500: 1:1,000, etc it is necessary
to plumb the exact point on the board over the station mark.
Once the drawing of rays is commenced, notes with thumbnail
sketches are entered against each ray, or alternatively, the rays are numbered
and the details are entered in a note book against these numbers. As mentioned
previously clinometer angles are recorded.
When setting up at the first control point visited the plane table
is, oriented by the identification and sighting with the alidade of one of the
other plotted control point. A check of the orientation of the board and also
of the office plotting is made by sighting in turn each of the other plotted
control points which is visible.
To avoid a mass of insoluable rays on the board, each time a three
way cut has been obtained, the point should be "pricked through" and the
relevant rays rubbed out.
Once the intersecting of points from the control stations has been
exhausted move through the area gathering further detail by:-
Further intersections from
the new points established.
Resections from various
places in the area.
Triangulation.
Ray and Distance.
"Inking In" should be a gradual process; at the
conclusion of each day's work sufficient "inking in" should be done
to ensure no detail is lost.
Once sufficient spot heights have been obtained contouring should
be done in the field with the terrain in view. Methods are elaborated
upon towards the conclusion of these notes.
The methods of obtaining detail:
1.
Intersection.
This is the most accurate method and thus yields the best further control
points. It is easy but a few
precautions should be taken:-
(a)
Orient
the board carefully by sighting the most distant control point.
(b)
Make
sure the board is properly clamped.
(c)
Check
orientation by sighting another control point.
(d)
Draw
the rays in the direction of the point being intersected. Do not draw it right
into the observer's plotted position or a mass of converging lines will result.
Number the rays and make thumbnail sketches and notes.
(e)
Check
that the board has not been moved by resighting one control point.
(f)
Lay
trough compass on the board with needle on the north mark and draw a
"box" around the compass. This "box” will be used, later on, to
approximately orient the board at resection points. A check of this
"box" can be made at the other control points to ensure that it was
not drawn at a station where a large amount of local attraction upset the
compass needle.
(g)
Take
clinometer heights; calculate, if distances can be scaled.
Intersections, also resections and triangulation, do not give very
accurate results if the angles are small, try and keep the angles over 30° and under 150°. See Figures 10.5(c) and
10.5(d).
While taking as many rays as possible, the beginner should take
care to avoid covering his board with a dense and insoluble network of rays.
At least 3 rays
are necessary to fix positions which are to be used for subsequent control.
Positions fixed by 2 rays can only be accepted for mapping detail and then
only when, there is no reasonable doubt of identification. However, if a
point on which a 2 way cut has been made, is visited and checked by
triangulation, its accuracy is probably as good as a three ray intersection, if the angles are all over 30° or under
150°.
If the observer sees a point which he intends to visit, a ray can be
taken to it. This is known as an “Azimuth Ray”. On
visiting the point, the alidade can be laid along the azimuth ray and the board
oriented accurately by sighting the control point. This helps considerably when
doing resections. If the ray is short, a further length should be drawn in the
margin as the alidade cannot accurately be laid along a very short line which,
in turn, causes the board to be inaccurately oriented.
Remember that intersections possess the great advantage that they
enable the points to be fixed without visiting them thus saving a great deal of
time and often a great deal of walking.
2. Resection. This is the
term used for the process of fixing a position from at least 3 previously fixed points,
without actually visiting them.
(a)
Trough
Compass Method: Orient the table with the trough compass, clamp it, sight the 3 fixed points and draw
back rays from their plotted positions on the board towards the observer's
position which is unknown, at this time.
These rays (unless the original orientation has, very luckily,
been correct) will produce a triangle on the board, i.e. the "triangle of
error". This is because the orientation of the board is not accurate, and
it follows that the orientation error (in angle) of each ray is the same. There
are certain set rules for solving the triangle of error. Firstly there are 2
cases:-
Case 1:
If the observer is within the triangle formed by the 3 fixed points in nature,
then his position on the board will be within the triangle formed by the rays on the board. His exact position within
the triangle is determined by the condition that its distance from each of the rays is proportional to the length
of these rays, i.e. nearest to the shortest ray, furthest from the longest ray and intermediate from the
intermediate length
ray. See
Figure 10.5(e).
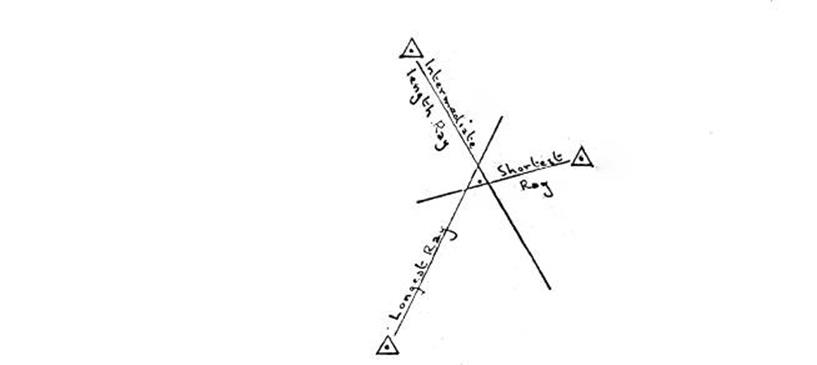
Figure
10.5(e) : The observer's position is within the triangle of error.
Case 2:
If the observer is outside the triangle formed by the 3 fixed
points in
nature, then his position on the board will be outside the triangle formed by the rays on the board. There are 6 sectors
formed by the rays; however, all but 2 of these sectors can immediately be discarded because, when facing
the fixed points, the observer’s position must be in one of the 2 sectors where all the rays are either to his right, or to his left.
A foolproof method of deciding on these two sectors is to consider the rays as 3
spears pointing away from the control stations. The two sectors in which the thumb and
fingers would go to pick them up as a bundle are the sectors in which all the
rays are either to the right or to the left of the observer. See Figure 10.5(f).
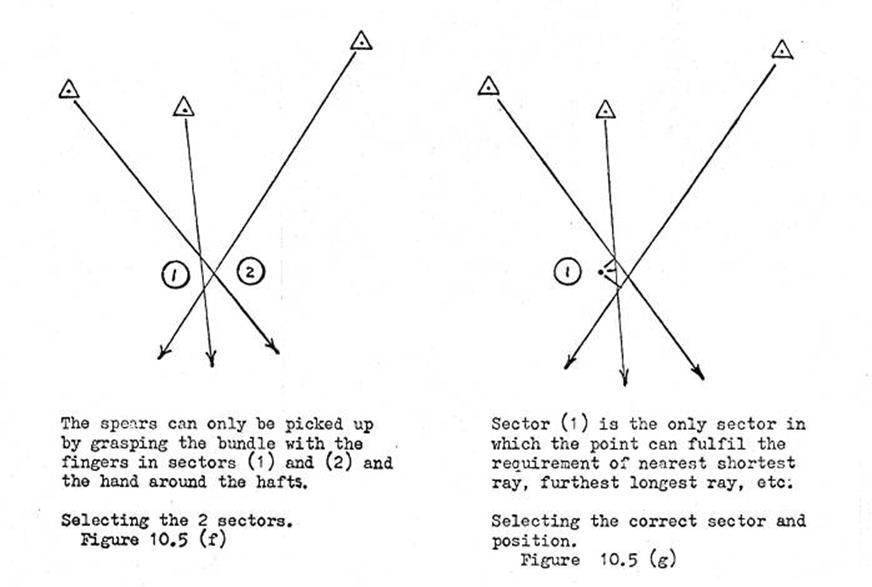
The one sector, of these two, in which the point actually lies,
will be the one where it can be nearest the shortest ray, furthest from the longest ray, and intermediate from the
intermediate length ray. See Figure 10.5(g).
The next step in both Case 1 and Case 2 is to estimate the
observer's position on the board in relation to the triangle of error, mark it,
rub out the rays forming the triangle, lay the alidade along a line from the
estimated position to the most distant control point, reorient the board by
sighting the control point and clamp it.
Again draw the 3 rays which now may give a perfect cut, or more likely, a much
smaller triangle than the original one. Repeat the operation until no triangle
is formed. Prick through and clean off the redundant rays.
Resection is most accurate when the observer's position is inside
the triangle formed by the 3 control points (Case 1). If the observer's
position is outside the triangle formed by the 3 control points, the best
results are obtained when the angle
between the extreme
rays is
large; 60° is rarely more than fair whilst nearly
180° is good. Obviously 180° would mean that the point is exactly on line between the 2 control
points and this should give an accurate resection if the third ray cuts this
line at an angle between about 50° and 130°.
Generally speaking, with control points of equal value, fix the
new position from
the nearest points
but orient the board from the more distant points.
Once sufficient detail has been plotted, it is often unnecessary to resort to the
trough compass
to orient the
board. A good first approximation can be obtained from plotted detail such as
fences, power or pipe lines roads, etc.
(b)
Tracing
Paper method:
A piece of
tracing paper
is laid
anywhere on the board, which does not need to be oriented with the trough
compass. Sight 3 control
points in turn, drawing rays from each on the tracing paper, which must not be
moved in the process. A tiny hole, about the same size as the point of the
plotting pencil, is made at the intersection
of the rays on the trace.
The trace is then fitted over the plane table plot in such a way
that each ray passes through the plotted position of the control point to which it refers. The observer's
position on the board will be at the intersection of the 3 rays on the trace; mark
this position on the plane table through the tiny hole in the trace. Orient the
board by sighting one control point and check with the other two control
points.
The difficulty of carrying sufficient large size tracing paper and
handling it in the
wind detracts
from the usefulness and accuracy of this method. However, particularly for the
beginner it may, with advantage, be used for a first approximation which will often be the correct solution.
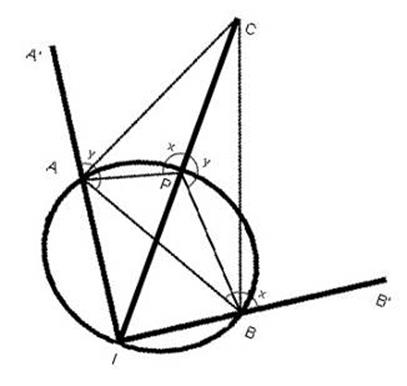
Figure
10.5(h)
(c)
The
Collins Point Method (Bessel’s Solution). This method is attractive in that it
requires no successive approximation, and once mastered is quite quick.
Consider the diagram 10.5(h), A, B and C are the control points and P is the
observer's position which is at present unknown. The theoretical basis of the
method is; AB is chosen as the base and the circle ABP drawn. CP is produced to
meet this circle at the Collins Point I. Thus if the position of I can be
located the direction of IC and therefore PC is known and the table can be oriented. In
practise, the circle is not drawn.
In figure 10.5(h)
APC = x BPC = y
BAI = BPI =
180°-y
Therefore A¢AB = y
Similarly B¢BA = x
In practise it is the positions of these points plotted on the
board which are used and in the following explanation lower case letters, a,b
c, etc, will be used to indicate the plot and upper case letters A,B C etc, to
indicate the points can the ground.
From the example shown in Figure 10.5(h); on the board the
position of I is found with respect to a, b and c. Its position will be given
by the intersection of the lines aa' and bb'. These lines are obtained by
plotting y at a, and x at b. This is simply achieved as follows:- (Remember
that the board is at P)
1.
With
the alidade
pointing along
ab turn the board until B is sighted and clamp it; this makes abB a straight
line.
2.
Draw
in a ray from the control point not used as the
base, that is from C, through the position a. This is the line a'a. The plotted point c is not
used until step 6.
3.
With
the alidade along ba sight on A and clamp the board, this makes baA a straight
line.
4.
Draw
in a ray from C, through the position of b. This is the line b'b.
5.
a'a
and b'b are produced to meet at i.
6.
The
alidade is laid along ic and the board rotated to sight C and clamped. The
board is now oriented.
7.
Rays
are now drawn from A through a, and from B through b. These should intersect ic
at the position p.
From the foregoing it can be seen that the board has to be clamped 3 times
after sighting stations; this has to be done with care or a poor fixation will
result.
A little experience is required to choose the correct base, not only to give the
best fix, but also to ensure that the point i falls on the board. An
interesting case arises when CP is a tangent to the circle ABP, in which case i
and p coincide, though a solution is still possible.
(d)
Danger
Circle. All methods of resection fail when the circle which passes through the three
control points also passes through or very close to, the position to be fixed. When this occurs points are said to be on the "Danger
Circle" and all plane table operators should be on their guard against
this possibility. See Figure 10.5(i).
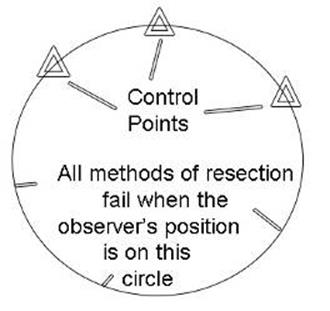
Figure
10.5(i).
3.
Triangulation.
When sorting out the rays from the various control points it will often be
found that there are quite a few points to which only 2 way cuts were obtained.
To ensure that the same point was indeed sighted from both
stations it is necessary to visit such points. Set up the board and orient by
sighting one of the two control points visible along its appropriate ray; clamp
and sight the second control point. If the alidade coincides with the ray
originally drawn from this control point, the intersection of the rays is the
accurate position of the observer, Subject of course to the triangle being well
proportioned.
4.
Ray
and Distance. Detail close to any point established is gathered by ray and
distance. At most mapping scales and over distances of 100 - 200 metres pacing
is usually sufficiently accurate. It is considered that, with practise, an
accuracy of ±3 metres per 100 at the
very worst
should be expected. No attempt should be made to pace an exact metre; pace
naturally and calibrate these paces against a 100 metre chained distance. This
calibration should be done in similar terrain to that being mapped.
If a person paces 114 to the 100 metres this gives 1.14 paces per
metre therefore:-
Number of paces /1.14 =
Distance in metres.
Minor Methods of Obtaining
Detail
The "Position Line" and "Cutting; In"
This can be roughly described as a combination of intersection and
resection and can be very useful in obtaining extra detail once a reasonable
amount of control has been accumulated. All that is needed is to get exactly on
line between 2 control points, or on the prolongation of such a line, or
along the straight
line of a road, a power or pipeline which has been accurately plotted.
Orient the board along such a line, sight with the alidade a
control point as near to right angles as possible to this line, then the point
where this ray cuts the position line is the observer's position. Where
possible, sight a second control point as a check. This method is very suitable
for fairly quickly obtaining extra spot heights, for contouring.
Traversing with the Plane Table
Sometimes sufficient detail cannot be obtained by the previously
mentioned methods owing to timber cover or flat terrain etc.
In such cases it may be necessary to resort to traversing. It is
slow and very liable to the accumulation of error, because every error of measuring
distance, or of orienting the board is carried forward.
To be satisfactory the traverse must close on another control
point, or be in a loop closing on the starting point. In this way gross error
can be eliminated and accumulated error adjusted out. Proceed as follows:-
1.
Set up
and orient the board at some known point.
2.
Draw a
ray to a point in the required direction, pace (or chain) the distance.
3.
Go to
the new point, orient the board on the back ray to the point just vacated.
4.
Draw a
ray to another point in the required direction and again obtain a distance -
and so on, until the traverse is completed.
It is clear that laying marks such as ranging poles will often be
required at the rear and forward stations, making the task slow and cumbersome
and a task for more than 1 person. Thus traversing is a poor substitute for any
of the other methods of obtaining detail with the plane table.
Orientation of the board is entirely governed by the back ray.
Such rays, when drawn must be extended by short lines near the extreme edges of
the board to give maximum length for
each orientation.
As the traverse will have to be adjusted it is advisable to plot
it at twice the scale on a sheet of paper which has been gridded to twice the
scale. This plotted traverse is then adjusted geometrically to the required
length and swung into correct orientation and the resultant adjusted traverse is plotted onto the plane
table. See Figure 10.5(j).
To adjust the traverse, a line A,b,c,d,e, is plotted equal to the
total length of the traverse. At e, a line eE is drawn at right angles to Ae,
and equal to the traverse misclosure. Draw a line joining points A and E. Perpendiculars are then
drawn to meet this line from the intermediate points b,c and d. The distances bB, cC, dD and eE are the
adjustments to be made to the field plot of the traverse. The direction of
these adjustments is parallel to that of the original misclosure at E.
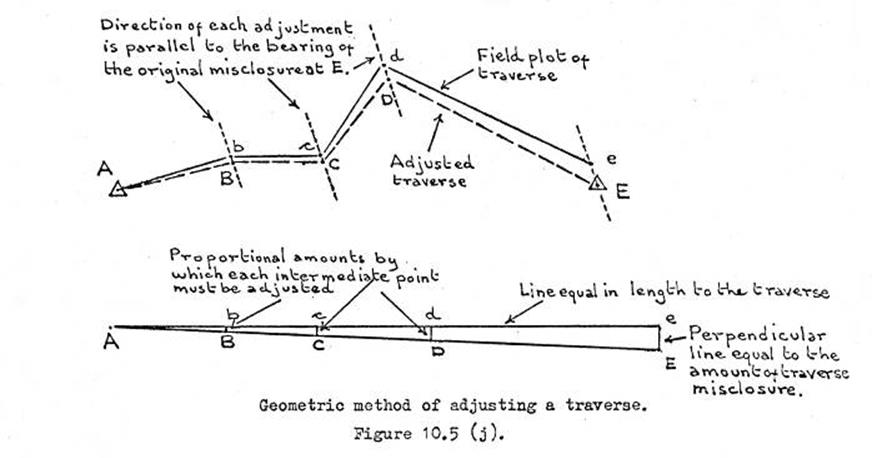
Figure
10.5(j). Geometric method of adjusting a traverse.
Contouring with the Plane Table
A network of spot heights must be built up to cover the area and
no control point
should be
established without obtaining a height. The density of the coverage depends on
the contour interval to be plotted and the type of terrain. Where the contour
interval is close and there is a lot of relief, the spot heights will need to
be closer than if the country is fairly flat. When the contour interval is wide
many less spot heights are needed. In this case contouring can often proceed as
detail is being built up.
When the contour interval is close this is not practicable and it
is usually necessary to get a considerable number of spot heights on the slopes
of the high points. This is best done by running a series of lines of heights
down the sides of the hills. Various methods can be used to obtain these
heights depending on the equipment available, i,e. level and staff, theodolite
and stadia, theodolite and chained distance, clinometer and chained distance,
or even clinometer and paced distance.
If these spot heights are on line to the distant control points,
or down the spines of prominent spurs it is a help in the plotting and the
later sketching of the contours. Once these spot heights are plotted sketch in by eye any local drainage
pattern, then the contours also by eye, using the spot heights as control. By
so watching the terrain as the contours are being sketched very many less spot
heights are needed to obtain a good representation or the relief. Each of the
high points is, in turn, treated in this manner. Thus a good picture of the
relief over the area is built up, enabling a quick assessment of any extra spot
heights that are needed to complete the
contouring of the lower areas.
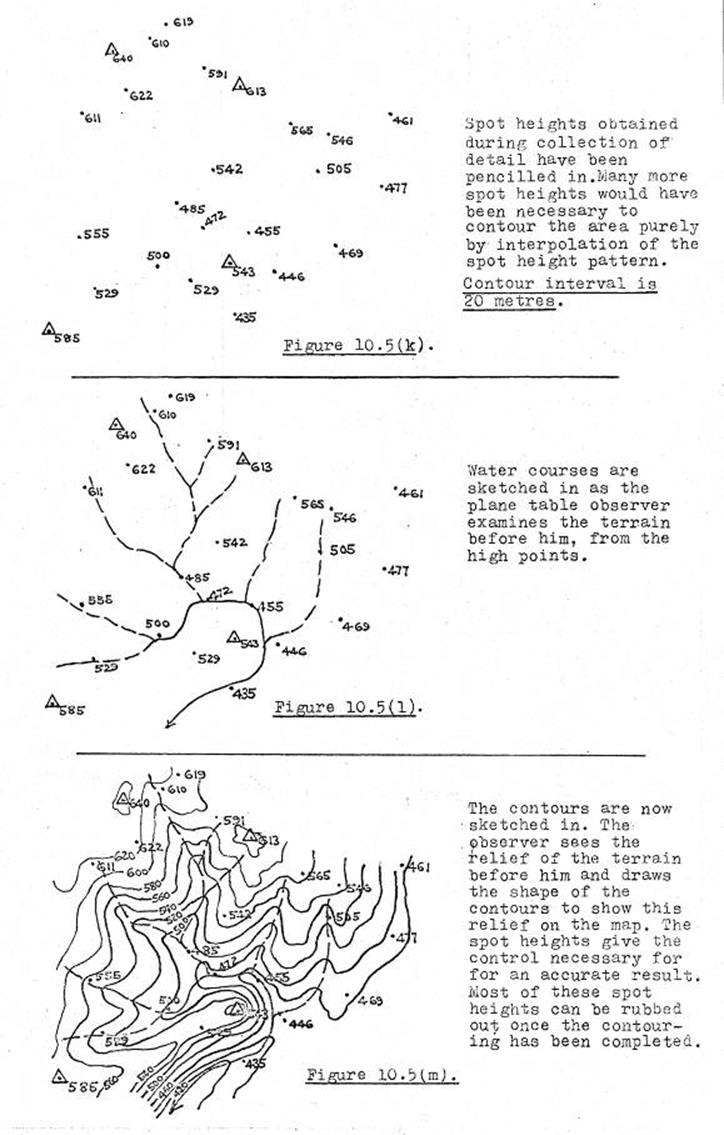
Practise is necessary, but the observer will soon start to imagine
each contour line running across the country side. Image a flood in the area,
gradually falling, and revealing the terrain to the observer as each contour
interval is reached. See notes in the Map Reading section 10.2(e): "How to
visualize relief from contours". In this case the plane table observer's
task is the reverse, i.e. "How to visualize contours from relief".
The methods of contouring described are illustrated in Figures 10.5(k), (l) and (m).
The "Inaccessible Base" or "Two Point" Resection
When only two plotted control points are visible from a point
whose position is required, a simple resection is impossible. The "inaccessible base" method can be used in this case. It has been included mainly for illustration of
survey principles rather than for general usage, the limiting factors being the
length of the base required and the distance this base is from the control points. (Draw a
few diagrams with the base, one quarter the length of the distance between the control points and with varying
distances between the base line and the control points. It will be seen just
how weak are the angles or "cuts" which establish the trial positions
of the control points).
Description of the Method:-
A & B are the plotted control points which are visible.
P is the point whose
position is required.
Choose a point Q as the other end of a base, PQ. The length of
this base need not be known but A & B must be visible from Q, and the base
would need to be at least ¼ the length of the distance
A to B.
Ignore the plotted points on the board.
A line pq is plotted at any convenient length, and A & B are intersected
from P & Q which are both visited. This gives a' & b' on the board and
also a figure pqb'a'
which is
mathematically similar to the figure PQBA in nature.
To set the board, the
alidade is placed along a'b', and some object, x is sighted. The alidade is
then placed along the plotted positions ab and the board is rotated until x is
again sighted. Thus the board has been rotated through the error of orientation
Ɵ, and is now correctly
set. Erase the surplus plotting.
The correct position of p is then obtained by pulling in rays from
A & B
through a
& b respectively.
Figures 10.5(n), (o), & (p) show the steps necessary to give
the board its correct orientation and thus ready to proceed with 5 above. In these notes and
in the diagrams, the capital letters, A, B, etc, refer to the positions in nature and the lower case,
a, b, etc refer to the
positions as plotted on the board.
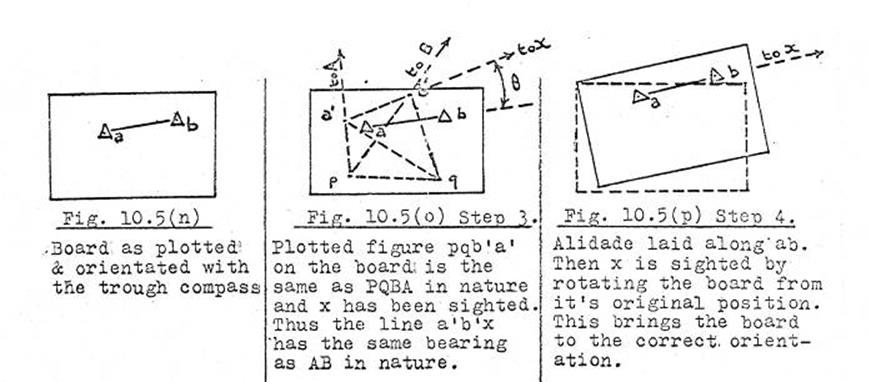
Finishing
This will depend on the requirements of any particular task;
normally the minimum necessary to be shown would be the area, scale, contour
interval, grid coordinates, the date and a magnetic north point.
It is important that the observer has clear instructions on all
the above as well as the type of detail which must be shown and what may be
omitted. For example, at some scales fences may not be shown at all, whereas at
others they are a very important part of the detail. Similarly at some scales only main gates in fences, are shown,
while at others it is important to show every gate.
11.
Elementary Algebra, Logarithms, Plane Geometry &
Trigonometry
Due to the complex formatting and possibility of error this
section, despite its slightly poor quality, is presented in PDF
format.
12 Survey
Computations
General
The
more basic of the field computations have already been dealt wlth.
These
were :
Reference
Marks Section 3.5
Eccentric
corrections Section 3.6
Tellurometer
measurements Section 4.3
In
this section it is proposed to deal with other computations, some of which will
be more of a background to survey work and others which will be regularly used.
12.1 Closed
surveys (chain & theodolite traverses)
Bearing are
specified on the Whole Circle or Azimuth method. In this method,
bearings originate from North (0° or 360°) and are
measured clockwise from the meridian through East (90°), South (180°),
West (270°) and back to North.
Bearings
of 0°, 90°, 180°, and 270° are
known as Cardinal Bearings.
To compute
the bearing of any line from the bearing of a reference line where the angle
between the reference line and the required line is known the procedure is :

Add
angle to bearing Subtract angle from bearing
Bearing
0->A = 37° 10’ 17.2” Bearing 0->A = 257° 41’
41.8”
Clockwise
angle + 107° 13’ 55.1” Clockwise angle - 101° 10’ 11.7”
Bearing
0->B = 144° 24’ 12.3” Bearing 0->B = 156° 31’
30.1”
If
the sum exceeds 360° subtract 360°. If the difference would be negative add
360° to the known bearing prior to the subtraction.
Latitude
and Departures
Any
line, except a cardinal line, can be resolved into two components :
A
North or South component and an East or West component.
A
cardinal line may only have a North or a South, or alternatively an East or a
West component.
The
North or South components are called Latitudes.
The
East or West components are called Departures.
If
there are two digits in the degrees and the figure is greater than 90°, drop
the 9.
Bearing
95°
58' = 5° 58’ Direction angle.
The
angles derived from these bearings is shown in the diagram, below :
Step
2 : Multiply length of line by sine and cosine of Direction angle.
The
products will be the Latitudes and Departures. But which product gives what
component? Draw the following diagram :
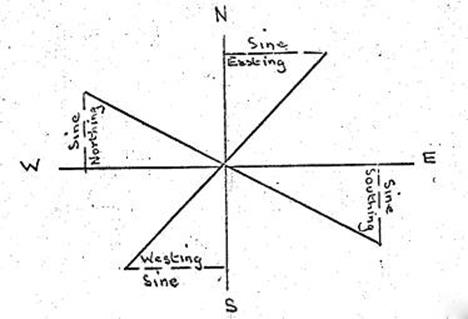
For
the first few times computations are performed draw this diagram and keep it
beside you. Multiply the distance by the sine first and enter the product in
the component column shown by the diagram. Now that the sine component is
settled in its column, and as there can only be one other component for the quadrant the
product of the length and the cosine of the direction will give it.
If
the length of the line and its azimuth or bearing are known, the latitudes and
departures can be determined easily by the rules trigonometry pertaining to
right angled triangles.
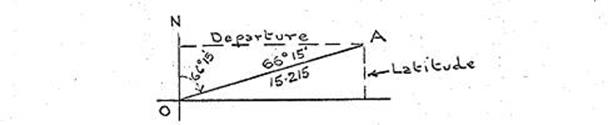
Departure
or Easting = 15.215 sin 66° 15' = 13.926
Latitude
or Northing = 15.215 cos 66° 15’ = 6.128
Put
in other words - a point starting at 0 and travelling to A, over a distance of
15.215 metres, on a bearing of 66° 15’ would travel in an easterly direction for
13.926 metres and in a northerly direction of 6.128 metres.
Where
using tables which give functions of angles from 0° to 360° :
Multiply
the sin bearing by the distance to get Departure or Easting;
Multipy
the cos bearing by the distance to get Latitude or Northing.
Where
using tables which give functions of angles between 0° and 90° only, the
following procedure is adopted.
Find
the direction angle for the given bearing :
The
direction angle is obtained by subtracting the cardinal bearing that is nearest
in an anticlockwise direction from the bearing of the line, thus :
Bearing 125°
16’
Nearest
anti-clockwise cardinal 90° 00’
Direction
angle
35° 16’
Bearing 323°
11' 35”
Nearest
anti-clockwise cardinal 270° 00' 00”
Direction
angle 58° 11’ 35”
Another
quick method :
Add
the first 2 digits of 3 digit degrees together, but leave the third digit
degrees and the minutes and seconds unchanged.
328°
11' 35” = 58° 11' 35° Direction angle.
If
the sum of the 2 first digits gives two digits add those 2 digits together
again.
297°
15' = 117° 15' = 27° 15' Direction angle.
Of
course, if there are only two digits in the degrees less than 90° the figures
need no alteration.
Bearing
87°
43’ 30" = 87° 43' 30” Direction angle.
Computing
closed surveys (Chain & theodolite traverses)
A
survey which starts at a point and is carried out by a succession of traverse
lines back to the starting point is known as a "closed survey". In
such a survey checks can be applied which will show the total accumulated error
in the work. These total errors are known as "miscloses".
Angular
Misclose
Suppose
ABCDE is a closed survey. AB is the azimuth line, bearing 84° 28' 30" and
at B, C, D and E the bearings of BC, CD, DE and EA are observed. If the
instrument is now set up at A and the bearing AB observed it should of course
read 84° 28' 30". As a matter of experience it will usually read
slightly higher or lower, say 84° 29' or 84° 28'. The discrepancy so observed is called
the angular misclose and is due to unavoidable errors in reading the angles.
Latitude
and Departure Misclose
If
a survey starts and finishes at A it is obvious that for every one metre which
it advances North or East it must advance one metre South or West. To compute
the latitude and departure misclose or "take out a close" the
Northing or Southing (latitude) and the Easting or Westing (departure) of each
line are computed and if they do not balances the discrepancy is known as the
misclose. This misclose is due to errors in both chaining and observing angles.
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
Length
|
North
|
South
|
East
|
West
|
|
AB
|
84° 28’ 30”
|
95.256
|
9.171
|
|
94.813
|
|
|
BC
|
172° 50’ 30”
|
36.600
|
|
36.315
|
4.516
|
|
|
CD
|
144° 29’ 30”
|
49.243
|
|
40.085
|
28.601
|
|
|
DE
|
259° 11’
|
61.067
|
|
11.460
|
|
59.982
|
|
EA
|
319° 11’
|
103.992
|
78.702
|
|
|
67.973
|
|
|
SUM
|
|
87.873
|
87.860
|
127.975
|
127.955
|
|
|
MISCLOSE
|
|
|
0.013
|
|
0.020
|
|
|
|
|
|
|
|
|
The
misclose is shown here as two components - the misclose in the Latitudes and
the misclose in the departures. It is always written under the lesser of the
figures.
Now
try this close for yourself by writing down the bearings and distances and
computing the latitudes and departures - of course keep the example out of
sight. If you get a shocking misclose in Latitudes or Departures the chances
are that you have placed a latitude or departure in the wrong column. Check the
positioning of the components as follows :
The
directions of the components in any quadrant are the directions of the cardinal
lines defining that quadrant, and the greater of the components is in the
direction of the nearer of those cardinals. For example, the bearing of the
fourth line is 259° 11' ie. it is between South and West and nearer to West so
its components are placed accordingly, the greater in the West column and the
lesser in the South column. If a line is cardinal of course it has only one
component, in the direction of its bearing, and the length of that component is
the length of the line.
After
this check you will have reduced the misclose considerably, however, an
unacceptable misclose may remain. This is probably due to :
Mistake
in looking up the trig functions
Mistake
in multiplication
Mistake
in writing down a product.
This
can be checked by repeating the whole operation, however, this is an
unsatisfactory method as the same mistake may be repeated. An independent check
on the multiplication can be obtained by using Gousinskys Tables.
These
tables list the difference between the sine and cosine of the Direction angle.
Use
them this way :
Look-up
the table value for the direction angle of the line
Multiply
this value by the length of the line
To
the product add the lesser of the two components obtained in the close.
The
sum should be within 0.001 of the value obtained previously for the larger
component. If not, check the previous multiplication. In 90% of the cases you
will find you have made mistakes (a), (b) or (c) above.
Now,
if a mistake still remains check the addition of the components. In 1% of cases
you will find a mistake.
If
a misclose still remains then check the bearings and distances entered.
If
after making all the checks listed above an unacceptable misclose still
remained on a practical job the bearing of the misclose would be computed and
the measurement of any line in the close near that bearing would be checked.
However, the misclose bearing may not be anywhere near one of the traverse
bearings in which case there may be mistakes in the measurement of more than
one line or an angular mistake that is not apparent due to compensating
blunders. Repetition of the work is required in such a case.
It
is important to realise that the misclose only shows the uncompensated errors.
This is particularly important in the case of chaining. It is often the
practice to neglect the corrections due to temperature, sag and tension or
rather to accept an approximate figure for the temperature and apply an
estimated tension based on experience, which should balance the sag and tension
corrections. Provided the estimated temperature is within 10° or so of the true
figure and reasonable judgment is used in applying the tension the resulting
errors should be well within the limits prescribed for boundary definition.
At
the same time errors from these sources will tend to be uniform so that those
made in Northerly or Easterly lines will tend to balance those made in
Southerly or Westerly lines and the error shown by the misclose will be
misleading.
Incomplete closes
The
principles of computing latitudes and departures can be applied to the computation
of missing bearings and distances. Computation by latitudes and departures of
missing bearings and distances is usually more efficient than by solving
triangles.
 Case 1 : Bearing and Distance of one line
missing
Case 1 : Bearing and Distance of one line
missing
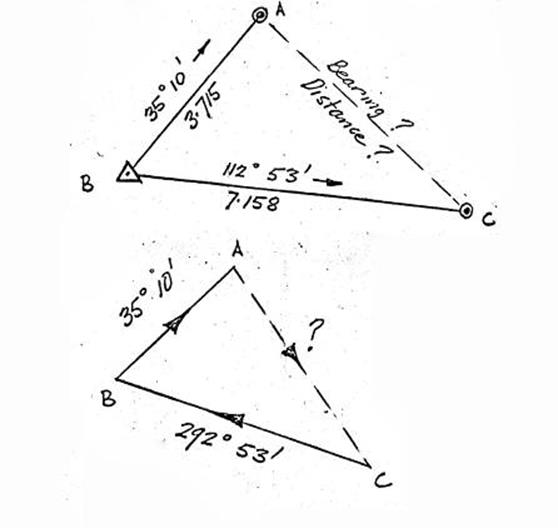
In the first sketch above we have an example of the information
normally obtained when surveying reference marks.
A
theodolite at B has determined the bearings of lines B to A and B to C and the
horizontal lengths of these lines have been determined. A to C remains to be
calculated.
The
first step is to write the bearings down so they will be travelling in the same
direction around the figure. If the bearing of A to C is required the bearings
for the close must follow on in the same direction as in the second sketch
above.
Bearing
B to A is already given in the correct sense and remains 35°10'.
Bearing C to B is the reverse of the bearing given (B to C). To maintain the
direction 180o must be added to bearing B to C (reverse the
bearing). This gives the bearing C to B of 292o 53'. The incomplete
close may now be stated, the latitudes and departures computed and the
"misclose” determined.
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
Length
|
North
|
South
|
East
|
West
|
|
CB
|
292° 53’
|
7.158
|
2.783
|
|
|
6.595
|
|
BA
|
35° 10’
|
3.715
|
3.037
|
|
2.140
|
|
|
|
SUM
|
|
5.820
|
0
|
2.140
|
6.595
|
|
|
MISCLOSE
|
|
|
5.820
|
4.455
|
|
The
“misclose” gives the latitude and departure of the missing line - the line
required to complete the close. We now know that the missing line has a
southing of 5.820 and an easting of 4.455 and consequently it must have a south
easterly bearing.
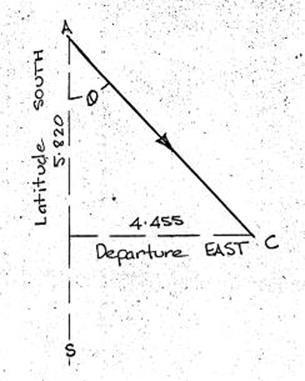
In
computing
the missing line the lesser of the two components should be divided by the
greater. The result is the tangent of the angle made with the nearest cardinal
line. The direction of that cardinal is the direction of the greater
component, and the side of that cardinal on which the missing line lies is
given by the direction of the lesser component.
Tan θ = 4.455 / 5.820 = 0.765 464
θ = 37° 26'
The greater component is a southing so the angle computed is
between the 180 cardinal and the missing line.
The lesser component is an easting so the missing line must lie to
the east of the 180 cardinal.
Bearing AC = 180° 00' — θ = 180° 00' – 37° 26’ = 142° 34'
The length of AC is computed by multiplying the greater component
by the secant of θ.
sec 37° 46' = 1.259 349
5.820 x 1.259 349 = 7.329 = AC
The completed calculation should look like this:
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
Length
|
North
|
South
|
East
|
West
|
|
CB
|
292° 53’
|
7.158
|
2.783
|
|
|
6.595
|
|
BA
|
35° 10’
|
3.715
|
3.037
|
|
2.140
|
|
|
|
SUM
|
|
5.820
|
0
|
2.140
|
6.595
|
|
|
MISCLOSE
|
|
|
(5.820)
|
(4.455)
|
|
|
AC
|
(142° 34’)
|
(7.329)
|
|
1.259349
|
0.765464
|
37° 26’
|
Note :
All
the quantities for the computed line (bearing, length, latitude and departure)
are bracketed to identify them from the quantities of the observed lines.
The
computed tangent angle and secant are written in the line below the misclose.
To
check the computation, three methods could be tried.
Check
all latitudes and departures with Gousinsky's Tables. This method will not
check the addition and subtraction of components but is usually quite
sufficient.
Solve
the plane triangle. Two sides and the included angle known.
Swing
the bearings by a constant amount. The best way is to add or subtract an angle
from the bearings so that the computed line would be cardinal.
Example Method (c)
If 37° 26' was added to the bearing of AC it would then be 180°.
Add 37° 26' to the observed bearings.
The close will now be.
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
Length
|
North
|
South
|
East
|
West
|
|
CB
|
330° 19’
|
7.158
|
6.218
|
|
|
3.545
|
|
BA
|
35° 10’
|
3.715
|
1.111
|
|
3.545
|
|
|
|
SUM
|
|
7.239
|
0
|
3.545
|
3.545
|
|
|
MISCLOSE
|
|
|
(7.239)
|
(0.0)
|
|
|
AC
|
(180° 00’)
|
(7.329)
|
|
|
|
|
AC now computes with a bearing of 180° 00' as planned and length
the same as computed previously.
All stages of the original computation have been proved by this check. However,
it must be remembered that although the mathematical operations have been
proved to be perfect any error that existed in the original data is thrown into
the computed line.
Case 2 : Two missing distances
Suppose
the lengths of AB and BC in the first close unknown. This case could arise
where B is an inacessible point, or if accessible, the distances, cannot be
measured.
Solution
:
Alter
the azimuth of the survey by adding to or subtracting from each bearing such an
angle as will make the bearing of one of the incomplete lines cardinal.
In
this case add 5° 31 30°. This will make AB cardinal. Compute the components of the
complete lines on this altered azimuth, tabulate them as before and find the
latitude and departure required to close the figure.
As
one of the missing lines is cardinal it will have no latitude or departure
according as it is east-west or north-south. It follows then that the latitude
or departure, as the case may be, which is required to close the figure must be
allocated to the other line. For this line we have its bearing and one
component from which its length and the other component can be computed as
sides of a right angled triangle.
These
figures are inserted in the table and the departure or latitude now required to
close the figure must be allocated to the remaining line, and is the length of
that line.
Draw
a diagram
approximately to scale, as above, to get a clear picture of the missing
distances and the calculations required.
See next page for method of laying out the work with each step
nominated.
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
New B’rng
|
Length
|
North
|
South
|
East
|
West
|
|
AB
|
84° 28’ 30
|
90° 00’
|
95.235
|
|
|
95.235
|
|
|
BC
|
172° 50’ 30”
|
178° 22’
|
36.610
|
|
36.595
|
1.043
|
|
|
CD
|
144° 29’ 30”
|
150° 01’
|
49.243
|
|
42.653
|
24.609
|
|
|
DE
|
259° 11’
|
264° 42’ 30”
|
61.067
|
|
5.632
|
|
60.807
|
|
EA
|
319° 11’
|
324° 42’ 30”
|
103.992
|
84.880
|
|
|
60.080
|
|
|
|
|
|
84.880
|
48.285
|
25.652
|
120.887
|
|
|
|
|
|
-48.285
|
|
|
-25.652
|
|
|
|
|
|
36.595
|
|
|
95.235
|
Step 1 : For BC subtract South from North to get complement
(36.595) for line.
Step 2 : From South complement and bearing of line get length BC
(36.595 sec 1°38’ = 36.610) and enter in length column.
Step 3 : From length BC and bearing compute departure East
(1.043).
Step 4 : Total East and subtract from West to get East for AB
(95.235) and length of AB.
To check recomputed on original bearings. The figure must close or
the computations are wrong.
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
Length
|
North
|
South
|
East
|
West
|
|
AB
|
84° 28’ 30”
|
95.235
|
9.169
|
|
94.792
|
|
|
BC
|
172° 50’ 30”
|
36.610
|
|
36.325
|
4.562
|
|
|
CD
|
144° 29’ 30”
|
49.243
|
|
40.085
|
28.601
|
|
|
DE
|
259° 11’
|
61.067
|
|
11.460
|
|
59.982
|
|
EA
|
319° 11’
|
103.992
|
78.701
|
|
|
67.973
|
|
|
|
|
87.870
|
87.870
|
127.955
|
127.955
|
A
misclose of 0.001m would be permissible. This would occur from the errors
introduced when the decimals of the components are rounded off. By computing an
extra decimal place in both closes, the rounded off latitudes and departures
could be made to close.
Again
the assumption must be made that the measured lines have no error. Any unknown error
is thrown into the computed lines.
An
alternative method of solution is to find the length and bearing of the line
equivalent to the known lines, as previously described. By substituting this
equivalent for those known lines we obtain a triangle whose three angles are known as
well as the length of one side (as so computed). This solution is to be
preferred in the case of a close containing a great number of lines whose
components may have already been worked out. The former method is particularly
suitable when there are few lines.
Case
3 : Length of one line and bearing of another unknown
This
case is solved in a similar manner to the second case. The azimuth is altered
to make the bearing of the line whose length is missing, cardinal; and the
computation proceeds as before until the latitudes and departures of the known
lines are found, as shown :
The length of the line AB, and the bearing of the line BC are
required.
|
Line
|
Latitudes
|
Departures
|
|
|
Bearing
|
New B’rng
|
Length
|
North
|
South
|
East
|
West
|
|
AB
|
70° 10’
|
90° 00’
|
(156.088)
|
|
|
(156.088)
|
|
|
BC
|
(206° 33’)
|
(226° 23’)
|
124.968
|
|
(86.208)
|
|
(90.473)
|
|
CD
|
274° 56’
|
294° 46’
|
97.536
|
40.860
|
|
|
88.565
|
|
DE
|
305° 20’
|
325° 10’
|
33.528
|
27.520
|
|
|
19.151
|
|
EA
|
47° 13’
|
67° 03’
|
45.720
|
17.828
|
|
|
|
|
|
|
|
|
86.208
|
|
42.101
|
198.189
|
|
|
|
|
|
|
(86.208)
|
(156.088)
|
|
The latitude of the line BC is found to be 86.203, and its length
was given as 124.963. From the figure and calculation below it can be seen that two
bearings could give this south latitude, i.e.,
A line 46° 23' east of the 180° cardinal line, or
A line 46° 23' west of the 180° cardinal line.
In other words an ambiguous case
In
practice
there
should be no doubt as to which of these bearings is to be adopted. If there is,
further
information should be obtained such as an approximate length of the line AB,
or an approximate bearing of the line BC.
From the sketch it can be seen that BC will have a south-westerly
bearing. Therefore the bearing will be :
180° + 46° 23' = 226° 23'
This
bearing is entered in the “New Bearing" column, and the departure for that
line, computed. In this case West 90.473. The difference in departures gives the
missing length.
The
computed bearing is now converted to the original azimuth, and the computation is checked by
closing the figure on that original azimuth. This case can also be solved by
computing a closing line, AC, and solving the triangle ABC (two sides and the
non-included angle.)
Case
4 : The bearings of two lines missing
In
this case the solution is found by finding the bearing and length of the line
equivalent to the complete lines, and solving a triangle whose sides are this
line, and the two incomplete lines, to find the angles.
This case occurs
in practice when two circles intersect and it is required to find the bearings of their
radii from the point of intersection.
Note
:
In
all these cases care should be taken to avoid condtions which will give
unsatisfactory results. In the second case, the solution is unsatisfactory if
the lines are of nearly the same bearing when it will be found that the
cosecant and cotangent of a very small angle will be involved.
The
solution is similarly unsatisfactory in the third case when
lines are nearly at right angles, and in the fourth case when the sum of the
lengths of the incomplete lines is nearly equal to the length of the line
equivalent to the balance of the traverse.
Use
of Eastings and Northings instead of Latitudes and Departures
In
most of the computations of rectangular co-ordinates for mapping purposes,
Eastings and Northings only are used, and what has been designated as a Departure of
East becomes +East, and a Departure of West becomes -East; a Latitude of North
becomes +North and a Latitude of South becomes -North.
Thus,
with the use of full circle bearings also, the system is very easy to grasp,
and the formulae simple.
Sine
bearing x distance = Diff. Easting, always.
Cos
bearing x distance = Diff. Northing, always.
The
signs of the DE and DN are easy to follow from this quadrant diagram :
0°
-E | +E
+N | +N
|
270°_______ |________
90°
|
-E | +E
-N | -N
|
180°
The problem in 12.1(c) would appear as follows under this system :
|
Line
|
|
|
|
Bearing
|
Length
|
Diff. Eastings
|
Diff. Northings
|
|
AB
|
84° 28’ 30”
|
95.256
|
94.813
|
9.171
|
|
BC
|
172° 50’ 30”
|
36.600
|
4.516
|
-36.315
|
|
CD
|
144° 29’ 30”
|
49.243
|
28.601
|
-40.085
|
|
DE
|
259° 11’
|
61.067
|
-59.982
|
-11.460
|
|
EA
|
319° 11’
|
103.992
|
-67.973
|
78.702
|
|
|
MISCLOSE
|
|
0.020
|
0.013
|
While
it is necessary to understand the use of Latitudes and Departures the simple
transition to the above method should be thoroughly grasped as it will be one
of the most used in mapping computations.
 12.2 Spherical Excess,
Closure of Triangles
12.2 Spherical Excess,
Closure of Triangles
In
Geodetic Triangulation, the triangles or polygons may, for all practical
purposes, be taken as spherical, and the sum of the angles exceeds that of the
corresponding plane figure by an amount termed "spherical excess",
(є).
Roughly,
spherical excess is 1" for every 197 square kilometres (76 square miles).
For
the terrestrial spheroid, the excess for a given area varies with the Latitude,
decreasing
from the Equator to the Poles. In this context the following terms should be understood :
"ρ"
: The
radius of Curvature in the Meridian.
Is
a measure of spheroidal, or arc distance. It is used to convert linear distance
along the meridian into terms of arc (Latitude differences).
"ν"
: The radius of Curvature Perpendicular to the Meridian, or in the Prime
Vertical.
Is
a measure of spheroidal or arc distance, where such distances are at right
angles to the meridian - that is, when converting Longitudes.
"ρ"
and "ν"
are both functions of the latitude of that place, and hence vary for different
latitudes. Geodetic Tables generally give values for them in the form :
1 , 1 or 1
etc.
ρ
sin 1" ν sin 1" 2ρν sin
1"
For
computing spherical excess, the term 1/2ρν sin 1" is used. This is explained in 12.2.1.
12.2.1. Formulae :
Spherical Excess = Area of triangle / R2 where R =
radius of a sphere.
When
the spheroidal shape of the Earth is used, R2 becomes ρν thus in the
term 1/2ρν sin 1" they are combined with sin 1" to bring
the value to seconds, and ½ from the formula :
Area of a triangle = ½ab sin C.
Natural values for 1/2ρν sin 1" for all latitudes
are tabulated as m x 10-8 in the Army Map Service Tables of Latitude
Functions (A.N.Spheroid).
Thus the formula becomes :
Є = ab sin C (1/2ρν sin 1")
where a & b are the two sides of the triangle, C the included angle, and
1/2ρν sin 1” is the function for the Mid-Latitude of the triangle.
12.2.2. Closing of
triangles
Although
the system of triangulation is now rarely used for the determining of distance
there still may be some call for the closing of triangles when laying
down mapping control. Also the calculation of spherical excess, the
closing of triangles and reducing spherical angles to plane angles helps the
understanding of many geodetic computations.
Figures
:
Simple
Triangles
: If
the observations were absolutely accurate the amount their total exceeds 180° would be the
exact amount of spherical excess in the triangle.
Quadrilaterals
: These yield 4 triangles as shown in Figure 12.2.2.(b). The total spherical
excess in each pair of diagonally opposite triangles equals the total of the
other pair. Thus immediate check of the arithmetic in totaling the observed
angles and calculating the spherical excess is available.
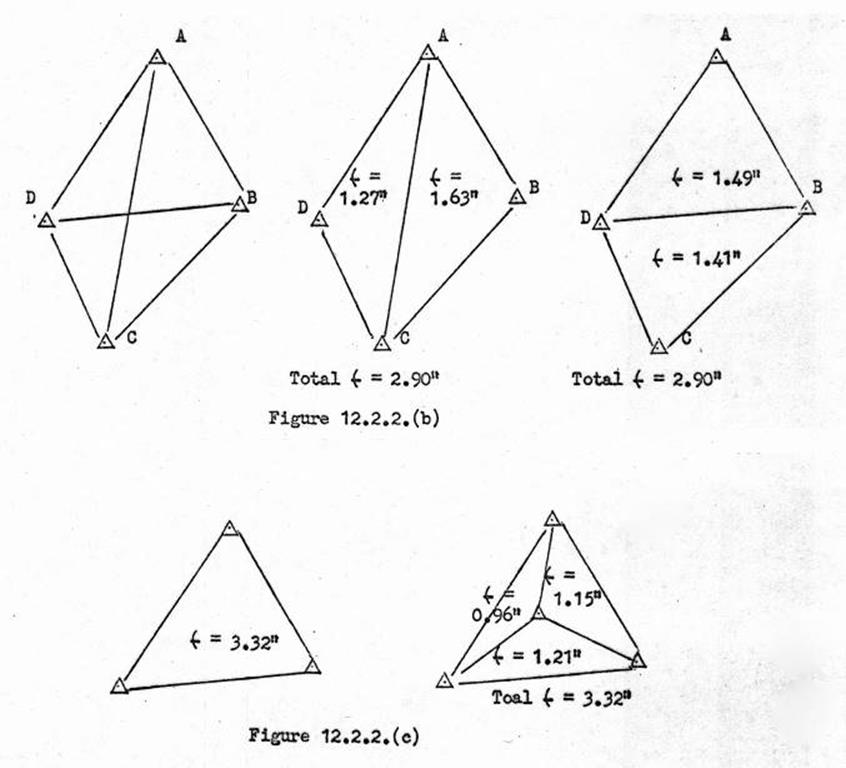
Centre
Point Triangles : The total spherical excess in the three included angles
equals that of the larger triangle. Figure 12.2.2.(c).

Calculation
of sides of triangles and spherical excess (Field Computation)
A
good layout for the above calculation is shown in Figure 12.2.2.(d). The
example is of a calculation using logarithms, but the same layout for the
angular data is suitable for natural calculations, the answers just being
entered in the appropriate column as they come from the machine.
Sequence
for calculating the sides :
Enter
observed angles and station names in their appropriate columns; lay out the
work so that the known distance goes on line three, as shown. Immediately above
it (on line two) enter the angle at the station opposite this known distance.
Total
the observed angles in each triangle.
Arbitarily
adjust the triangles to total 180° and enter these angles in the “Approx plane
angle" column. Nearest second will do.
The
sine formula is used and the log cosec. of the appropriate angle is used,
where necessary, to make the calculation a simple addition. Fill in the logs of the angles and the known
distance in the "Log Plane Angle" column.
Total
lines, 1, 2 & 3, as indicated to yield one side of the triangle and 2,3, &
4 to yield the final side.
Solve
all triangles in the same manner, using a calculated distance where necessary.
Some distances are calculated in different triangles; in these cases minor
differences in the last figures of the logs will occur.
Sequence
for calculating spherical excess :
The
spherical excess for each triangle is calculated twice as a check.
The
Mid-Latitude for the figure is scaled from the 1:250,000 scale map.
The
natural value for 1/2ρν sin 1" in this latitude, is obtained from the
A.M.S.Tables. Turn this into a logarithm if the calculation is to be in that
form.
Enter
this figure on line one in each of the (є) Excess columns. Below these
figures enter the log values for two sides and log sine of the included angle.
Total each column and they should yield the same answer for the spherical
excess of that triangle. Use three decimal places in the answer.
Round
off the spherical excess to two places and find the misclosure of all the triangles
in the figure.
Check
to see that the sum of the spherical excess of the diagonally opposite
triangles equals the other pair. Note that the same applies to the amount the observations
exceed 180° and also the algebraic sun of the misclosure of the triangles.
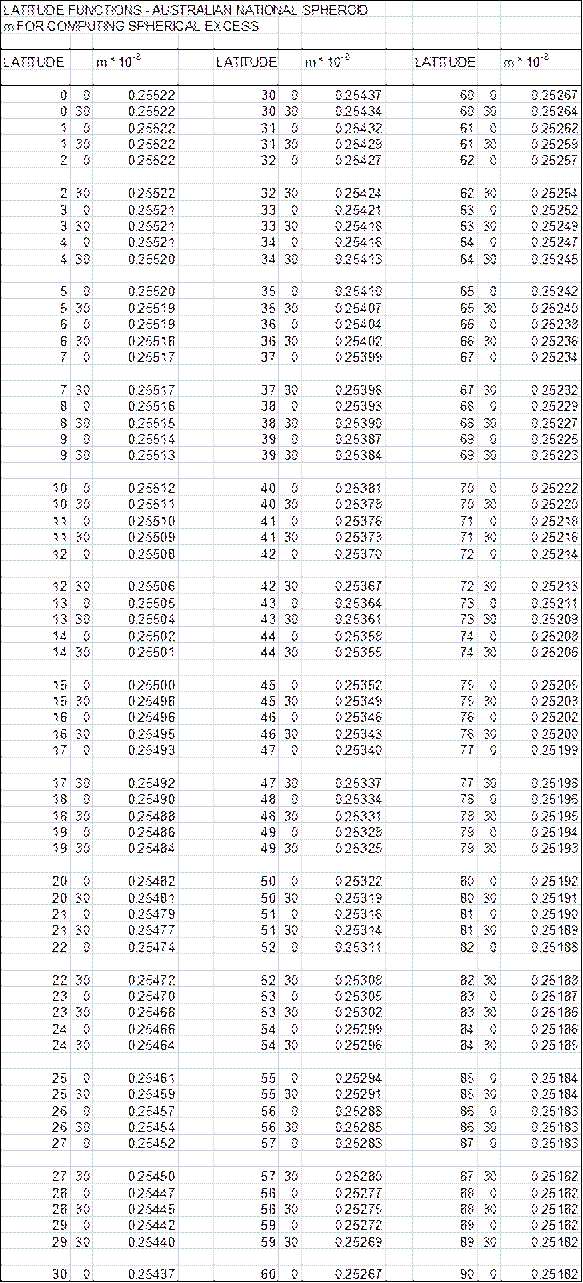
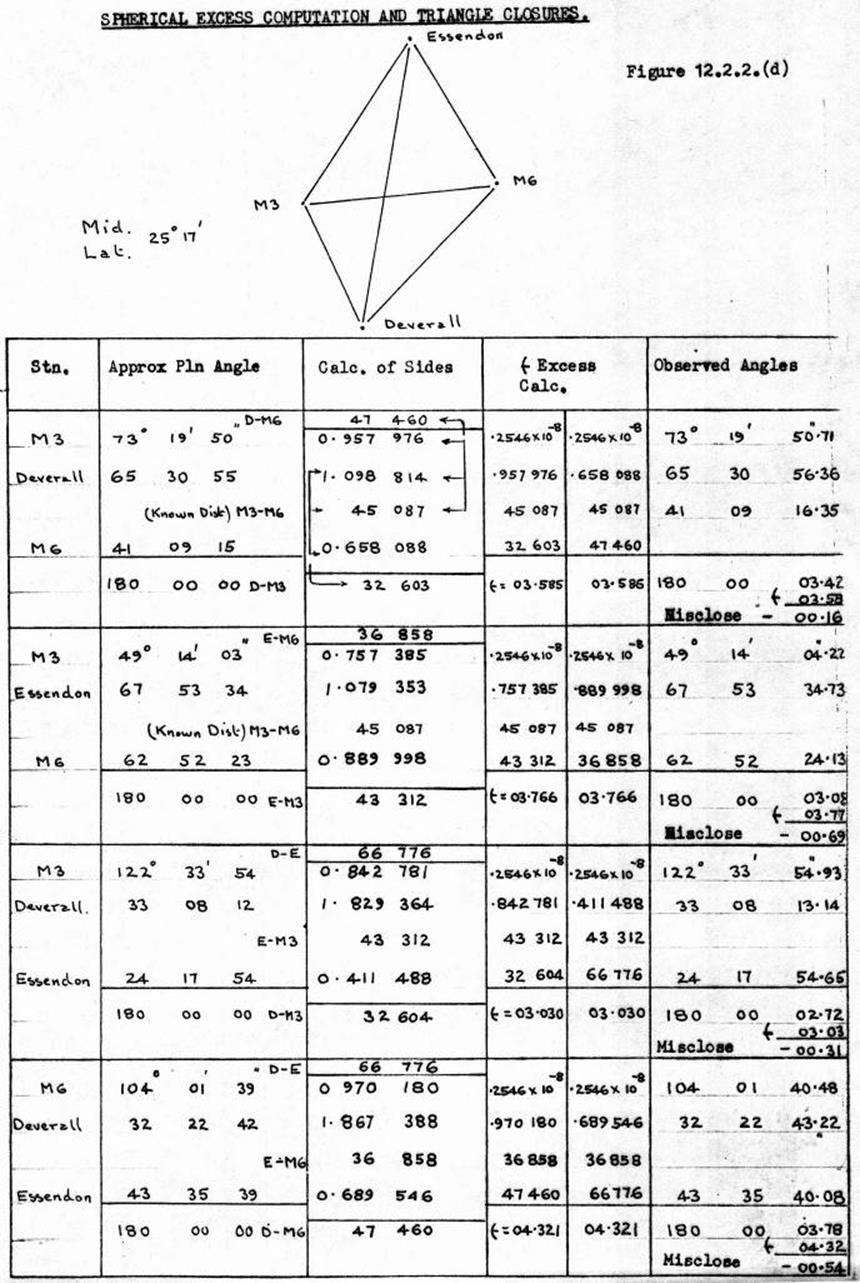
12.3 Field Computation : Latitude, Longitude and Reverse Azimuth
Definitions :
Bearings and spherical angles
The difference between 2 true bearings, from any given point, is a spherical
angle.
The observed angle between 2 points is a spherical angle (uncorrected for
observing errors).
True bearings with approximate spheroidal distances (S) are used
to calculate the Geographical Co-ordinates.
Distance S :
This
is the slops distance, station mark to station mark, approximately corrected to
Sea Level distance. The best available mean height for the line as taken from the map is
used for the Sea Level correction, but the minor corrections for slope and
Chord to Arc are disregarded.
Gauss Mid Latitude formulae :
The following formulae are satisfactory in field computations for
lines of lengths likely to be met with when measuring in Australia. However,
the formulae
are not completely accurate for lines over 30 kilometres and are not used in
the accurate office computations for lines longer than that distance.
Diff Latitude = Distance (s) cos Mid-Azimuth
(Zm) / ρ sin1”
Diff Longitude = Distance (s) sin Mid-Azimuth (Zm)
sec Mid-Lat / ν sin1”
Diff Azimuth (Z) = Diff Longitude x sine
Mid-Latitude.
where, as defined in 12.2. ρ sin1” and ν sin1” are Radii of
Curvature along the Meridian and perpendicular to the Meridian,
respectively.
See attached tables and example on the Field Computation proforma.
Note that South Latitude and East Longitude are taken as being positive in this
computation.
Sequence of computation :
Tabulate
the Back Azimuth at the known station, add the observed angle and obtain
Forward Azimuth. Tabulate Latitude and Longitude of the known station, mean
altitude of known and new station, and distance between these stations. Note which quadrant
the Forward Azimuth lies in and adopt the signs necessary from the sign
convention panel at the bottom of the proforma.
Find
the first approximate Mid Latitude using the data from the "M"
Correction of Latitude Table, the Latitude of the known station, Forward Azimuth and
distance to the nearest kilometre. The "M" table is listed for every
10° of Azimuth in each quadrant, using as a basis lines 10km long. For a
line xkm long the correction to Latitude is found by multiplying the correction
in the table by xkm/10.
To
find the approximate Mid-Azimuth :
Look
up the "K" factor for the approximate Mid Latitude.
Diff
Z = S
sine
Za *K
Where
: Za is the Azimuth at the known station.
K is the factor from the table.
S is the distance reduced approximately to Sea Level.
Halving
the difference Z and applying, with the correct sign, to the known azimuth will
give the approximate mid-Azimuth (Zm).
Computation
of the Final Values :
Using
Cos Zm in the Latitude formula will give Diff. Latitude and thus Latitude of
the New Station. Also an accurate Mid-Latitude.
Using
Sine Zm and Sec. of the accurate Mid-Latitude in the Longitude formula will
give Diff. Longitude and thus the Longitude of the New Station.
Finally,
this Diff. Longitude multiplied by Sine Mid-Latitude will give Diff. Azimuth,
which with the Forward Azimuth,+ or - 180°, will give the Azimuth
New Station to Known Station.
This
result of Diff. Azimuth for lines up to 30km in these latitudes should be
correct to within about 1" of the approximate result using the "K"
factor.
As
a final approximate graphic check, accurately plot the Known Station by
Latitude and Longitude on the 1:250,000 map. Plot the position of the New
Station by bearing and distance. Scale off its Latitude and Longitude; compare
with the calculated values and check for gross error by the map detail.
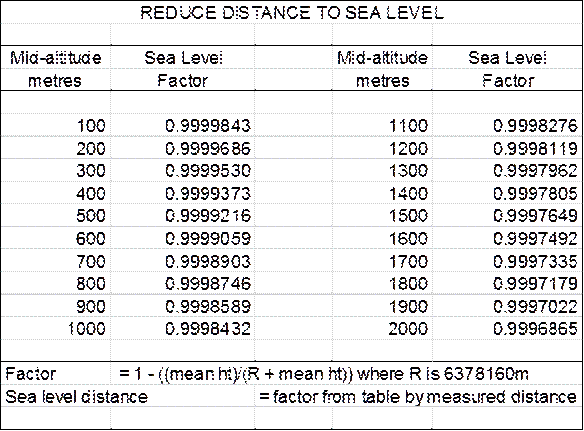

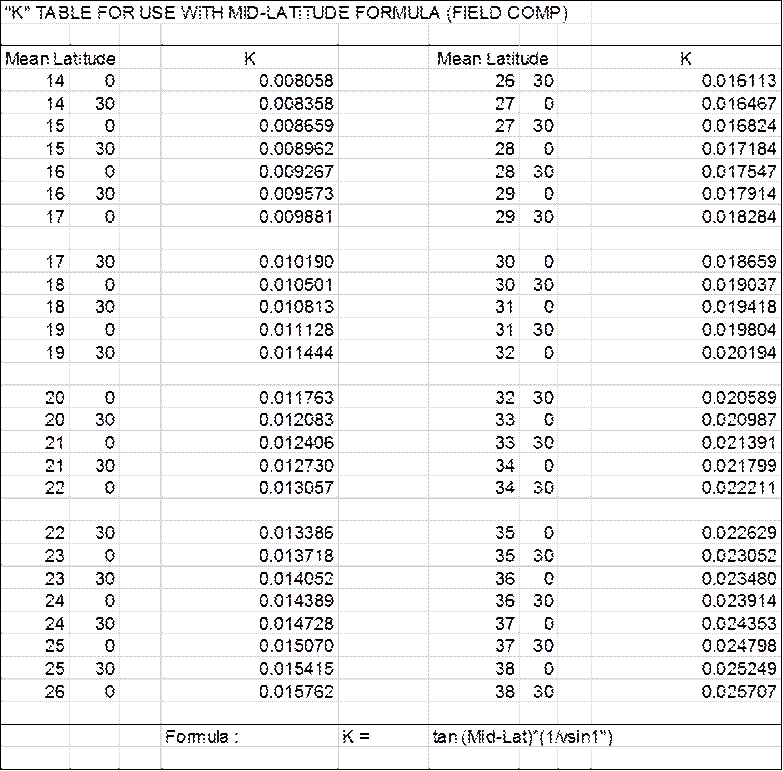

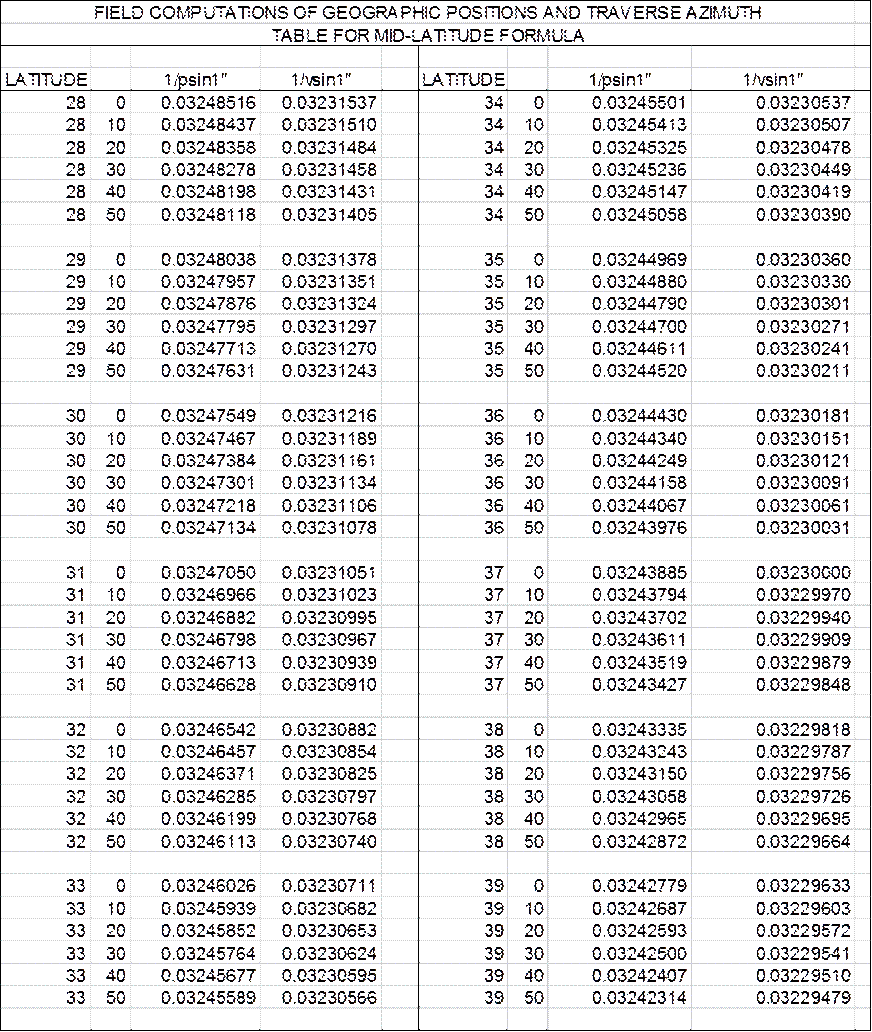
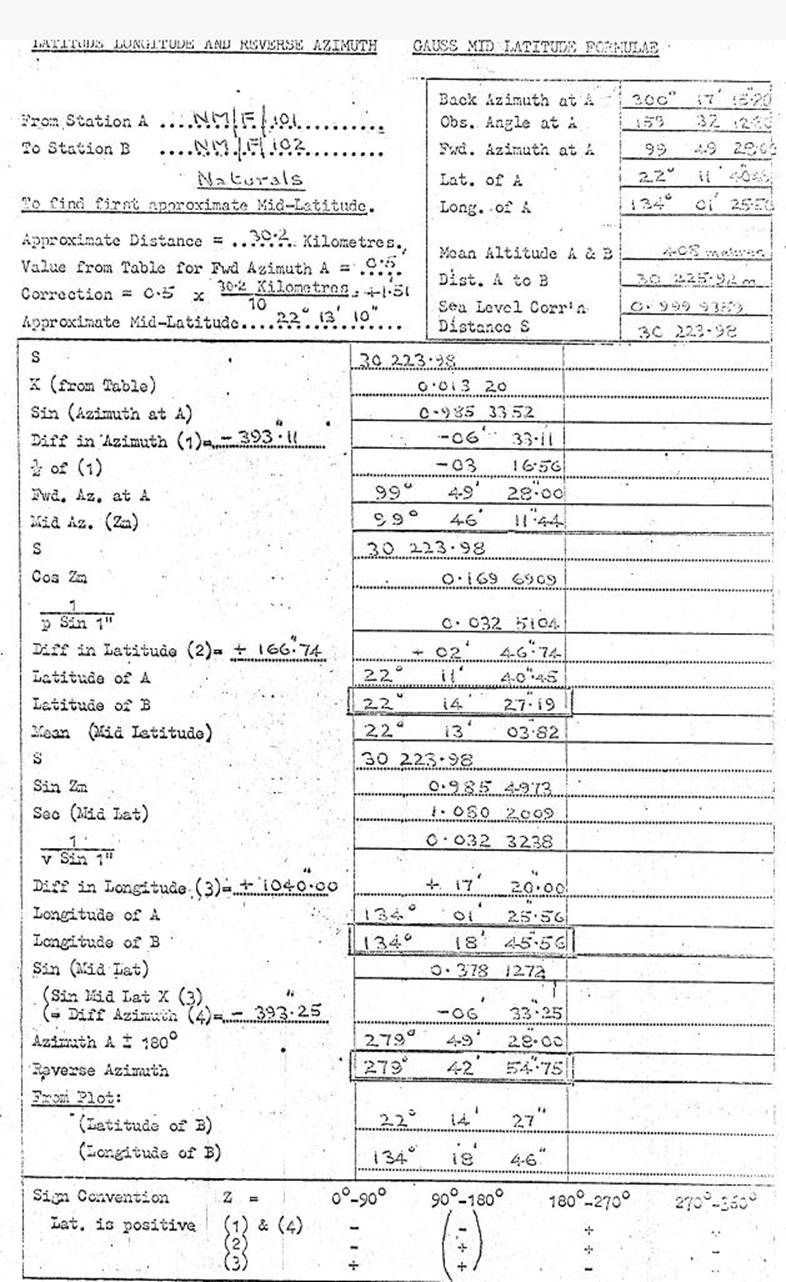


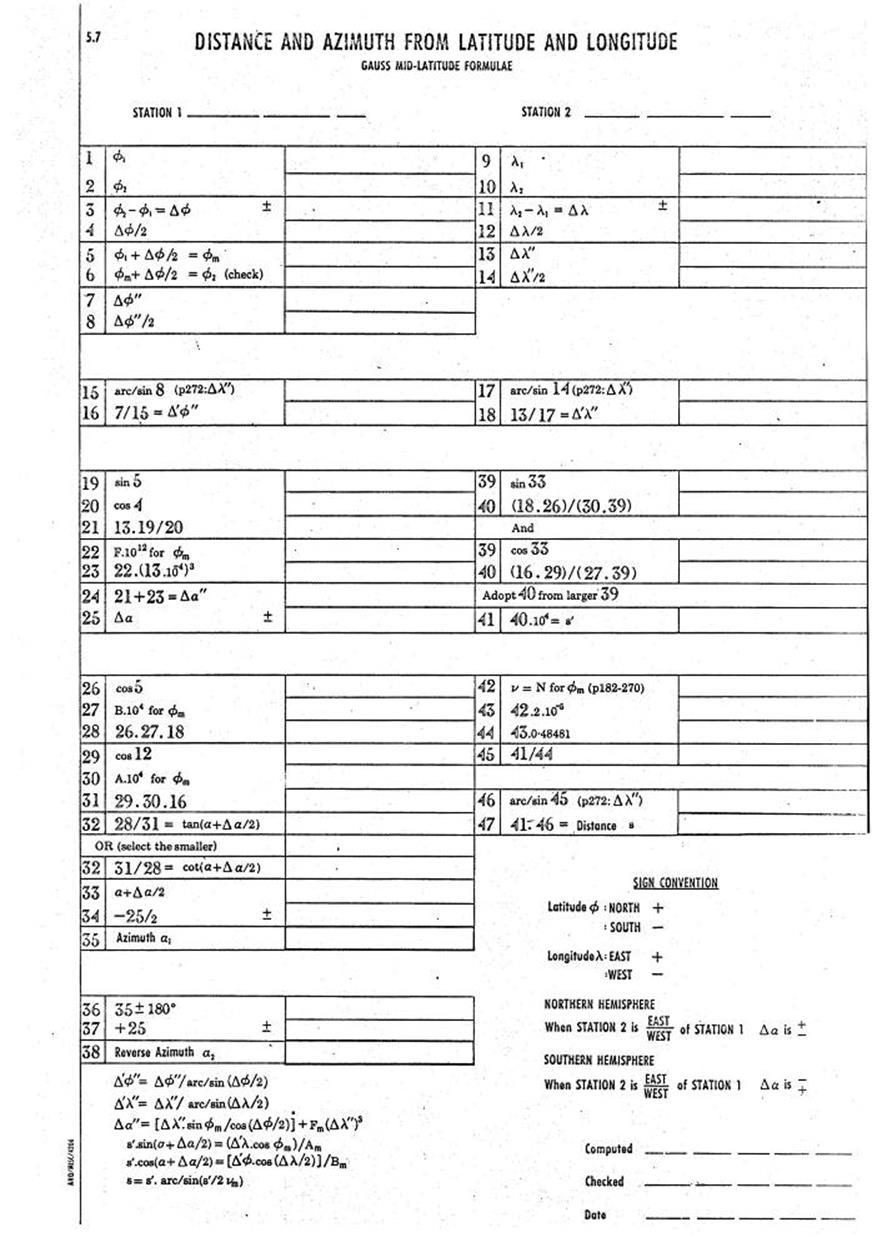
12.4 Heights from Simultaneous Reciprocal Vertical Angles
12.4.1 General
(i)
Included,
is a short explanation of the method of obtaining a Curvature and Refraction
index from Simultaneous Reciprocal (S.R.) Vertical Angular Observations, and
applying this index to a single ended vertical angle observation made
immediately prior to, or following, the S.R observation.
(ii) The height of an object
such as the side wall of a building can be obtained by reading a vertical angle
with a theodolite, measuring the height of the axis of the instrument above
ground level, and chaining the distance to the base of the wall.
Figure 12.4 shows such a simple problem:-
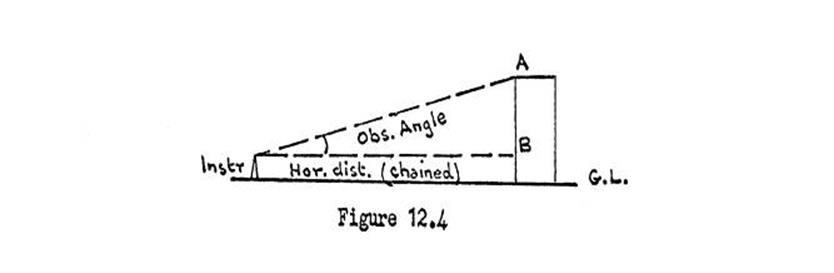
The Tan formula is used and from the diagram:-
AB = Horizontal Distance x Tan vertical angle
AB + height of instrument = Height of wall
While the above is the basis for calculating heights of
intervisible Mapping Control Points along a second order, or similar, traverse,
other factors prevent the problem being so simple.
(a)
Curvature
of the Earth
This curvature makes a distant object appear lower than it really
is:-
Curvature = (Distance between the two points)2 /Radius
of the Earth
Thus, curvature increases proportionately to the square of the
distance. The correction
is always
positive.
(b)
Vertical
Refraction
The influence of vertical refraction is not always the same, but
variable, depending on air pressure, temperature, humidity, force of wind,
vegetation, time of day, and even time of the year.
On a large plain the phenomenon of seeing a distant range some
hundreds of miles away during unusual atmospheric conditions, is often noted
soon after dawn or possibly just before dust.
The correction for refraction, can, for practical purposes be
taken as always minus. Where Curvature and Refraction is used, these
corrections are usually combined and the sum is practically always positive;
the influence of Refraction is only about 1/7 that of Curvature.
The inability to accurately determine vertical refraction is the
main difficulty in ascertaining heights by observing vertical angles. However,
by observing Simultaneous Reciprocal Vertical Angles, along each line,
refraction is cancelled out.
Good results can be obtained by adopting the further refinement of always observing
these Simultaneous Reciprocal angles at a time of day when the air is most
evenly heated
(i.e., not
before about 2 hours after the sun has crossed the meridian in that area, and not later than about 4 to 4½ hours after the sun
crossed the meridian.
It can also be mentioned at this point, that if a non-simultaneous vertical angle were read
to an unoccupied station immediately prior to, or following the simultaneous reciprocal observations a value for the Curvature and
Refraction Index obtained from the S.R. observation can be used in the
calculation of the non-simultaneous observation to give a fairly good result.
(c)
Instrument and Target Corrections
As shown in Figure 12.4 the height of the instrument axis is necessary
to obtain the height of the wall. In actual vertical angle observations, the top of the distant hill is
too indistinct to provide a clear laying mark so a target such as a heliograph, daylight lamp or
beacon vanes, is always provided. Thus the correction when observing S.R.
vertical angles involves two instruments and two targets along the lines shown in Figure 12.4(c).
Instrument and Target Correction = (Instrument A – Instrument B + Target A –
Target B) / 2
12.4.1 Computation of Heights
from Simultaneous Reciprocal Vertical Angles
Formula :
Figure 12.4.1 shows 2 hills on the earth's surface, how the plumb
line from each station would converge and finally meet at the centre of the
earth, also how the level plane at each station would appear. This shows why
vertical angles
at intervisible
stations are usually angles of depression.
The following simplified
formula, although not perfectly accurate is sufficiently so for computing most
difference heights from vertical angles.
Explanations of formulae
are outlined in Clarke Vol. 2 "Difference of Elevation from Reciprocal
Observations."
Diff. Height = Distance
between stations A & B x Tan½
(Angle at A -
Angle at B) (Taking
signs of observed angles into
account)
In the above formula, two or the approximations are :
In the small vertical
angles normally involved, the sines and tans of the angles are the same (to 6 places of logs.).
With these small angles the slope distance and horizontal distance
are so similar that no inaccuracy is introduced by using the Tan and distance between stations as measured by a
tellurometer.
If there is considerable
difference in height between stations the problem can be resolved by:-
Using the Slope distance
& sine of the vertical angle.
Compute the approximate
heights using Tan; correct the slope distance to horizontal distance, then
recompute the heights with this accurate horizontal distance.
Distances should not be
reduced to sea level for height computations.
Components of Vertical
Angular Observation
Referring again to Figure
12.4.1, and giving thought to the problem it will be realized:-
All vertical angles have an Elevation or Depression component, a
Curvature component, and a Refraction component. The last two, in all the
following explanations, will be combined as the "C&R" component.
If both Vertical Angles from 2 intervisible stations are of
depression, the angle of least depression is made up of an elevation component
(+) and a C&R component (-), and was
observed from the lowest station.
 The angle of most depression is made up of a
depression component (-) and a C & R component (-), and was observed from the highest station.
The angle of most depression is made up of a
depression component (-) and a C & R component (-), and was observed from the highest station.
Examine the observed
vertical angles from two intervisible stations along these lines:-
Station A (Depression) 00°'11¢ 47.2"
This is the Elevation angle.
Station B (Depression) 00° 14' 19.4" This is the Depression
angle
From the above it can be seen that if Station A is the station of
known height, the sign of the true vertical angle (when C&R are eliminated)
will be Elevation, thus the difference height will be plus.
To avoid having to examine
each pair of vertical angles along these lines the following can be adopted:-
At the station with the known height:
Elevation angles are + & Depression angles are - i.e. signs as
observed.
At the station of which ht
is required: Elevation angles are - & Depression angles are + i.e.
change signs.
From this:-
Station A (Known Height) Depression
angle - 00°
01' 47"
Station B (Height
Required) Depression angle +00° 14¢ 19²
2 ) +00° 12¢ 32²
Vertical Angle A to B +00° 06¢ 16²
It can now easily be seen how
the C & R can be obtained from these figures and also the various
components of both observed angles:-
Stn A to B Stn
B to A
Vertical angle component
(True angle) +00°
06' 16" -00°
06 16"
Curvature & Refraction
component - 00°
08¢ 03² -00° 08¢ 03²
Observed vertical angle -
00° 01¢ 47² -00° 14¢ 19²
12.4.2 Sequence of Calculation using
proforma (Logs or Machine)
Data Section
Enter heights of instruments
and signals at each station, total and carry result to appropriate line in the
calculation section.
Reciprocal Ray Section
Enter the observed vertical angles; for clarity and future
checking it is a
good idea to
mark the elevation angles "E" and the depression angles "D"
instead of + or -. Now give each angle the signs indicated; this really amounts
to changing the signs of one angle as mentioned in 12.4.1, section (iii). Sum, algebraically and
reduce to seconds.
Calculation.
Logs. Log the seconds,
log the distance between stations.
Sum of these with the constant for log tan 1² gives difference height. Apply diff. height, instrument and
signal corrections to known height of the station to obtain height of distant
station.
Machine. The vertical angle
in seconds x distance x tan 1" = difference height. Enter the result in
the appropriate column and apply with instrument and signal corrections to
known height of the station to obtain height of distant station. See Figure 12.4.2 for an example
computation.
12.4.3 Calculation
of a Single Ray Height using C&R Index from S.R. Vertical Observation
As mentioned in 12.4(b), if a single ray vertical angle is
observed to an unoccupied station immediately prior to, or following, the
observation of simultaneous reciprocal vertical angles, a "C&R
Index" can be calculated
from the S.R. vertical angles and applied to the single ray to give fairly good
results. Reasonably stable weather, and observations at the best time of the day, as previously
mentioned, are necessary. Also the correct distance between the stations.
Briefly the calculation involves finding the Curvature &
Refraction component of the observed angle as shown in 12.4.1, section (iii).
This value needs adjusting by the algebraic sum of the instrument
and signal corrections converted to seconds. This time both instruments are plus corrections, and both signal
corrections are minus corrections. The full amount of Curvature & Refraction, in seconds, is
divided by
the distance between stations to produce the C&R Index.
For calculating the single ray, the C&R Index x distance gives
C &R in seconds, along that ray. This is applied, algebraically, to the
observed angle to give the correct vertical angle between the stations. Thus,
the difference height is calculated, the instrument height at the observing station and the signal height at the
distant station, are the only other corrections to apply.
12.4.4
Sequence of calculation using the proforma (Logs or Machine)
Calculation of C&R
Index:‑
Enter instrument and
signal heights of S.R. vertical angle ray. Sum, algebraically.
Logs. The log
instrument & signal correction + log cosec 1" + colog distance between
stations gives
instrument
& signal correction; in seconds.
Machine. Instrument
& signal correction (seconds) = Instrument & signal correction *
cosec 1"
Distance between stations
Enter S.R. observed vertical angles; this time signs are as the
angles were observed. Sum and halve to get the amount of Curvature & Refraction in
the angular observation. Convert to seconds, apply instrument and signal
correction to get C&R in seconds, along the line.
The C & R divided by the distance between stations gives a
C&R Index.
Calculation of single ray using the C&R Index (Logs or Machine)
In the computation of height section, enter:-
Height of instrument at the observing, station, height of signal
at the distant station. Sum algebraically, and enter result in the appropriate
column. As one observer only, is involved, do not divide by two in this computation.
Enter the observed angle
in the correct column; single ray section.
Logs. Log distance
between station + log C&R Index gives Curvature & Refraction along the
ray in seconds. Enter this below the observed vertical angle. The algebraic sum of these gives the
vertical angle along the ray.
Machine. Distance x
C&R Index gives the same result; enter, and proceed as explained in (ii),
above.
Calculate the difference height, either by logs or machine in the
normal manner. Apply with instrument and signal corrections to the known height
of station to obtain the height of the unoccupied station.
See Figure 12.4.2, for an example computation.

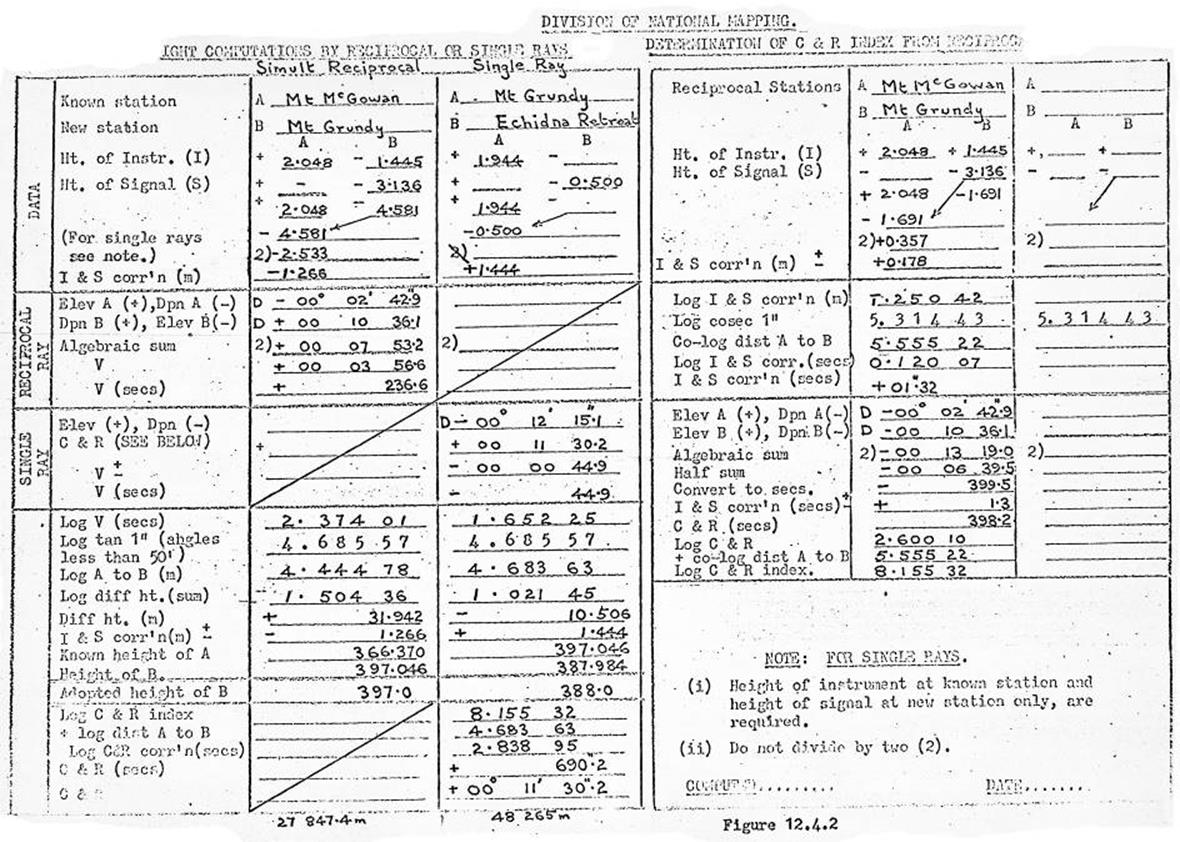
12.5 Astronomical Terms met with in Observations and Computations
Altitude (h)
In the above context, the altitude can be taken as the Vertical
Angle measured between the horizontal plane and the heavenly body.
Arc to Time & vice versa
Computations for Longitude are based on time, and Longitude is
measured in arc. Thus, conversion of arc to time and the reverse is constantly
in use. As the Earth turns once, (i.e. 360°)
on its axis each 24 hours in one hour it turns 15°. Therefore divide Longitude (in arc) by 15 to get Longitude (in
Time), and vice versa.
Azimuth Angle (Z)
Is the horizontal angle at the station zenith, between the
celestial meridian and the great circle passing through the zenith and the
star. This angle may be to the East or West of the meridian, depending
on the Hour Angle (H). If the H is East, or minus, the Azimuth Angle will be on
the eastern side of the meridian, and if the H is West or positive,
the Azimuth Angle will be on the western side of the meridian.
Celestial Equator
The plane of the Equator extended to infinity to cut the Celestial sphere.
Celestial Poles
Points whore prolongation of the Earth's axis cuts the Celestial sphere.
Celestial Sphere
An imaginary sphere, with the Earth as centre, but at infinite
distance from it, on which the “fixed stars” are imagined to be set. At various distances
closer to the Earth, are the planets, sun and moon on their respective orbits.
Culmination
The crossing of the meridian by a heavenly body; i.e. the highest point above the horizon it will reach. Also called “upper
transit".
Co-Latitude (c)
The complement of the Latitude; i.e. 90° - Latitude.
Co-Declination (p)
The complement of the Declination;.i.e. 90° - Declination. Also known as "Polar
Distance”.
Declination (d)
The coordinate of a star which can be considered similar to the
Latitude of a place on the Earth's surface. The star's Declination's are
listed, in arc,
North or South
of the Celestial Equator. See Figure
12.5(a).
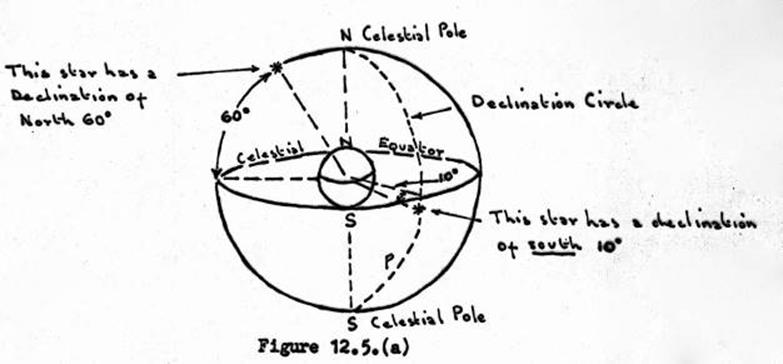
First Point of Aries (g)
An imaginary point on the Celestial Equator from which a star’s
Right Ascension (RA) is measured in Time. RA is always measured from g towards the east, that is
to say, in the opposite direction to that which it travels around tho Celestial
Equator, because g moves with the rest of the fixed stars from
East to West, i.e. clockwise.
Hour Angle (HA)
The easiest way to understand the Hour Angle is by visualizing a
close circumpolar star circling the South Celestial Pole in a clockwise
direction i.e., rising in the east and setting in the west. The Hour Angle,
usually indicated by "t”, is the angle at the Celestial Pole between the
declination circle passing through the star and the Celestial Meridian passing
through the station zenith.
A star East of the station meridian has a negative hour angle equal to the
period of sidereal time that it will take for the star to reach the meridian
(culminate).
A star West of the meridian has a positive hour angle equal to the
period of sidereal time since the star culminated.
Local Sidereal Time (LST)
When the First Point of Aries (g) is on the observer’s meridian the LST is 00 hours.
When a star is on the observer’s meridian, the LST equals that
star's RA.
If it will take a sidereal hour for the star to culminate, the
star's hour angle is -1hr and the LST equals RA -1hr.
An hour after the star has culminated its hour angle is +1hr and the LST equals RA +1hr.
Local Mean Time (LMT)
The instant of mean time that the sun crosses the Local Meridian.
Mean Time
Is the time kept by our clocks and is determined from a so called
"mean sun". This is necessary because :
The inclination of the plane of the Equator to the plane
of the Earth's
orbit around the sun.
The elliptical shape of
the Earth's orbit.
To provide some constant measurement of time by the sun, a
"mean sun” is assumed. This is an imaginary body moving around the
Celestial Equator at a uniform speed, transiting over the meridian each noon at
a regular interval of time equal to the Mean Time of all the days of the year.
Nadir
A point on the Celestial Sphere directly beneath the observer;
i.e. opposite to Zenith.
Sidereal Time (Star Time)
As the movement of the earth around the sun is not obvious to an
observer on the earth's surface, and for the sake of simplicity, he usually
imagines that the earth is fixed, and that the sun and stars revolve around the
earth. Thus, the whole system of "fixed stars" appear to revolve,
with absolute unity, from East to West around the earth. One complete
revolution serves as a convenient unit of time for astronomical purposes. All
the stars complete their circles of revolution in the same period, called the
Sidereal Day. This is 3 minutes
56.56 seconds
shorter than the Mean Time Day.
The datum for sidereal time is 00 hours when the First Point of
Aries crosses the meridian of Greenwich. Thus Greenwich Sidereal Time (GST), at
any instant, is the interval that has elapsed, measured in sidereal hours,
minutes, and seconds, since the last transit of the First Point of Aries across
the meridian.
Tables are available for the conversion of Mean to Sidereal Time
and vice versa; also tables of Sidereal Time at 00 hours UT for each day.
Prime Vertical
Is that particular vertical circle which is at right angles to the
meridian, and which therefore passes through the East-West, points of the
horizon.
Right Ascension (RA)
The coordinate of a heavenly body which can be equated with the
Longitude of a point on Earth, The point from which longitude originates is the
meridian of Greenwich; the point from which RA originates is an imaginary point
known as the First Point of Aries (g).
The RA of a star is listed in time elapsed since the First Point
of Aries last crossed the meridian. See Figure 12.5(b).
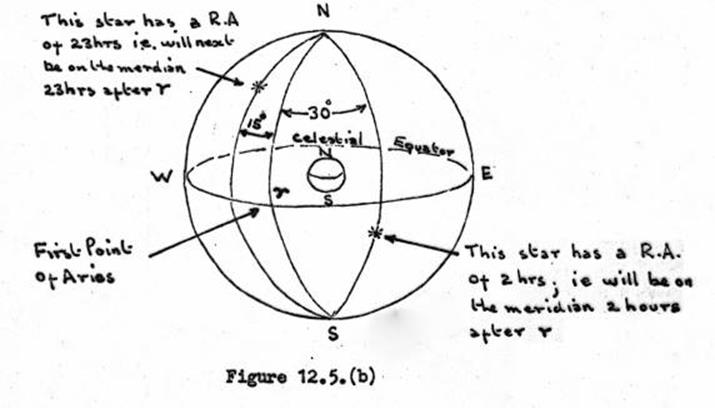
Refraction
The bending of a light ray as it passes through the Earth's
atmosphere.
Various tables, listing corrections, are available; the altitude of the
observed body, barometric pressure and temperature are required.
Sun’s Parallax
The difference between the direction of the sun, as seen from the
place of observation, and as it would be seen from the centre of the earth. A
correction for the Sun’s Parallax, at differing altitudes, is listed in various
tables. This correction does not apply to fixed stars owing to their infinite
distance from the Earth.
Universal Time (UT)
Formerly Greenwich Mean Time. Datum is 00 hours at midnight
Greenwich Mean Time. Standard Times and Time Signals throughout the world and
tables of sidereal time are based on this datum.
Zenith
A point on the Celestial Sphere directly above the observer. The opposite to Nadir.
Zenith Distance (z)
The vertical angle a heavenly body makes with the zenith;
co-altitude, the
complement of
the altitude.
12.6. Time and Time Conversions, Hour Angle
General
The understanding of time is the key to understanding the
movements of the stars, and the location of any selected star; also the observations for Latitude, Longitude and Azimuth. The RA of
heavenly bodies are listed in time; the declination, which is the other
coordinate of the stars is listed in arc; while declination is just as
important in most calculations it is much easier to understand.
In astronomical observations the 24 hour clock code is always
used.
Standard Time
To avoid confusion arising from the use of different local times in various towns and cities, most
countries reckon their Mean Time from the mean time of a particular meridian
(or meridians in large countries such as Australia). The selected meridian is
an exact number of hours, or half-hours
from Greenwich.
In Australia there are 3 standard meridians and thus 3 "Time
Zones" (However, with the introduction of “Daylight Saving Time” in some
States during the summer months there can now be many more “Time Zones” needing
the observer to take special care of just what “time zone” is being used).
The three “standard time zones” are:-
Eastern 150°
or 10 hours East of Greenwich
Central 142.5° or 9.5 hours East of
Greenwich
Western 120° or 8 hours East
of Greenwich
Time Conversions
To convert Standard Time to Local Mean Time (LMT)
Example A. Example
B.
EST 11h 14m 23h
14m
Long. of Station E150° 45¢ E148° 10¢
Long. of Standard Meridian E150° 00¢ E150° 00¢
Station East of Meridian 0° 45¢ Stn. West of
Meridian 01° 50¢
EST 11h 14m 23h
14m 00s
45¢ in time +
0h 03m 01° 50¢ in time - 00h 07m 20s
LMT 11h 17m 23h
06m 40s
Standard time to GMT (UT)
Subtract the longitude (in time) East of the standard meridian from standard time:-
EST 11hr 14min
East Long. of Standard Meridian 10hr 00min
GMT (UT) 01hr 14min
GMT (UT) to Greenwich Sidereal Time (GST)
A sidereal day is shorter than a mean time day by 03m 56.56secs.
A sidereal hour is shorter than a mean time hours by 00m 09.86sec. Thus to
convert an interval of mean time to an interval of Sidereal Time, add, the correction (listed in Chambers Tables and the Star Almanac) to
the mean time interval.
Since Midnight GMT (0hrs UT) 09h 30m have
elapsed.
Convert to Sidereal Time interval 01m 34s
Sidereal interval since 0h U.T. 09h 31m 34s
+ Sidereal Time at 0hrs on 1/3/61 10h 24m 14s
GST
of
observation 20h 05m 48s
GST to LST
To convert the GST to LST all that is now required is to add the Longitude of the station (in time) to the GST of Observation.
GST of observation 20h 05m 48s
+ Longitude of station (in time) 08h 29m 07s (Long. 127° 16' 37.65")
28h 34m 55s
- 24h
00m 00s
LST of observation 4h 34m 55s

Figure
12.6(a) shows at Midnight UT on 1/3/61, the relative positions of the
Greenwich Meridian, the First Point of Aries, and
NM/F/110.
Figure 12.6(b) shows the path of the First Point of Aries across
the meridian of NM/F/110 to a point a further 4hr 34min 55sec towards the Greenwich meridian. As shown GST is
now 20h 05m 48s (i.e. this is the interval which has elapsed since g was last on the meridian of Greenwich.
Thus the 04h
34m 55s which has elapsed since g was on the meridian of
NM/F/110 is the LST of that point.
Determination of the Hour Angle (t)
As mentioned in the definitions, a star East of the Observer’s meridian has a negative Hour Angle. Thus its bearing will lie
between 0° and 180°. Conversely a star West of that meridian has
a positive Hour Angle and its bearing will lie between 180° and 360°.
When a star culminates its HA is zero and the LST is equal to the
star's R.A. If a star has an HA of -1hr and RA of 10hrs the LST will be 9 hrs. Thus if we know the LST and the star's RA the HA can be determined.
Example A. Example B.
LST 9hr 11hr
RA 10hr 10hr
HA (t) - 1hr +1hr
In Example A above, the LST would be 10hr when the star culminates
but as the LST is only 9hr the star must be east of the meridian and must have
a negative HA.
In Example B above, the LST would be 10hr when the star culminates
and as the LST is 11hr the star must have culminated 1hr previously. It is now
west of the meridian and has a positive HA.

Rule to determine the Hour Angle (t)
Subtract the RA from the LST of observation. As the RA is listed
in the 24hr clock mode, if the LST is too small to do this add 24 hours to the
LST. This gives the H.A in the 24 hr clock mode. When computing with
Shortrede's Log Tables the values at the HA, in time, can be read direct from the tables, however, when using the U.S.
Dept of Commerce
Natural Tables, time must be converted to arc. In both these tables values are listed for all quadrants.
12.7.
Computation of Ex-Meridian Sun Observation for Azimuth
It is necessary to solve
the Astronomical Triangle shown in Figures 12.7(a) and (b), the latter being in
plan.
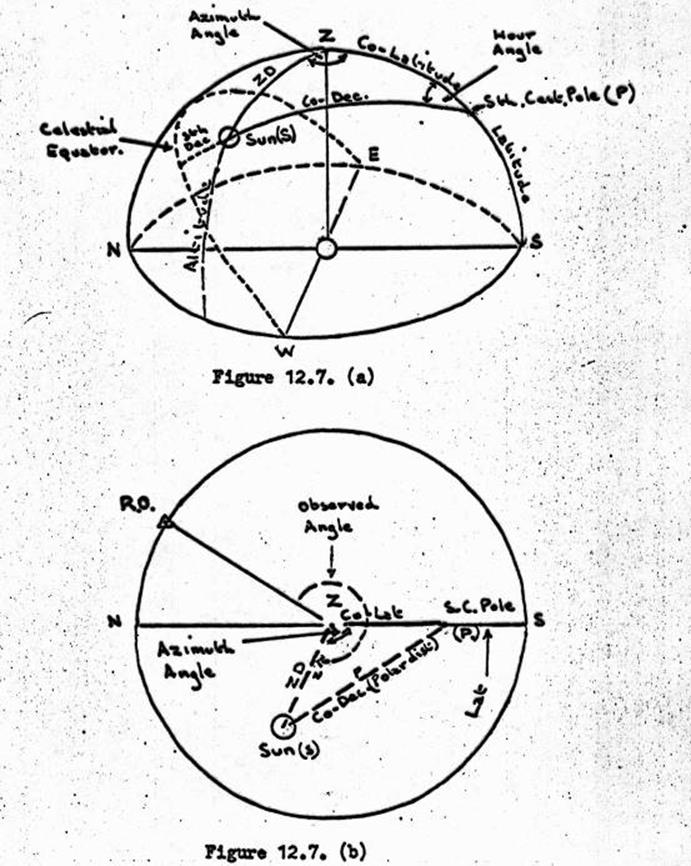
The triangle is made up of the known spherical sides:‑
Zenith Distance or Co-Altitude “z” (From
field observations)
Co-Latitude “c” = 90°
- Latitude. (Scaled from best
available map)
Co-Declination or Polar Distance "p" - either 90° + Nth Dec. or 90°
- Sth Dec. (From
Star Almanac)
After field observations in which vertical and horizontal angles
are read to the sun as a moving target, the problem is to calculate the Azimuth
Angle PZS (known as either "Z" or "A”) to obtain the azimuth
from the oblique spherical triangle PSZ, in which all sides are known in arc.
If Time is required also, the Hour Angle ZPS (known as
"P")
must be
calculated.
Formula:-
For the calculation by Logs, use
Tan (Z/2) = 1 / (sin (s - p )) * Ö((sin (s-z) *sin (s-p) *sin (s -c)) / (sin
s))
where Z is the Azimuth Angle
z is the Zenith Distance
p is the Polar Distance
c is the Co-Latitude
s = (z+p+c)/2
Computing Forms (Log and Natural Tables)
Observed ZD and UT of observations are taken from finalised Field
Book.
The best available Latitude is used in the computation.
The sun's Parallax is obtained from tables on the back of the log
computation form, or from Chambers Tables.
Listed in the Star Almanac, and on the back of the log computation
form are tables for Mean Refraction at a standard pressure of 29.7 in.
(1006Mbs) and a standard temperature of 45°F (7°C). In the Star Almanac are
tables to correct the Mean Refraction Table for pressure and temperature where
considered necessary.
Listed in Chambers Tables are tables for Mean Refraction at a
standard pressure of 29.6 in. (1002Mbs) and a standard temperature of 50°F
(10°C), also with tables to correct for pressure and temp.
Where temperature and pressures are likely to widely depart from
the above, or in special cases where greater accuracy is hoped for, the
required atmospheric readings should be taken immediately before and after the
observation. These are not usually applied in the field check computation.
The Sun's Declination is listed in UT and at 6 hour intervals in
degrees, minutes and decimals of a minute, N or S. The best method to use this table is by converting the 6 hours, and the part of the 6 hours to minutes, and
take a straight proportion of the difference in declination for the six hours
which should be brought to minutes and seconds instead of decimals of a minute.
If available a slide rule can be used to advantage; one setting is made and all
corrections read off at the same time. The multiplication by hand or machine is
quite easy if no slide rule is available.
Example:-
Required, Sun's Dec. at 0822 UT on Friday 22 May, 1970.
Extracts from Dec. Table:
22 Fri. 06hrs N 20° 18.6' (20° 18¢ 30²)
Diff 3.0'
12hrs N 20° 21.6' (20° 21¢ 30²)
Thus the proportion of the 6 hours required is:
2 hr 22 min in 6 hrs of the difference, 3¢ 00"
2hr 22m * 3¢ 00² = 142m * 180² / 360m = 71² or 1¢ 11²
6hr
Thus: Tabular value for 06 hrs N 20° 18¢ 30²
Calc. value for 02hr 22min + 01¢ 11²
Value for 08hr 22min N 20° 19¢ 41²
The rest of the log calculation is a straight forward layout of
the formula. Make use of the diagram to enter positions of the Sun & RO
accurately enough to avoid gross error when inserting the sign of the Azimuth
Angle and checking the true bearing of the RO.
In the calculation using Natural Tables the Cos formula is used:-
Cos Z = ((Sin Dec - (sine Lat * cos ZD)) / (cos Lat * sin ZD))
This formula makes a better layout for a calculation by Naturals
on a proforma. Read the note on the bottom of the form to ensure that correct
sign is given to Cos Z; and that the correct angle is extracted from the
tables.
A way of ensuring that the correct sign for Z always
eventuates for South latitudes automatically, is to reverse the sign of
the declination i.e. North – negative and South – positive. As the ZD and Lat
are POSITIVE the correct sign for Z will be given by the above formula.
Corrections for dislevelment of the Vertical Axis of the
Theodolite
If great accuracy is to be attempted, the plate bubble should be
read at each pointing on the sun. Procedure is the same as laid down for the
observation for Azimuth on Sigma Octantis in section 3.8; notes on ascertaining
the sign of the bubble correction and calculating it are in section 12.8.
Examples of Sun Azimuth computations.
These are shown in Figure 12.7(c) Log computation.
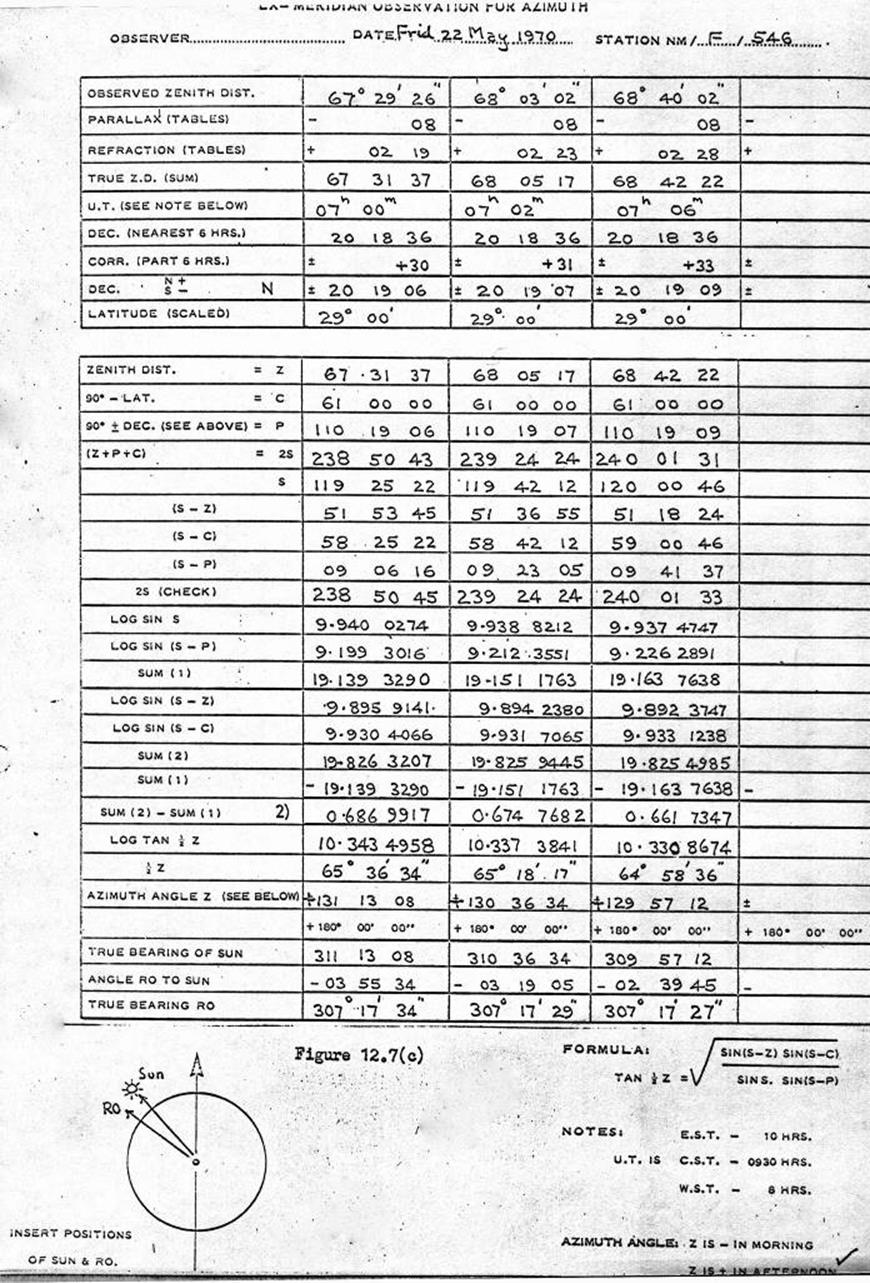
12.8.
Computation of Azimuth from a close Circumpolar Star - Log
or Natural Tables
The usual close circumpolar star used for the determination of
azimuth in Australia is Sigma Octantis. With a declination of approximately 89°
04'S and its fastest movement in azimuth (at upper or lower transit) being only
some 17
seconds of arc
in 1 minute of time makes
pointing easy,
and a time
accuracy of
0.5 seconds is all that is normally required.
Figure 12.8(a) illustrates this slow movement
Movement of Sigma Octantis at various Hour Angles, Latitude 30°.
One quadrant only shown.
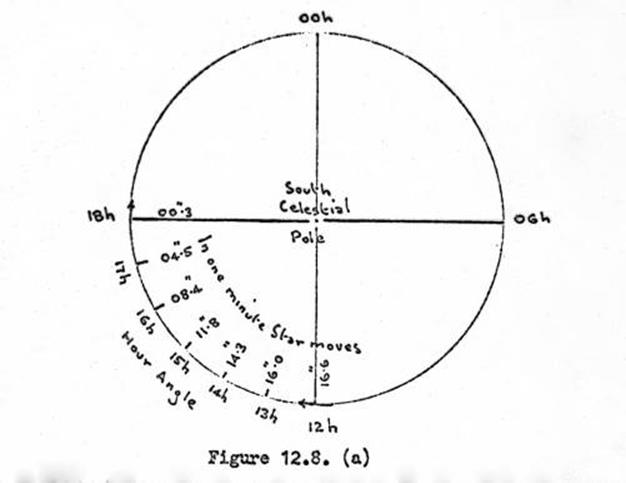
The field book is reduced as described in Section 3.8; the meaned
time of each round reduced to UT, and the mean of each round of horizontal angles is required, also
the vertical angle (nearest minute) and bubble reading.
The Hour Angle of each pair of observations are calculated on the proforma and the corresponding
horizontal and vertical angles entered in their appropriate spaces.
The problem is to calculate the Azimuth Angle which the star made
with the true
meridian at
each of the hour angles. This angle may be to the East or West of the meridian depending on the hour angle. Using the 24 hour
clock code in
all steps from the initial recording of the mean time of the observation to the conversion of the HA to arc, the, decision as
to the
quadrant in
which the star lies at the time of the observation is quite simple.
It must not be forgotten that the requirement for this azimuth computation is a knowledge of the accurate Latitude and Longitude of the
position from which the observations were made.
Formula :
In solving the spherical triangle ZPS (Figure 12.8.(b) this time,
the accurately known values are:-
The side ZP (Co-Lat)
The side PS (Co-Dec. or Polar Distance "p")
The included angle ZPS (Hour Angle "t")
The formula used for the Log calculation is:‑
A" = sec f * p" * sin t +
(p")2 sin t * cos t * tan f
* sin 1"
Where :
A" = Azimuth Angle in seconds or arc
p" = Polar Distance in seconds of arc
t = Hour Angle
f
= Latitude
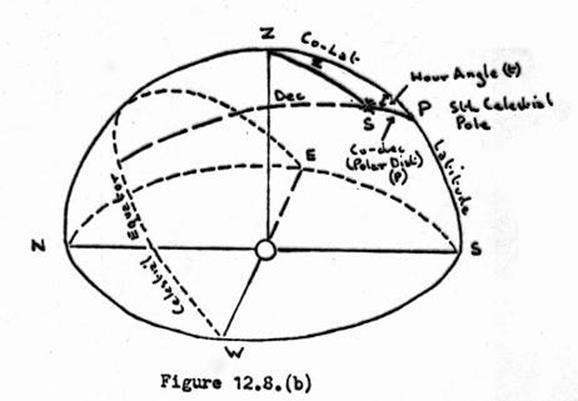
That part of the equation, (p")2 sin t * cos t * tan f * sin 1", gives the small correction for the sign of the sin and does not need
solving, the values being tabulated in Albrechts Tables for ±Log(1/1-a). Where the star is above
elongation the correction is plus, and where the star is below
elongation the correction is minus.
There is a proforma for Natural Tables using the above formula; however the more
straight forward formula and the one in general use within the Division is:‑
A" = ((206264.8 *sine t) / (a-(b * cos t)))
Where :
a = sin f and
b = (sin dec * cos f / cos dec)
A proforma is available for this formula and all these proformae are straight forward as long
as the signs of the angles in their various quadrants are watched carefully.
Shortrede’s Log Tables show this clearly as do the 8 figure U.S. Dept of
Commerce Sine & Cosine Natural Tables. The Secant can be obtained by 1/cos
and the Tan Dec (nearest Minute) from Chambers Tables.
Determination of Azimuth from the Azimuth Angle
The proforma probably makes this explanation redundant, however
the understanding of the problem is important in case computations have to be
done when no proforma is available.
As the azimuth of the meridian from the station to the South Pole is 180°, and the computation has been to
find the angle that the star made with this meridian (azimuth angle), the star’s azimuth is obtained by :
Subtracting the azimuth angle from 180° if the star is East of
the meridian, or adding the azimuth angle to 180° if the star is West of the meridian.
Once the azimuth to the star has been computed, the azimuth to the
R.O. can be determined by applying the
horizontal angle. As the clockwise angle from the R.O. to the star is always observed, the
azimuth to
the R.O. is arrived at by subtracting the horizontal angle from the azimuth of the star.
If the
azimuth of the star is less than the horizontal angle, add 360° to the azimuth of the
star, before subtraction.
180° 00'
00"
Azimuth angle - 40’
25.2
Azimuth or Sigma Octantis 179 19 34.8
Add 360° 360 00 00
539 19' 34.8
Subtract angle RO to Star 262 05 51.4
Azimuth to RO 272
13 42.4
Note :
Sketch not to scale,
Azimuth angle has been exaggerated.
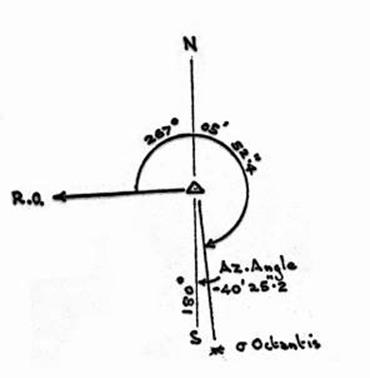
Figure
12.8. (c) Determination of azimuth from azimuth angle.
Time curvature correction
Where undue delay between FL & FR pointings on the star has been caused by cloud,
etc., a correction is necessary. Figure 12.8.(d) gives a table for this correction,
the formula is from Bomford's "Geodesy". In general practise,
however, it has been found better to discard such pointings in the field and observe additional
rounds to take their place.
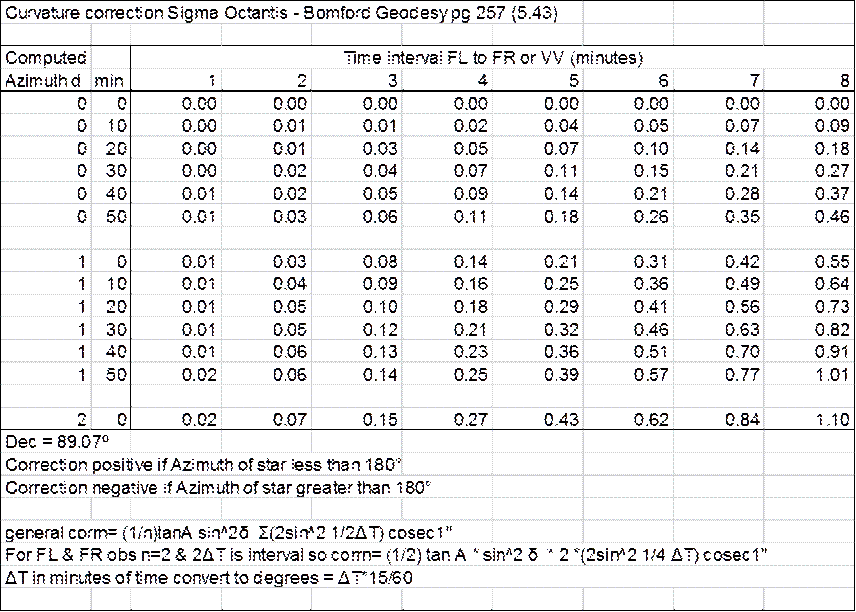
Figure
12.8.(d)
Plate bubble corrections to astronomical observations for azimuth
The first principle to get clearly in mind is that the azimuth of the star, as calculated is correct, and dislevelment of the
theodolite as shown by the plate bubble bears no part in this result as it was calculated from accurate Time, Latitude, Longitude and
the astronomical co-ordinates, of the star.
The second principle is that the bubble correction for dislevelment is applied to the
horizontal angle, R.O. to star.
The correction to the horizontal angle is :
If readings are high (+), to the left, the instrument is tilted to
the right, therefore the instrument
read a horizontal angle which was too small, thus the correction must be added to the observed angle. See
Figure 12.8.(e).
If readings are high (+) to the right, the instrument is tilted to the left, therefore it read a horizontal angle which
was too large and the correction must be
subtracted from the observed angle. See Fig. 12.8.(f).
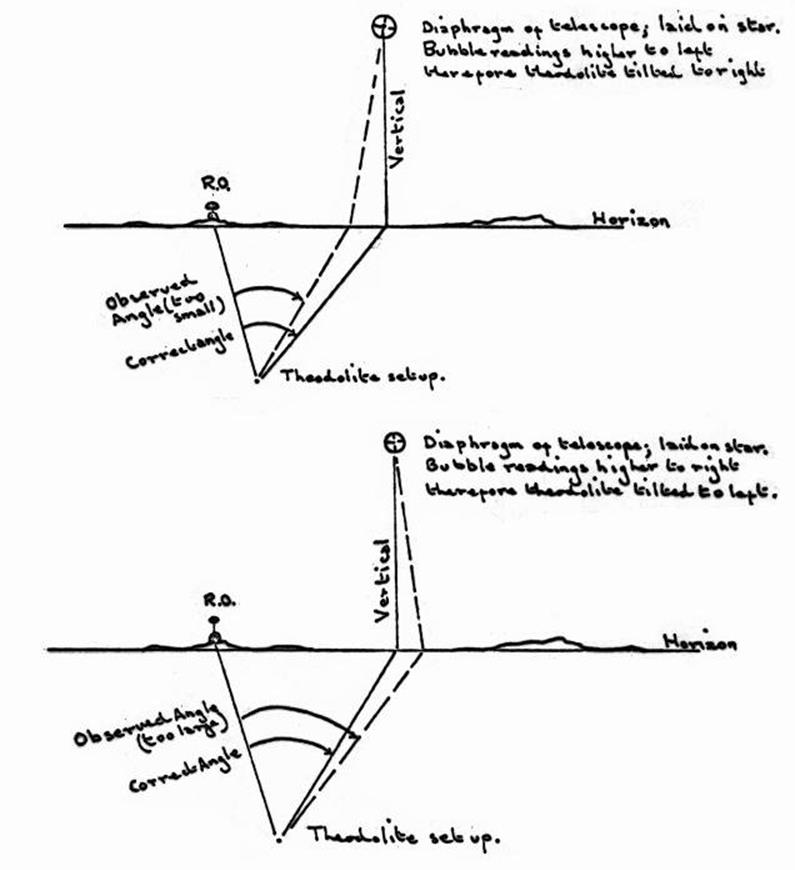
Figures 12.8.(e)
and 12.8.(f).
The bubble is read from the centre outwards; the values being estimated to 0.1 of a division. They
are recorded Left & Right, as seen from the stance of the observer. In the case of a close circumpolar star, in the
Southern Hemisphere,
the field books show East for Left and West for Right. The layout of the plate bubble of the Wild Theodolites and suggested method of reading them, is :
Plate Bubble Wild T2, Plate
Bubble Wild T3.
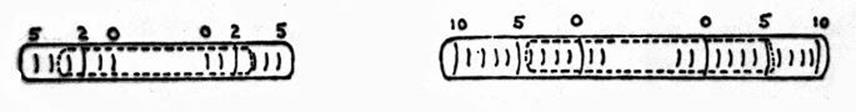
+L 3.7 -R 2.9 +
L 4.2 - R 5.3
1 Div. = approx 20" 1
Div. = approx 6.5"
To calculate the bubble correction in divisions and decimals
(Sum L - Sum R)/n = correction, where n is the number of ends read.
To calculate the bubble correction in seconds of arc
Tan Alt x bubble corr'n (in Divs & decimals) x value 1 Div of
bubble =
Correction
Example
L. R.
5.0 5.6 Altitude 29° 57’
5.0 5.6 1 Div = 6.5”
4.7 5.3
4.6 5.4
+19.3 -21.9
+19.3
-2.6 -2.6/8 (ends) = -0.32
Bubble Corr'n = Tan (29° 57’) * (-0.32) * (6.5”) = -01.20"
Observed Horizontal angle 271°
49’ 36.2”
Bubble correction -01.2"
Corrected Horizontal angle 271° 49’ 35.0”
True bearing star 178° 56’ 47.6” (add 360°)
- Corrected Horizontal angle 271° 49’ 35.0”
True bearing R.O. 267° 07’ 12.6”
Special Note :
When using the proforma for observations on close circumpolar stars, to avoid the extra
step of correcting the horizontal angle before subtracting it from the true
bearing of the star, the signs printed on the form for the calculation of the
bubble correction
have been
reversed, so that
the correct true bearing is obtained by just applying the correction straight to the uncorrected bearing of the R.O. Also,
as previously mentioned, Left is listed as East, and Right as West.
The above example as it would appear on the Proforma :
Example
E W
5.0 5.6 Altitude 29° 57’
5.0 5.6 1 Div = 6.5”
4.7 5.3
4.6 5.4
-19.3 +21.9
-19.3
+2.6 +2.6/8 (ends) = +0.32
Bubble Corr'n = Tan (29° 57’) * (+0.32) * (6.5”) = +01.20"
True bearing star 178° 56’ 47.6” (add 360°)
Observed Horizontal angle 271°
49’ 36.2”
Uncorrected bearing R.O. 267° 07’ 11.4”
Bubble
correction +01.2"
True bearing R.O. 267° 07’ 12.6”
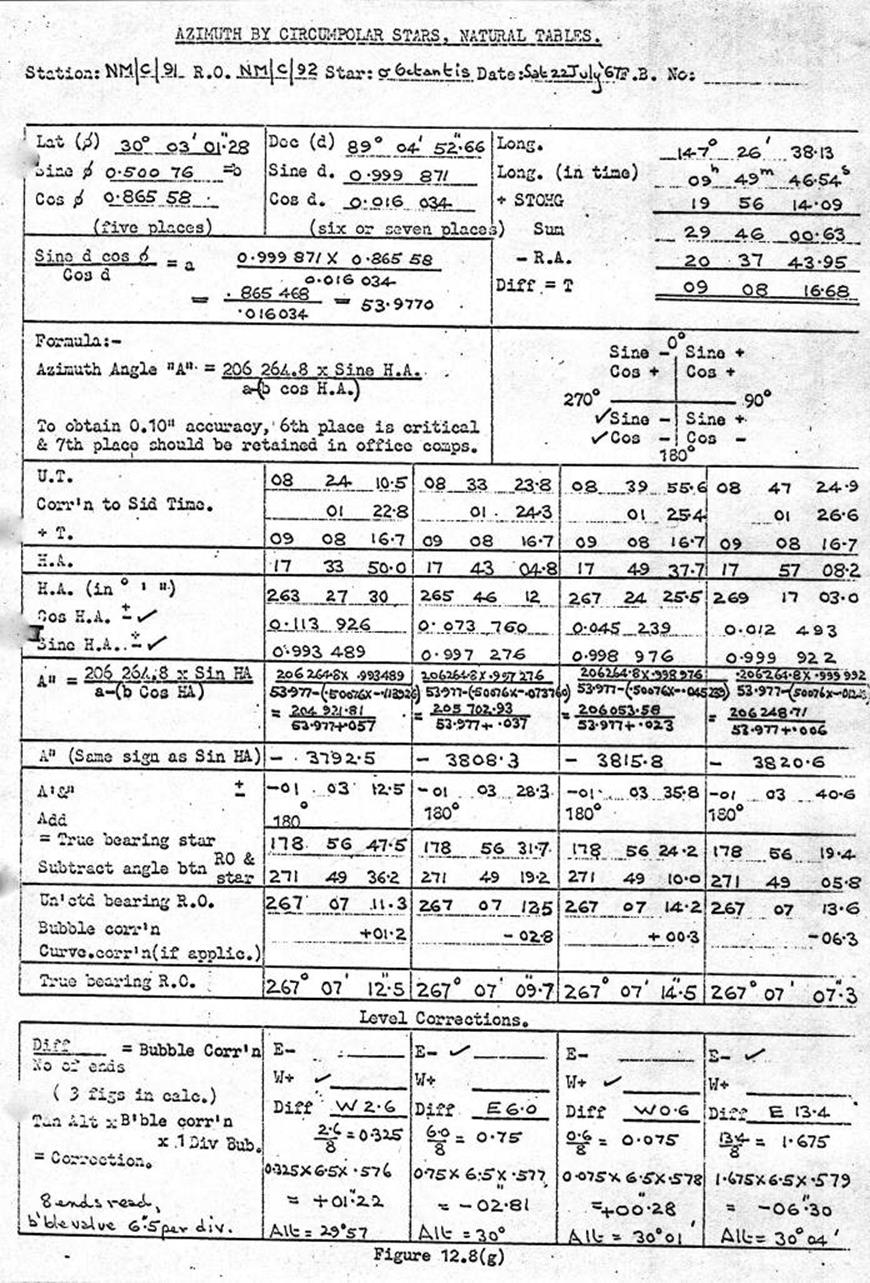
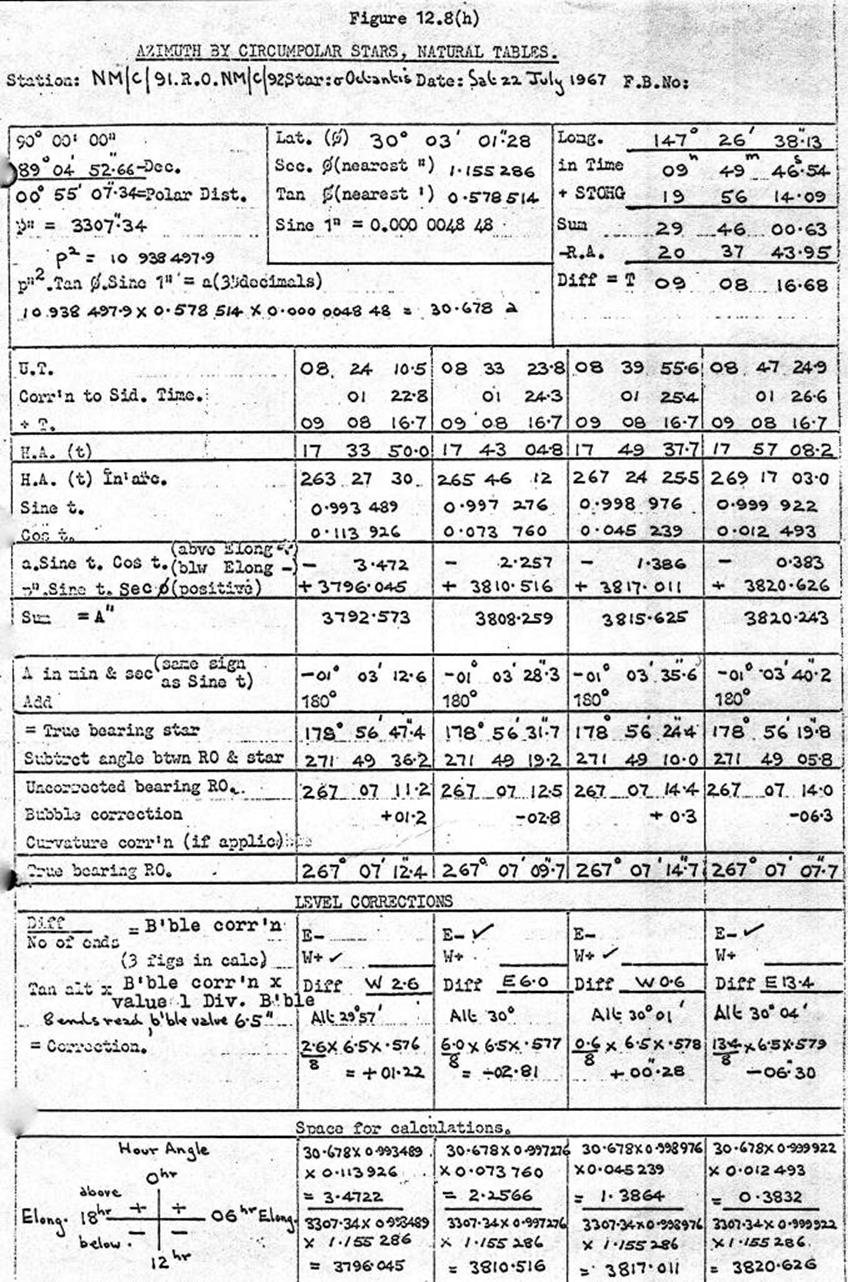
Interpolation of the R.A. & Declination of Sigma Octantis
From the Star Almanac
A table is given showing the apparent position of Sigma Octantis
for every tenth Upper Transit at Greenwich. Positions are given to the nearest
second of Time in R.A., and the nearest second of Arc in Declination.
For the accuracy required in the field computation, and taking
into account the accuracy of the table, a direct interpolation to the day of
observation is sufficient.
From the FK4
A table is given showing the apparent position of Sigma Octantis
for every Upper Transit at Greenwich. Positions are given to two decimals of a
second of time in R.A., and to two decimals of a second of arc, in Declination.
For the field computation, the values tabulated for the time of
Upper Transit at Greenwich, are sufficiently accurate without interpolation. In
the extreme case the error in the field computation will only be about
0.5", in the computed azimuth.
If very accurate results are required, it is necessary to ascertain
the U.T. of Upper Transit on the day of observation, and interpolate between
this and the U.T. of the observation. This is not quite straightforward;
depending on the Sidereal Time at 0hrs U.T. and the R.A. of Sigma Octantis, the
interpolation may be forward towards the next day, or backwards towards the
previous day’s value.
The following examples illustrate the problem :
Example 1 : Where Siderial Time at 0hrs U.T. is less than R.A.
Date of Observation, 17 Jan 1971.
U.T. of Observation (approx mean time of whole observation) 14h
24m
U.T. of Observation (in days and decimals of a day) 17.60d
R.A. of Sigma Octantis same date (nearest minute here) 20h
39m
Where R.A. is less than Siderial Time add 24 hrs.
- Siderial Time at 0hrs U.T. same date
7h 43m
U.T. of Upper Transit Sigma Octantis 17 Jan 12h
56m
U.T. of Upper Transit (in days & decimals) 17.54d
Thus the tabulated value in the FK4 for the Upper Transit of Sigma Octantis is for the 17.54 day of Jan,
1971. The observation was done at 17.60, therefore the amount of interpolation
is for 0.06 of a day from the tabulated time of Upper Transit on 17th
towards that of the 18th.
FK4 value on 17 Jan. RA 20h 39m 20.65s Dec. -89°
04’ 13.08”
FK4 value on 18 Jan 20 39 20.49 -89° 04’
12.72”
0.16
0.36
0.06 x 0.16 = 0.010 0.06 x
0.36 = 0.022
FK4 values 17th RA 20 39 20.65 Dec. -89 04 13.08
Corrections -.01
- .02
Values at time of Obs 20 39 20.64 -89 04 13.06
Figures 12.8 (i) and (j) illustrate the above problem.
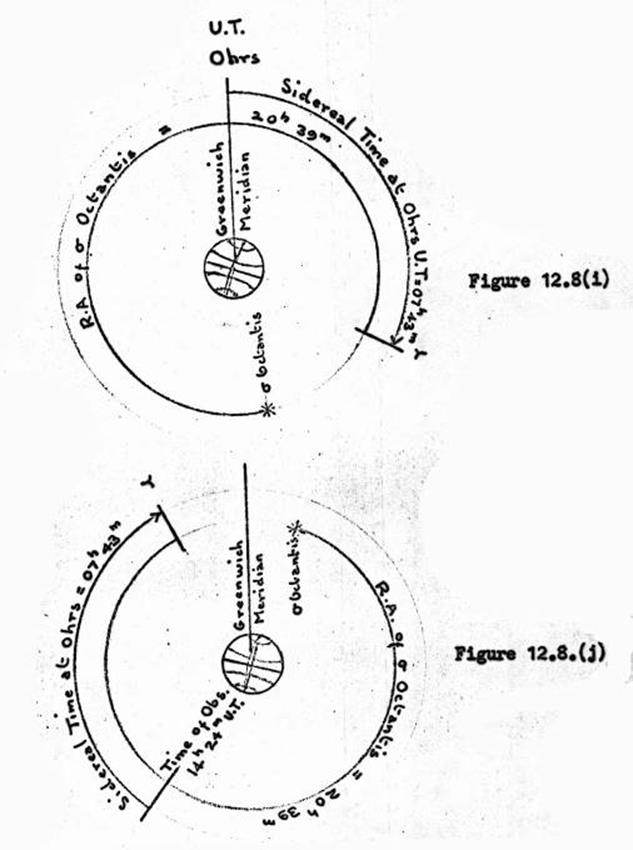
At 0hrs U.T. 17 January 1971. Figure
12.8.(i) shows the positions of g
and Sigma
Octantis. It
can be seen that Sigma Octantis will reach Upper Transit at about 13hrs on the 17th (i.e. in days &
decimals, 17.54).
At 14h 24m U.T. same day (Time of Observation). In Figure 12.8.(j) it can be seen that Sigma Octantis has recently crossed the Greenwich Meridian,(i.e. Upper Transit
when its
values are
tabulated). Thus
the interpolation must be forward from the tabulated value of that day by about 1.5hrs, or 0.06 of a
day.
Example 2 : Where Siderial Time at 0hrs U.T. is greater than R.A.
Date of Observation, 18 Sept 1971.
U.T. of Observation
(approx mean time of whole observation) 09h 08m
U.T. of Observation (in
days and decimals of a day) 18.38d
R.A. of Sigma Octantis
same date (nearest minute here) 20h 42m
Where R.A. is less than
Siderial Time add 24 hrs.
- Siderial Time at 0hrs
U.T. same date 23h 45m
U.T. of Upper Transit
Sigma Octantis 18 Sept 20h 57m
U.T. of Upper Transit (in
days & decimals) 18.87d
Thus the tabulated value
in the FK4 is for the 18.87 day of Sept, 1971. The observation was done at
18.38, therefore the amount of interpolation is for 0.49 of a day from the
tabulated time of Upper Transit on 18th backwards to that of the 17th.
FK4 value on 18 Sept RA 20h
42m 21.19s Dec. -89° 04’ 11.21”
FK4 value on 17 Sept 20
42 22.13 -89° 04’ 10.95”
0.94 0.26
0.49
x 0.94 = 0.461 0.49 x 0.26 = 0.127
FK4 values 18th RA 20
42 21.19 Dec. -89 04 11.21
Corrections
+.46 - .13
Values at time of Obs
20 42 21.65 -89 04 11.08
Figures 12.8 (k) and (l)
illustrate the above problem.
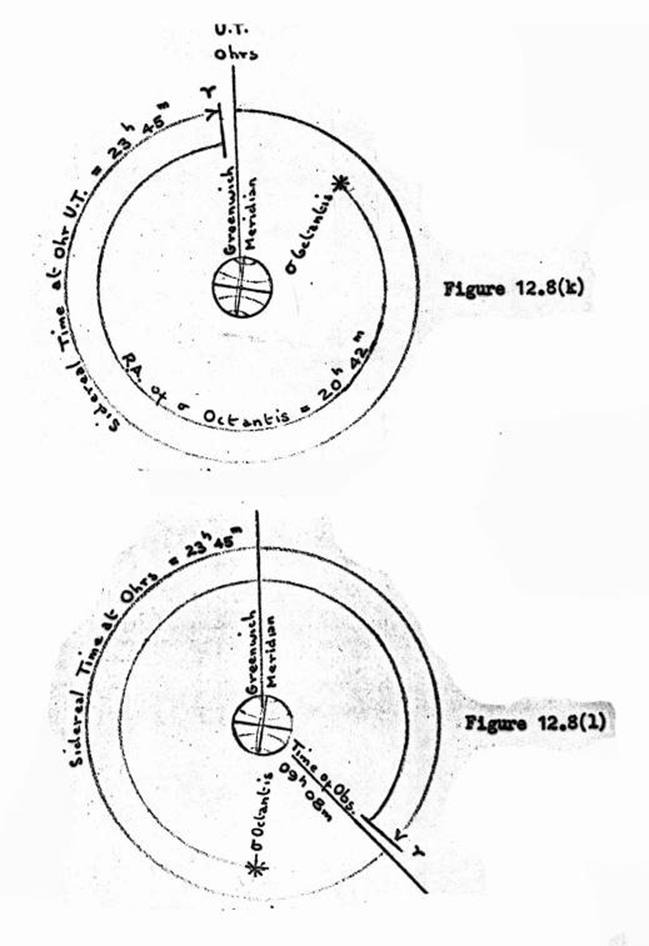
At 0hrs U.T. 18 Sept. 1971. Figure 12.8.(k) shows the
positions of g and Sigma Octantis. It can
be seen that Sigma Octantis will reach Upper Transit at about 21hrs U.T. on the
18th (i.e., actually in days & decimals, 18.87).
At 09h 08m same day (Time of
Observation).
In Figure 12.8.(l) it can be seen that Sigma Octantis has still a long way to go to reach Upper
Transit. Thus the interpolation must be backwards from the tabulated values of the date of observation, towards the previous days' values. The
amount is
about 12 hours, i.e. about 0.50 days.
Example 3 : On the date of the Double Upper Transit
Date of Observation, 2 Aug 1971.
U.T. of Observation
(approx mean time of whole observation) 09h 36m
U.T. of Observation (in days
and decimals of a day) 02.40d
R.A. of Sigma Octantis
same date (1st Upper Transit) 20h 42m 37.33s
- Siderial Time at 0hrs
U.T. same date 20h 39m 44.86s
U.T. of Upper Transit
Sigma Octantis 2 Aug 02m 52.47s
U.T. of 1st
Upper Transit (in days & decimals) 02.002d
R.A. of Sigma Octantis
same date (2nd Upper Transit) 20h 42m 37.60s (+24hrs)
- Siderial Time at 0hrs
U.T. next day 20h 43m 41.42s
U.T. of 2nd
Upper Transit Sigma Octantis 2 Aug 23h 58m 56.18s
U.T. of 2nd
Upper Transit (in days & decimals) 02.999d
Thus it can be seen that the interpolation can be taken forward from the
First Upper Transit, or backwards from the second Upper Transit. In this
example, the interpolation is taken forward from the First Upper Transit.
Time and date of observation 02.400
U.T. of 1st Upper Transit 02.002
00.398
Thus the interpolation is 0.398 forward from the 1st Upper transit towards the 2nd Upper Transit.
FK4 value 24 Aug (1st
Upper Transit) RA 20h 42m 37.33s Dec. -89° 03’ 58.02”
FK4 value 24 Aug (2nd
Upper transit) RA 20 42 37.60 -89° 03’ 58.27”
0.27 0.25
0.398
x 0.27 = 0.107 0.398 x 0.25 = 0.099
FK4 values 1st
Upper Transit 20h 42m 37.33s Dec. -89° 03’ 58.02”
Corrections
+.11 +.10
Values at time of Obs 20h
42m 37.44s -89° 03’ 58.12”
Formula for all above cases :
n (#) = Y - Z
where :
n is the decimal of a day for which interpolation is required.
Y is the decimal of a day for the time of observation.
Z is
the RA of Sigma Octantis for the day of observation minus Siderial Time at 0hrs U.T. same day
(converted to decimals of a day).
(#) If n is positive, interpolate forward from the day of observation to the next day.
If n is negative, interpolate backwards from the entries for the day of observation towards the previous day.
Time curvature correction.
This is only rarely needed in computing Sigma Octantis azimuth
observations. The correction is necessary if there is a long time deiay between
the FL and
FR pointings on the star. Once the observer is experienced, this
time delay would
not be worth taking into account, and would only occur under cloudy conditions. However, under such conditions, it
is advisable that once the time delay reaches about 7 minutes without the star re-appearing,
that arc be abandoned and a fresh start made from the RO when the sky has cleared.
Figure 12.8.(d) gives a time correction table. It is compiled from the formula in Bomford's
"Geodesy", Page 257.
12.9 Barometric
Heighting with Mechanism Barometers – Field Computation
12.9.1 Figure 12.9(a) shows in general terms what is involved
in calculating
difference heights by comparative Barometric readings and is enlarged upon in the
following notes.
Step 1. Base & Remote
Baro's read simultaneously at Base before the Remote is taken to the Remote Station.
Step 2. Base &Remote Baro’s
read each hour, on the hour while the instruments are apart.
Step 3. Base & Remote
Baro' s read simultaneously at Base immediately the Remote returns from the
Remote Station
______^___________
-------------------------
Base (at BM) While
Baro's are being read during the day it is assumed that the pressure at this
point is the same as at the Base. ^
|
Difference between Base readings
and Remote readings |
(after allowing for
instrument comparison) gives |
difference in height in
millibars. |
v
_______________________^______
Remote
Figure
12.9(a).
Field Book
The page in the field book
has been designed so that no transcription to data sheets for programming is
required, a photocopy of the field book page being sufficient. Thus it is
important that all entries are clearly and neatly written in the correct space.
The Base Barometer
readings are transcribed from the Base Barometer book on return from the Remote station. This
transcription should be checked by a second person, as these transcribed
readings are those which will be used in the computations.
Normally, while the
instruments are apart, all readings will be taken on the even hour, however if
this has not been the case, the Base readings must be taken from the graph at
the same instant of time as the Remote readings. It is normal practise to draw
a graph of both Base & Remote station readings. If the curves are not
generally parallel, unsuitable weather conditions, or errors in reading the
barometers are indicated and unreliable heights can be expected. Generally two
instruments are used at each position.
Details of the
Computation.
The computation is a
simple one and the accuracy of the results rely on the comparatively stable
weather conditions generally covering inland Australia. Thus all that is
involved is :
(i)
The
simultaneous comparison of Base and Remote Barometers immediately before
leaving for, and after returning from, the Remote Station; this enables the
Base instruments pressure readings, while the instruments were apart to be
adjusted to the same scale value as the Remote instruments. Temperatures taken
at each station, at the time of all readings are also necessary.
(ii)
The
difference between the "adjusted pressure" at the Base, (i.e., the
mean of all the readings at the Base while the instruments were apart, plus or
minus the "adjustment") and the mean of all the readings at the
Remote Station, (i.e., Mean Remote Pressure) gives the difference height in
pressure, in millibars. This is converted to feet/metres to give the difference
height between the stations.
(iii)
As the
value of the millibar in feet varies with the temperature of the column of air
and the height above sea level, the pressure at the mid height between
stations, and the mean of the temperature road at the stations, is required in
the calculation. Thus the difference height in feet is calculated as a simple
proportion from the difference height in pressure, allowing for the mean
temperature.
Steps to be followed in the computation :
1.
Comparison
of simultaneous
Base and Remote readings (taken before and after visiting the Remote Station).
The difference is found
between these means of Base and Remote instruments. This difference is the
amount needed to "adjust" to the same scale, the Remote and Base
instruments. Note that the Base is "adjusted" to agree with the
Remote. This completes the "Comparison of Instruments", section of
the computation.
2.
Calculation
of Difference Height
(in pressure)
The "adjustment"
is now applied to
the mean of
all the Base readings taken
while, the instruments were apart, i.e., while the Remote instruments were at the Remote
Station. The difference between the adjusted pressure at the Base and the mean
pressure of all the readings at the Remote Station gives the Difference Height in pressure.
3.
Temperature
Correction
The Mean Temperature in °C + 273 = Temperature Absolute.
Temperature Absolute x 95.977 = K, which gives the value of the millibar at that temperature at sea level.
Tables to °C are available for these K factors.
4.
Calculation
of the Difference
Height in feet from the Difference Height in pressure
Difference Height in pressure
Mid. Height in pressure x
K gives Diff. Height in feet
(taking into account the
mean temperature)
Finalising the Calculation
The Base is normally
established at a BM, or close enough to enable a Level connection to be made to the BM. The difference
height between the Base and the Remote Station obtained by the Barometric Heighting, is applied to
the reduced level of the Base Station to give the height of the Remote Station,
in feet; convert to metres if necessary.
Examples of Field Notes
and the Calculation of the Remote Station
height
Figure 12.9(b) shows a
field book page showing entries taken at the Remote Station and the simultaneous entries
transcribed from the Base Barometer Book.
Figure 12.9(c) shows a
graph of the Baro readings at the Base and Remote Stations. All instruments are
graphed separately.
Figure 12.9(d) illustrates
a height calculation on the most simple of proforma for field use.
Figure 12.9(e) illustrates
the same calculation on a more complicated form which takes into account a time
differential when calculating the adjustment to be applied to the Base readings. However,
practise has shown this correction is not warranted in field calculations, as
any variation to the amount of the adjustment is negligible. i.e., Nil to 0.05 Millibars.
Figure 12.9(f) shows a Table of Corrections for
K, where:
K= 95.977 *(°C + 273) from above for
answer in feet or
K= 29.25 *
C +273) for answer in metres.
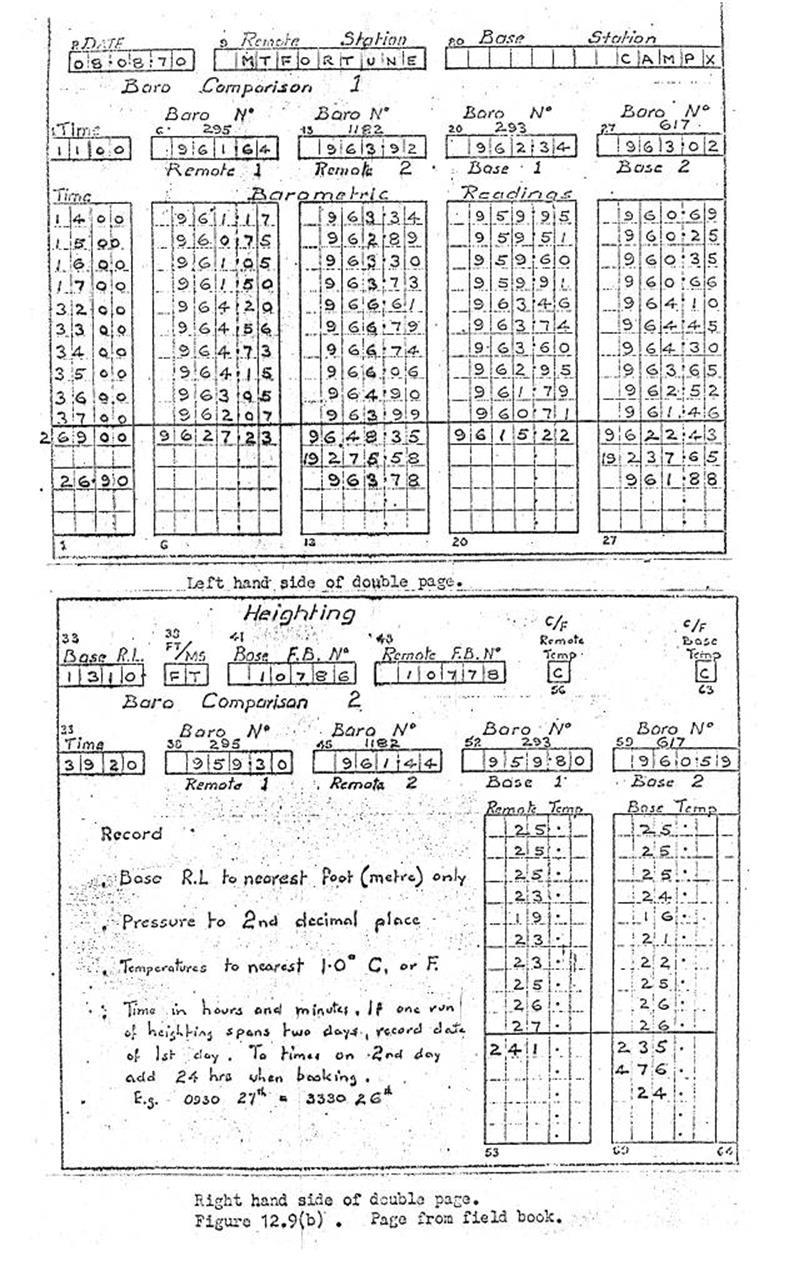
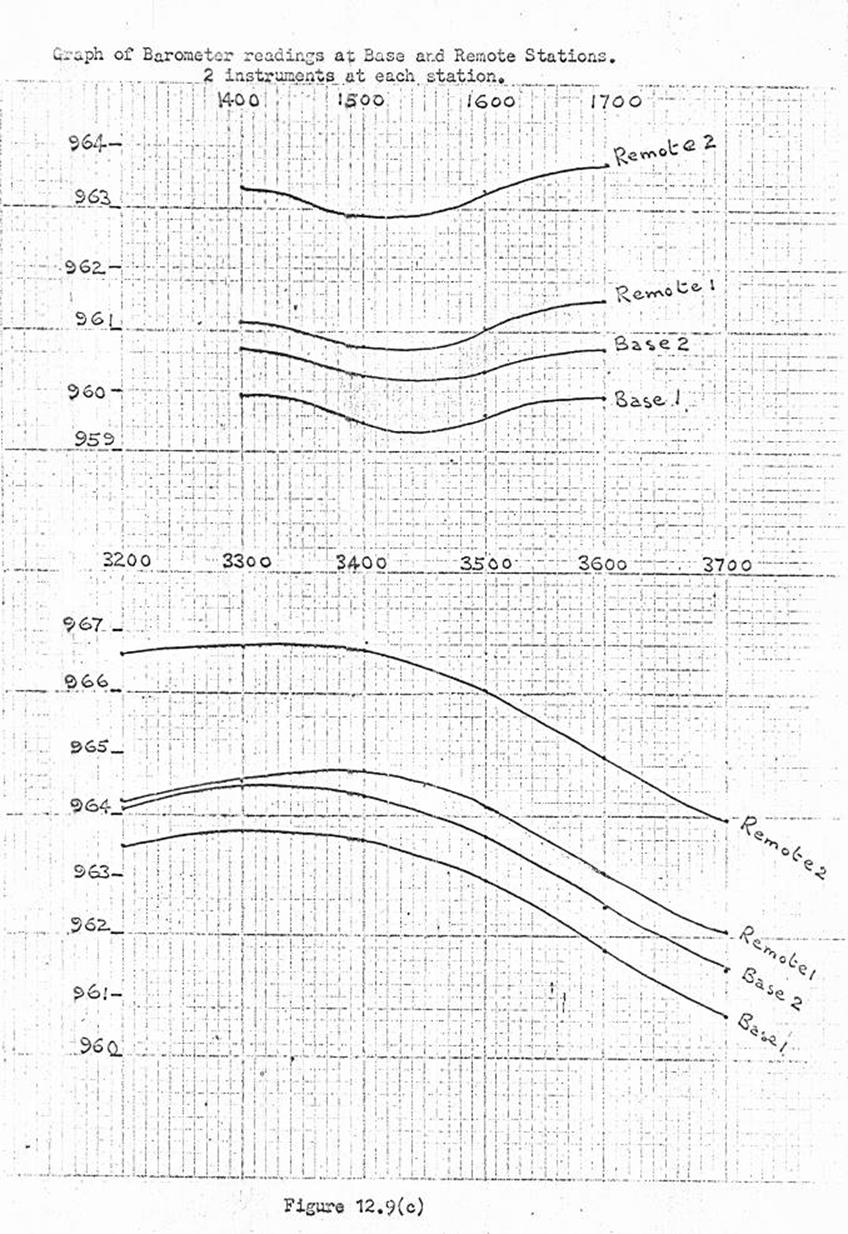
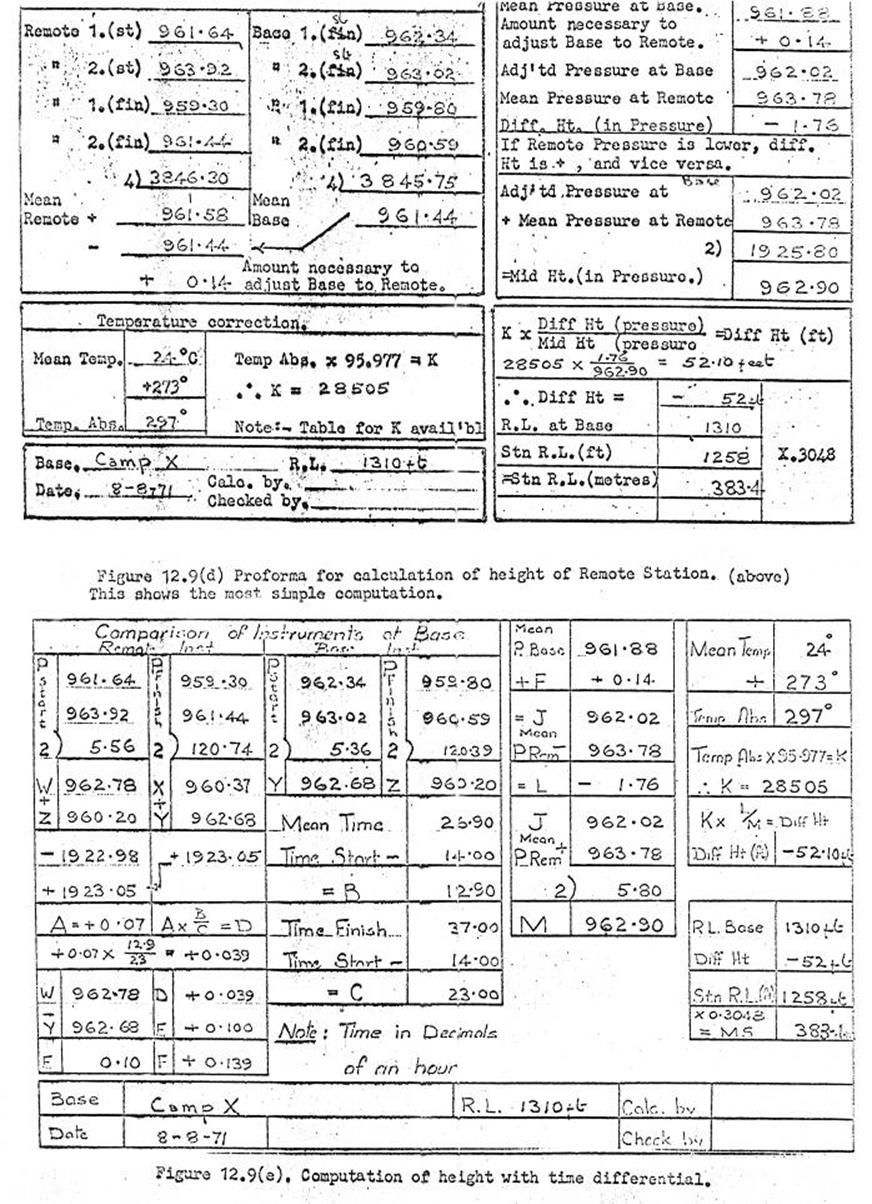
|
"K"
FACTOR FOR TEMPERATURE CORRECTION
|
|
K = 95.977 *(°C + 273) for
feet or 29.25 *(°C + 273) for metres
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Deg C
|
K (ft)
|
K (m)
|
Deg C
|
K (ft)
|
K (m)
|
Deg C
|
K (ft)
|
K (m)
|
Deg C
|
K (ft)
|
K (m)
|
|
0
|
26202
|
7985
|
12
|
27353
|
8336
|
24
|
28505
|
8687
|
36
|
29657
|
9038
|
|
0.5
|
26250
|
8000
|
12.5
|
27401
|
8351
|
24.5
|
28553
|
8702
|
36.5
|
29705
|
9053
|
|
1
|
26298
|
8015
|
13
|
27449
|
8366
|
25
|
28601
|
8717
|
37
|
29753
|
9068
|
|
1.5
|
26346
|
8029
|
13.5
|
27497
|
8380
|
25.5
|
28649
|
8731
|
37.5
|
29801
|
9082
|
|
2
|
26394
|
8044
|
14
|
27545
|
8395
|
26
|
28697
|
8746
|
38
|
29849
|
9097
|
|
2.5
|
26442
|
8058
|
14.5
|
27593
|
8409
|
26.5
|
28745
|
8760
|
38.5
|
29897
|
9111
|
|
3
|
26490
|
8073
|
15
|
27641
|
8424
|
27
|
28793
|
8775
|
39
|
29945
|
9126
|
|
3.5
|
26538
|
8088
|
15.5
|
27689
|
8439
|
27.5
|
28841
|
8790
|
39.5
|
29993
|
9141
|
|
4
|
26586
|
8102
|
16
|
27737
|
8453
|
28
|
28889
|
8804
|
40
|
30041
|
9155
|
|
4.5
|
26634
|
8117
|
16.5
|
27785
|
8468
|
28.5
|
28937
|
8819
|
40.5
|
30089
|
9170
|
|
5
|
26682
|
8132
|
17
|
27833
|
8483
|
29
|
28985
|
8834
|
41
|
30137
|
9185
|
|
5.5
|
26730
|
8146
|
17.5
|
27881
|
8497
|
29.5
|
29033
|
8848
|
41.5
|
30185
|
9199
|
|
6
|
26778
|
8161
|
18
|
27929
|
8512
|
30
|
29081
|
8863
|
42
|
30233
|
9214
|
|
6.5
|
26826
|
8175
|
18.5
|
27977
|
8526
|
30.5
|
29129
|
8877
|
42.5
|
30281
|
9228
|
|
7
|
26874
|
8190
|
19
|
28025
|
8541
|
31
|
29177
|
8892
|
43
|
30329
|
9243
|
|
7.5
|
26922
|
8205
|
19.5
|
28073
|
8556
|
31.5
|
29225
|
8907
|
43.5
|
30377
|
9258
|
|
8
|
26970
|
8219
|
20
|
28121
|
8570
|
32
|
29273
|
8921
|
44
|
30425
|
9272
|
|
8.5
|
27018
|
8234
|
20.5
|
28169
|
8585
|
32.5
|
29321
|
8936
|
44.5
|
30473
|
9287
|
|
9
|
27066
|
8249
|
21
|
28217
|
8600
|
33
|
29369
|
8951
|
45
|
30521
|
9302
|
|
9.5
|
27114
|
8263
|
21.5
|
28265
|
8614
|
33.5
|
29417
|
8965
|
45.5
|
30569
|
9316
|
|
10
|
27161
|
8278
|
22
|
28313
|
8629
|
34
|
29465
|
8980
|
46
|
30617
|
9331
|
|
10.5
|
27209
|
8292
|
22.5
|
28361
|
8643
|
34.5
|
29513
|
8994
|
46.5
|
30665
|
9345
|
|
11
|
27257
|
8307
|
23
|
28409
|
8658
|
35
|
29561
|
9009
|
47
|
30713
|
9360
|
|
11.5
|
27305
|
8322
|
23.5
|
28457
|
8673
|
35.5
|
29609
|
9024
|
47.5
|
30761
|
9375
|
Figure 12.9(f).
12.9.2 Alternative
formula for computation by logs
For general interest,
rather than for field use, the following notes have been compiled from a paper
by Lt-Col. C.A.Biddle, R.E., Senior Lecturer in Surveying, University College,
London.
“If simultaneous readings
of pressure have been obtained at two points, a & b, the text book relation
connecting their height difference (hb - ha) with pressure readings pa and pb,
is usually given in the form:-
hb - ha = { c *(Log
(Pa / Pb)) * (Tm / Ts) } * (1+x)(1+y) where:
c is some constant
Tm is the absolute mean
temperature of the air column between a & b
Ts is the standard
temperature
x is a small
correction for the humidity of the air column
y is a very small
correction for the change in gravity with Latitude.
This formula can be
considerably simplified.
Since Ts is a constant, we
can write (c/Ts) = K, also, an increase
in humidity has a similar effect to an increase in Tm. Instead of using the
separate multiplying factor (1+x) for a humidity correction, we may add to Tm
the small temperature correction Th which would have the same effect.
Similarly, we may replace the gravity change factor (1+y) by adjusting the
temperature again by the correction for Ti of equivalent effect. The adjusted
temperature Tm + Th + Ti may then be known as the virtual temperature, Tv; it
is the temperature of the air column of zero humidity at standard Latitude
which would exert the same pressure as the actual column of temperature Tm. For
most purposes the humidity and Latitude corrections may be neglected
altogether; the former will be insignificant at low temperatures, the latter in
Latitudes between 30° and 60°.
The formula thus reduces
to:-
(hb – ha) =
KTv (log(pa/pb))
Since log tables are
required for one term above, it will be most convenient to complete the
computation by logs.
log (hb – ha) =
log (KTv) + log(log pa – log pb)
A table of log KTv, to
give height difference in feet is at the end of this extract to five figures.
This is sufficient as it will not be worthwhile giving final height differences
more accurately than to the nearest foot”. Note KTv is also given to aid
computation by machine.
Example
of height computation using the above Log formula
Calculation
for feet metres
Pressure at Remote pa 963.78 Log = 2.983
98 = 2.983 98
Adjusted pressure at Base pb 962.02 Log = 2.983 18 = 2.983 18
Diff = 0.000 80 = 0.000 80
Log
Diff = 4.903 09 = 4.903 09
Tabular value for KTv(24°C)= 4.817 54 = 4.301 56
1.720 63= 1.204 65
Diff height = -52.6ft = -16.02m
Check
52.6 x 0.3048 = 16.03m
which also agrees with the previous calculations.
In the above log calculation, once the difference between log pa and log pb has been obtained, the balance of the
calculation may be done by machine if the difference log pa - log pb is left in log
form, thus:-
Diff. x
Temperature Absolute °C x 221.266 = difference height in feet, where 221.266 (67,442
metres) is the constant given in the Smithsonian Meteorological
Tables, 1958 edition page 203, for use with the log formula.
The above example, using a
machine, reverts to:
0.00080 * (24 +273) * 221.266 =
52.57 ft or 16.02m.
Or taking KTv from the
Table 0.00080 * 65696 = 52.56 ft or 0.00080 * 20024 = 16.02 m.
|
TABLE OF
TEMPERATURE CONSTANT TO GIVE HEIGHT IN FEET - LOG COMPUTATION
|
|
Log KTv = log
(221.2 *(°C + 273))
|
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
|
0
|
4.78095
|
12
|
4.79963
|
24
|
4.81754
|
36
|
4.83474
|
|
0.5
|
4.78174
|
12.5
|
4.80039
|
24.5
|
4.81827
|
36.5
|
4.83545
|
|
1
|
4.78254
|
13
|
4.80115
|
25
|
4.81900
|
37
|
4.83615
|
|
1.5
|
4.78333
|
13.5
|
4.80191
|
25.5
|
4.81973
|
37.5
|
4.83685
|
|
2
|
4.78412
|
14
|
4.80267
|
26
|
4.82046
|
38
|
4.83755
|
|
2.5
|
4.78491
|
14.5
|
4.80342
|
26.5
|
4.82118
|
38.5
|
4.83824
|
|
3
|
4.78569
|
15
|
4.80418
|
27
|
4.82191
|
39
|
4.83894
|
|
3.5
|
4.78648
|
15.5
|
4.80493
|
27.5
|
4.82263
|
39.5
|
4.83964
|
|
4
|
4.78726
|
16
|
4.80568
|
28
|
4.82335
|
40
|
4.84033
|
|
4.5
|
4.78805
|
16.5
|
4.80643
|
28.5
|
4.82407
|
40.5
|
4.84102
|
|
5
|
4.78883
|
17
|
4.80718
|
29
|
4.82479
|
41
|
4.84171
|
|
5.5
|
4.78961
|
17.5
|
4.80793
|
29.5
|
4.82551
|
41.5
|
4.84241
|
|
6
|
4.79039
|
18
|
4.80868
|
30
|
4.82623
|
42
|
4.84310
|
|
6.5
|
4.79117
|
18.5
|
4.80942
|
30.5
|
4.82694
|
42.5
|
4.84378
|
|
7
|
4.79194
|
19
|
4.81017
|
31
|
4.82766
|
43
|
4.84447
|
|
7.5
|
4.79272
|
19.5
|
4.81091
|
31.5
|
4.82837
|
43.5
|
4.84516
|
|
8
|
4.79349
|
20
|
4.81165
|
32
|
4.82908
|
44
|
4.84584
|
|
8.5
|
4.79426
|
20.5
|
4.81239
|
32.5
|
4.82980
|
44.5
|
4.84653
|
|
9
|
4.79503
|
21
|
4.81313
|
33
|
4.83051
|
45
|
4.84721
|
|
9.5
|
4.79580
|
21.5
|
4.81387
|
33.5
|
4.83122
|
45.5
|
4.84789
|
|
10
|
4.79657
|
22
|
4.81461
|
34
|
4.83192
|
46
|
4.84858
|
|
10.5
|
4.79734
|
22.5
|
4.81534
|
34.5
|
4.83263
|
46.5
|
4.84926
|
|
11
|
4.79810
|
23
|
4.81608
|
35
|
4.83334
|
47
|
4.84994
|
|
11.5
|
4.79887
|
23.5
|
4.81681
|
35.5
|
4.83404
|
47.5
|
4.85061
|
|
TABLE OF
TEMPERATURE CONSTANT TO GIVE HEIGHT IN FEET
|
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
|
0
|
60388
|
12
|
63042
|
24
|
65696
|
36
|
68351
|
|
0.5
|
60498
|
12.5
|
63153
|
24.5
|
65807
|
36.5
|
68461
|
|
1
|
60609
|
13
|
63263
|
25
|
65918
|
37
|
68572
|
|
1.5
|
60719
|
13.5
|
63374
|
25.5
|
66028
|
37.5
|
68683
|
|
2
|
60830
|
14
|
63484
|
26
|
66139
|
38
|
68793
|
|
2.5
|
60941
|
14.5
|
63595
|
26.5
|
66249
|
38.5
|
68904
|
|
3
|
61051
|
15
|
63706
|
27
|
66360
|
39
|
69014
|
|
3.5
|
61162
|
15.5
|
63816
|
27.5
|
66471
|
39.5
|
69125
|
|
4
|
61272
|
16
|
63927
|
28
|
66581
|
40
|
69236
|
|
4.5
|
61383
|
16.5
|
64037
|
28.5
|
66692
|
40.5
|
69346
|
|
5
|
61494
|
17
|
64148
|
29
|
66802
|
41
|
69457
|
|
5.5
|
61604
|
17.5
|
64259
|
29.5
|
66913
|
41.5
|
69567
|
|
6
|
61715
|
18
|
64369
|
30
|
67024
|
42
|
69678
|
|
6.5
|
61825
|
18.5
|
64480
|
30.5
|
67134
|
42.5
|
69789
|
|
7
|
61936
|
19
|
64590
|
31
|
67245
|
43
|
69899
|
|
7.5
|
62047
|
19.5
|
64701
|
31.5
|
67355
|
43.5
|
70010
|
|
8
|
62157
|
20
|
64812
|
32
|
67466
|
44
|
70120
|
|
8.5
|
62268
|
20.5
|
64922
|
32.5
|
67577
|
44.5
|
70231
|
|
9
|
62378
|
21
|
65033
|
33
|
67687
|
45
|
70342
|
|
9.5
|
62489
|
21.5
|
65143
|
33.5
|
67798
|
45.5
|
70452
|
|
10
|
62600
|
22
|
65254
|
34
|
67908
|
46
|
70563
|
|
10.5
|
62710
|
22.5
|
65365
|
34.5
|
68019
|
46.5
|
70673
|
|
11
|
62821
|
23
|
65475
|
35
|
68130
|
47
|
70784
|
|
11.5
|
62931
|
23.5
|
65586
|
35.5
|
68240
|
47.5
|
70895
|
|
TABLE OF
TEMPERATURE CONSTANT TO GIVE HEIGHT IN METRES - LOG COMPUTATION
|
|
Log KTv = log
(221.2 * 0.3048 * (°C + 273))
|
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
|
0
|
4.26496
|
12
|
4.28364
|
24
|
4.30156
|
36
|
4.31876
|
|
0.5
|
4.26576
|
12.5
|
4.28441
|
24.5
|
4.30229
|
36.5
|
4.31946
|
|
1
|
4.26655
|
13
|
4.28517
|
25
|
4.30302
|
37
|
4.32016
|
|
1.5
|
4.26734
|
13.5
|
4.28592
|
25.5
|
4.30374
|
37.5
|
4.32086
|
|
2
|
4.26813
|
14
|
4.28668
|
26
|
4.30447
|
38
|
4.32156
|
|
2.5
|
4.26892
|
14.5
|
4.28744
|
26.5
|
4.30520
|
38.5
|
4.32226
|
|
3
|
4.26971
|
15
|
4.28819
|
27
|
4.30592
|
39
|
4.32295
|
|
3.5
|
4.27050
|
15.5
|
4.28895
|
27.5
|
4.30664
|
39.5
|
4.32365
|
|
4
|
4.27128
|
16
|
4.28970
|
28
|
4.30737
|
40
|
4.32434
|
|
4.5
|
4.27206
|
16.5
|
4.29045
|
28.5
|
4.30809
|
40.5
|
4.32504
|
|
5
|
4.27284
|
17
|
4.29120
|
29
|
4.30881
|
41
|
4.32573
|
|
5.5
|
4.27363
|
17.5
|
4.29195
|
29.5
|
4.30953
|
41.5
|
4.32642
|
|
6
|
4.27440
|
18
|
4.29269
|
30
|
4.31024
|
42
|
4.32711
|
|
6.5
|
4.27518
|
18.5
|
4.29344
|
30.5
|
4.31096
|
42.5
|
4.32780
|
|
7
|
4.27596
|
19
|
4.29418
|
31
|
4.31167
|
43
|
4.32849
|
|
7.5
|
4.27673
|
19.5
|
4.29493
|
31.5
|
4.31239
|
43.5
|
4.32917
|
|
8
|
4.27751
|
20
|
4.29567
|
32
|
4.31310
|
44
|
4.32986
|
|
8.5
|
4.27828
|
20.5
|
4.29641
|
32.5
|
4.31381
|
44.5
|
4.33054
|
|
9
|
4.27905
|
21
|
4.29715
|
33
|
4.31452
|
45
|
4.33123
|
|
9.5
|
4.27982
|
21.5
|
4.29789
|
33.5
|
4.31523
|
45.5
|
4.33191
|
|
10
|
4.28059
|
22
|
4.29862
|
34
|
4.31594
|
46
|
4.33259
|
|
10.5
|
4.28135
|
22.5
|
4.29936
|
34.5
|
4.31665
|
46.5
|
4.33327
|
|
11
|
4.28212
|
23
|
4.30009
|
35
|
4.31735
|
47
|
4.33395
|
|
11.5
|
4.28288
|
23.5
|
4.30082
|
35.5
|
4.31806
|
47.5
|
4.33463
|
|
TABLE OF
TEMPERATURE CONSTANT TO GIVE HEIGHT IN METRES
|
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
Deg C
|
K
|
|
0
|
18406
|
12
|
19215
|
24
|
20024
|
36
|
20833
|
|
0.5
|
18440
|
12.5
|
19249
|
24.5
|
20058
|
36.5
|
20867
|
|
1
|
18474
|
13
|
19283
|
25
|
20092
|
37
|
20901
|
|
1.5
|
18507
|
13.5
|
19316
|
25.5
|
20125
|
37.5
|
20934
|
|
2
|
18541
|
14
|
19350
|
26
|
20159
|
38
|
20968
|
|
2.5
|
18575
|
14.5
|
19384
|
26.5
|
20193
|
38.5
|
21002
|
|
3
|
18608
|
15
|
19417
|
27
|
20227
|
39
|
21036
|
|
3.5
|
18642
|
15.5
|
19451
|
27.5
|
20260
|
39.5
|
21069
|
|
4
|
18676
|
16
|
19485
|
28
|
20294
|
40
|
21103
|
|
4.5
|
18710
|
16.5
|
19519
|
28.5
|
20328
|
40.5
|
21137
|
|
5
|
18743
|
17
|
19552
|
29
|
20361
|
41
|
21170
|
|
5.5
|
18777
|
17.5
|
19586
|
29.5
|
20395
|
41.5
|
21204
|
|
6
|
18811
|
18
|
19620
|
30
|
20429
|
42
|
21238
|
|
6.5
|
18844
|
18.5
|
19653
|
30.5
|
20463
|
42.5
|
21272
|
|
7
|
18878
|
19
|
19687
|
31
|
20496
|
43
|
21305
|
|
7.5
|
18912
|
19.5
|
19721
|
31.5
|
20530
|
43.5
|
21339
|
|
8
|
18946
|
20
|
19755
|
32
|
20564
|
44
|
21373
|
|
8.5
|
18979
|
20.5
|
19788
|
32.5
|
20597
|
44.5
|
21406
|
|
9
|
19013
|
21
|
19822
|
33
|
20631
|
45
|
21440
|
|
9.5
|
19047
|
21.5
|
19856
|
33.5
|
20665
|
45.5
|
21474
|
|
10
|
19080
|
22
|
19889
|
34
|
20698
|
46
|
21508
|
|
10.5
|
19114
|
22.5
|
19923
|
34.5
|
20732
|
46.5
|
21541
|
|
11
|
19148
|
23
|
19957
|
35
|
20766
|
47
|
21575
|
|
11.5
|
19181
|
23.5
|
19991
|
35.5
|
20800
|
47.5
|
21609
|
12.10 Computation, Meridian
Transit Observation for Latitude & Longitude (Rimington’s Method)
This observation depends on the assumed meridian being within a
few minutes of the true meridian, and is designed so that each star is timed as
it crosses the assumed meridian. During that time the star follows a course on
which calculations can be made by the rules of simple proportion. See Section 3.10 for full
details of the actual observation.
Calculation of Longitude
Consider two stars which transit in the north & south
respectively :
Let
z1 and z11 = zenith distances of N & S stars at transit
d1
and d11 =declinations of N & S stars
dt1 and dt11 = corrections to N & S stars due to error in
assumed meridian
dA = azimuth correction due to error of assumed
meridian.
If the assumed meridian coincided with the true meridian, the
difference in the star's RAs would be exactly equal to the time interval
registered by the chronometer used (subject of course to
the latter Mean Time interval being converted to Sidereal Time).
This is rarely the case and corrections to the times of transit
for each star must be calculated and applied. When these corrections have been
applied, we have the star's RA (Local Sidereal Time) in relation to the
Chronometer time, the error of which is known in respect to the Greenwich Mean
Time (U.T.), the relation of which is known in respect to Greenwich Sidereal
Time. The difference between Local Sidereal Time & Greenwich Sidereal Time
is, of course, the Longitude.
When a star is very close to the meridian, the following
relationship holds good :
If dA is small,
dt1 = dA sin z1 sec d1 (1)
dt11 = dA sin z11 sec d11 (2)
Dividing (1) by (2) :
dt1 = sin z1 sec d1
dt11 sin z11 sec d11
Whence : dt1 = T sin z1 sec d1
sin z1 sec d1 + sin z11 sec d11
dt11 = T sin
z11 sec d11
sin z1 sec d1 + sin z11 sec d11
Where T = dt1 + dt11 = amount of time obtained by subtracting the
difference of RAs of N & S stars of a pair from the difference of the
Chronometer times of transits of N & S stars of the pair. (Chronometer
times corrected to Sidereal).
By adding (1) and (2), and transposing :
dA (Seconds of Arc) = _________15T__________ {If T is expressed in}
sin z1 sec d1 + sin z11 sec d11 {seconds
of time. }
In the above formula, it is seen that when T is known, the values
of dt1, dt11 and dA are obtained by the rule of simple proportion. A slide rule
will give the necessary accuracy.
The sign of the correction to be applied to the transit of each star is obtained by the following
rule :
If the chronometer time is too small, the correction to the leading star is negative, and conversely, if the chronometer interval is too large, the correction to the leading star is positive. The sign of the
correction to the following star is always opposite to that of the leading star.
See Figures 12.10(a), (b), and (c), for calculations of three pair
of stars for both Latitude and Longitude.
Azimuth
The dA is found in the Longitude calculation to ensure that an
error was not made in setting out the assumed azimuth. If the assumed azimuth
is too far from the true azimuth it is obvious that the Latitude would be
unreliable, the ZD of the Stars being read both well before and well after
Upper Transit. If the sign of the azimuth correction is required for any reason, it can be
ascertained by the following rule :
If a correction has to be added to the time of the Northern star
to find its time of Upper Transit, i.e., the star is too early, then the
assumed meridian is to the east of the true meridian and vice versa; if a
correction has to be subtracted from the time of the Northern star to find its time of Upper Transit, i.e., the star is too
late, the assumed meridian it to the west of the true meridian.
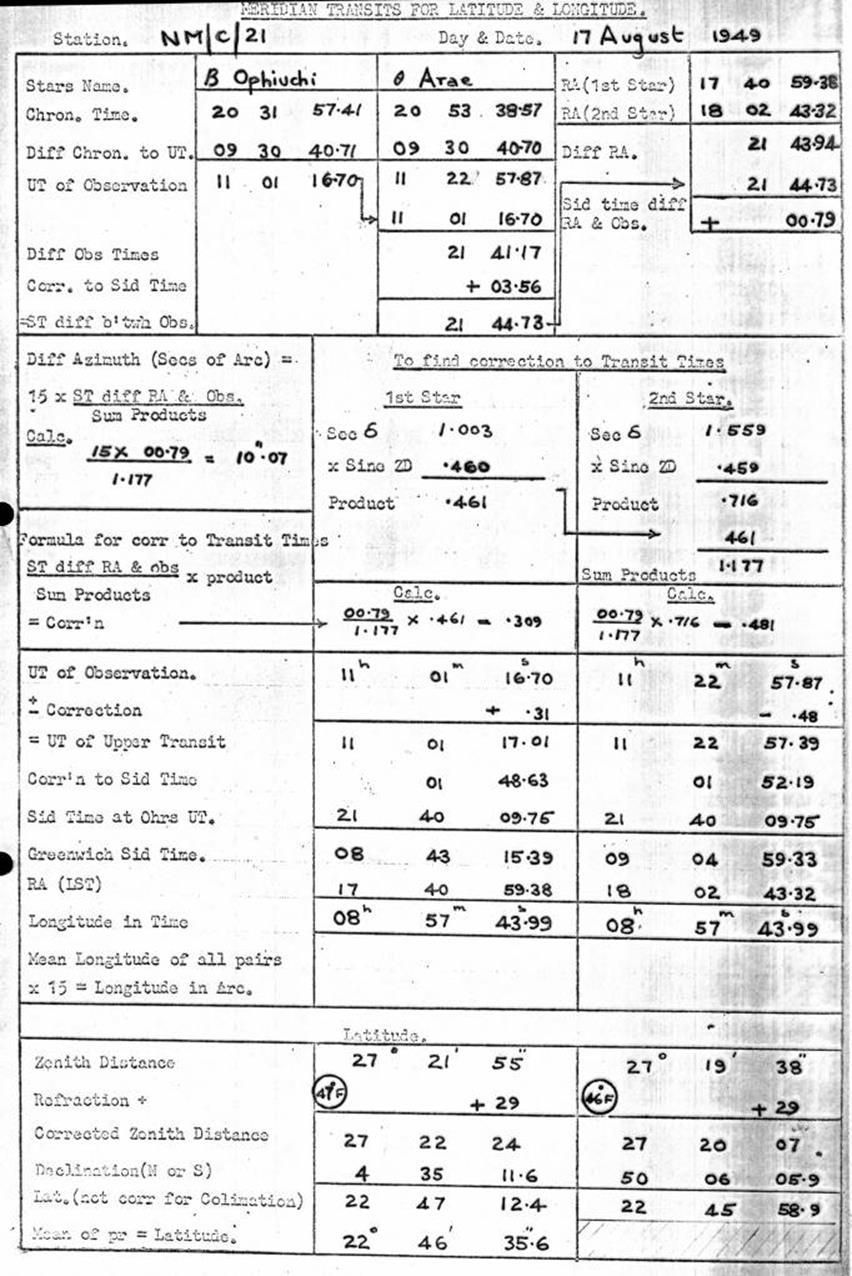
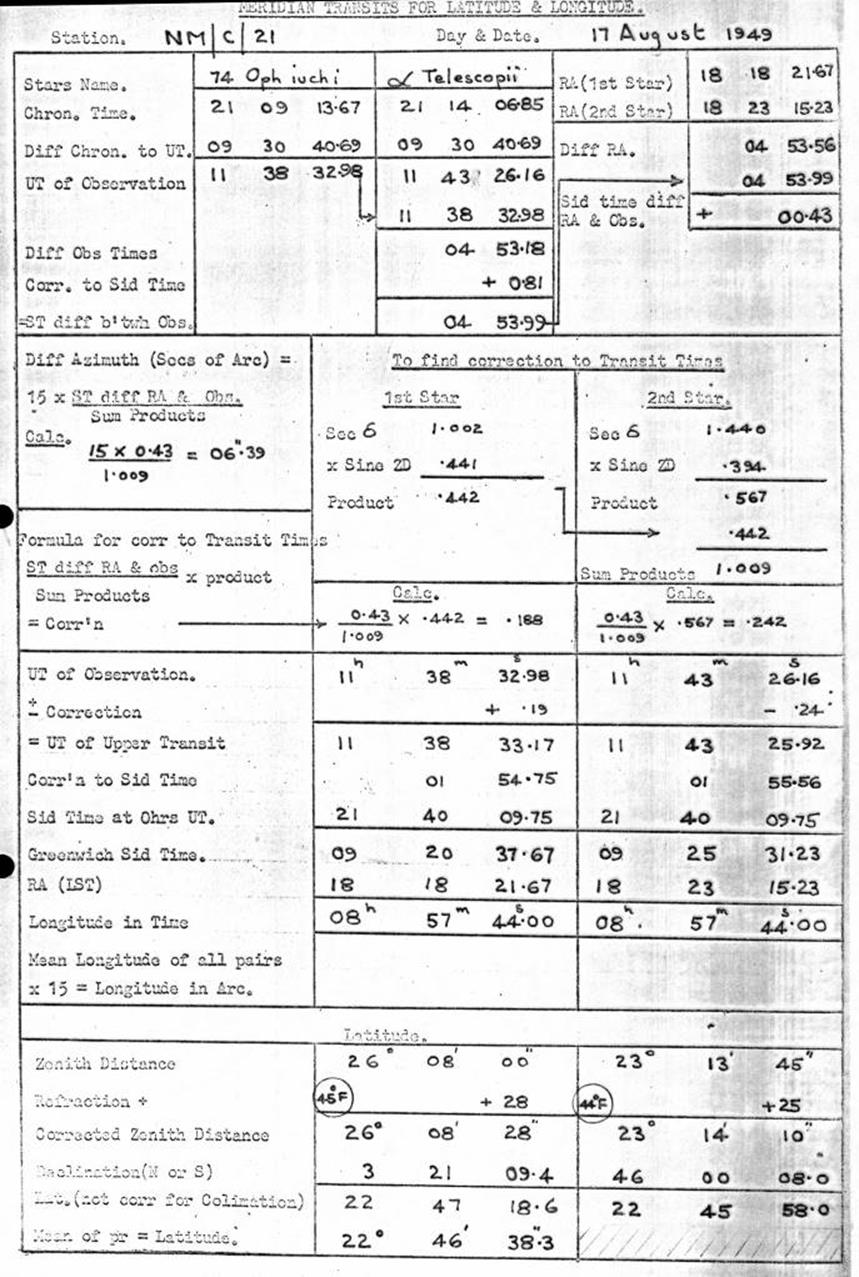
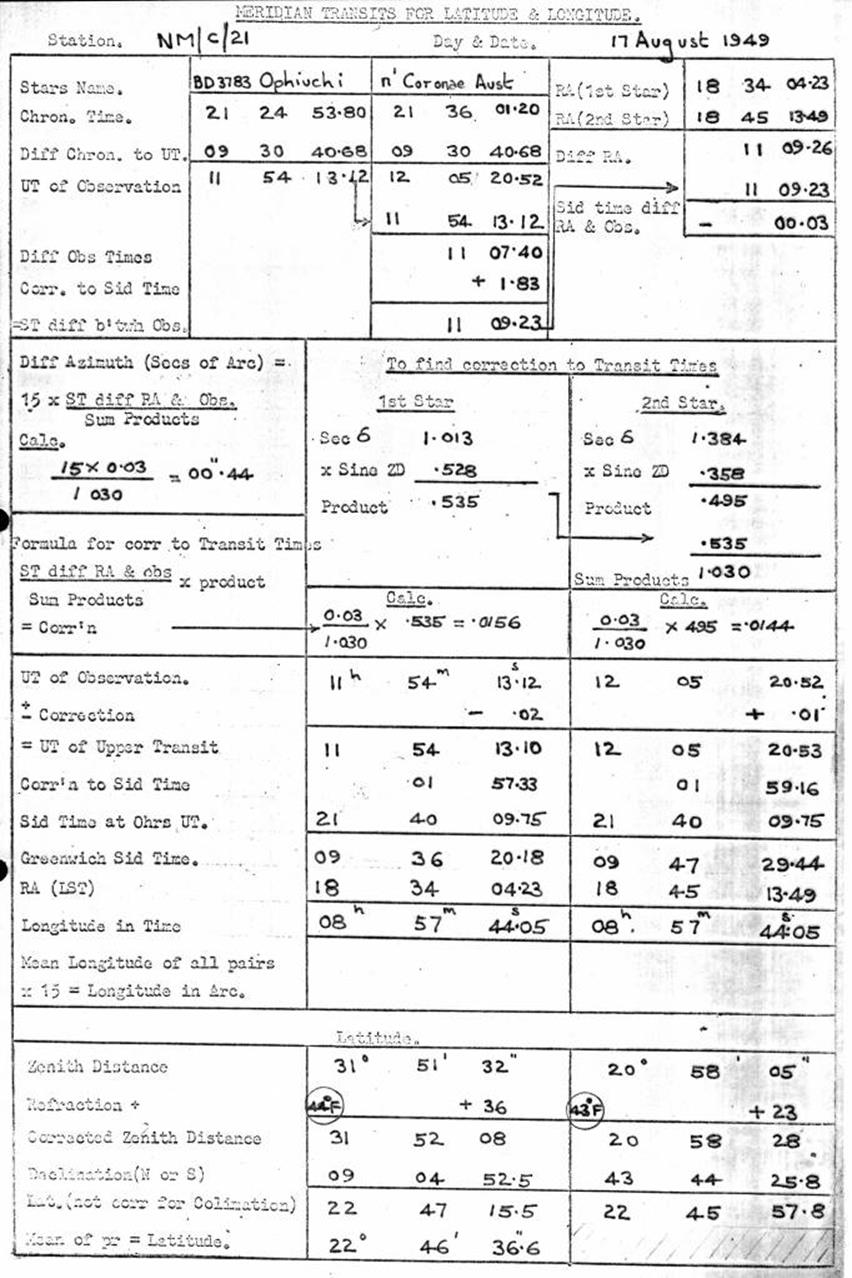
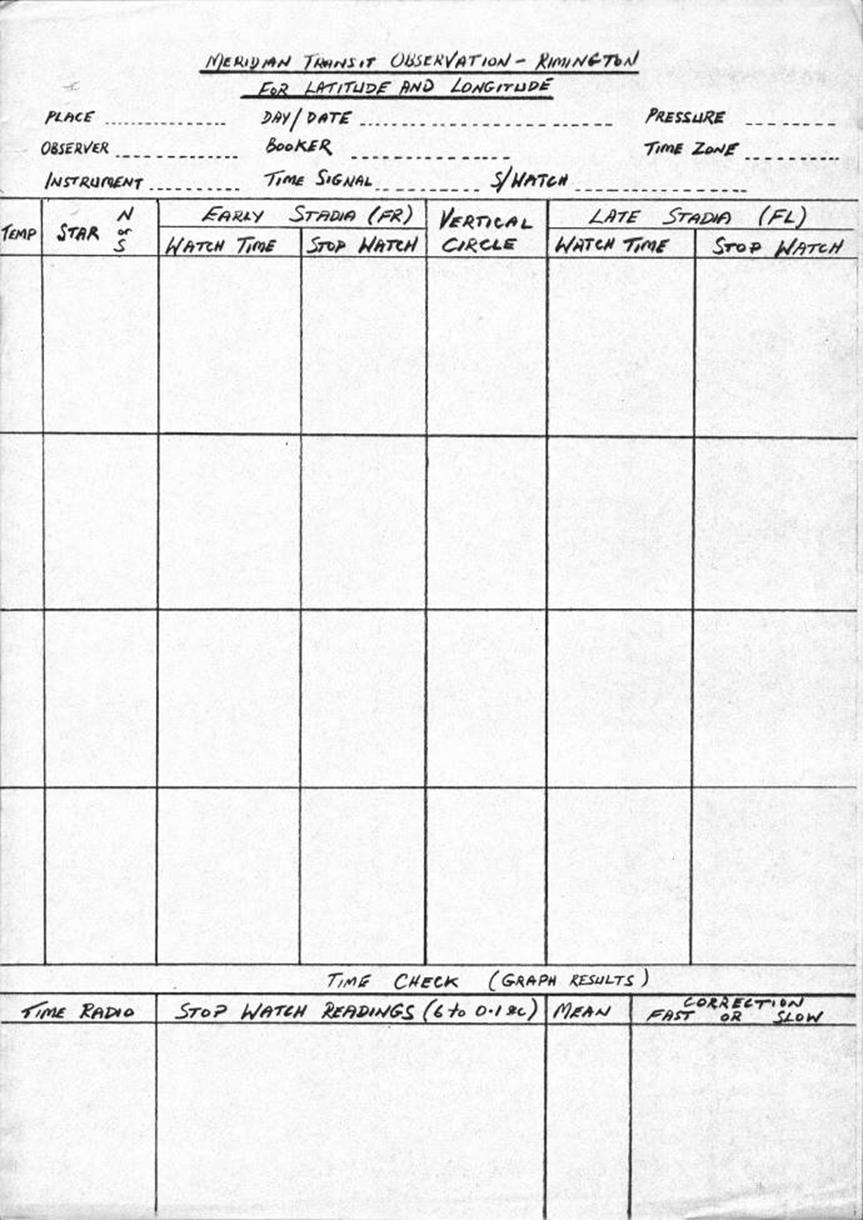
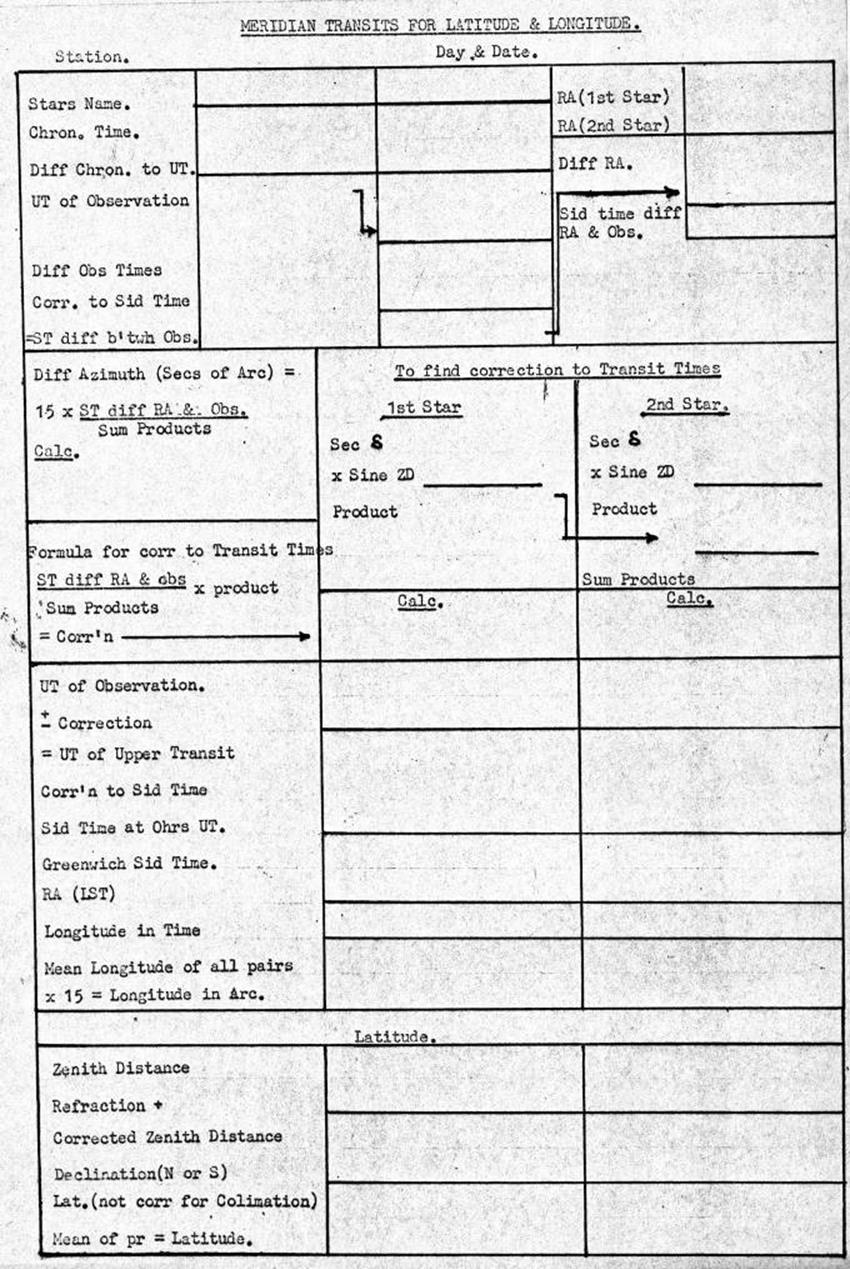
12.11 Almucantar observation for Longitude
computation
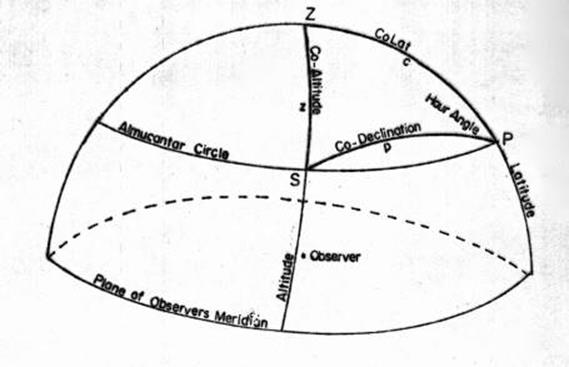
Figure
12.11.(a)
Formula :
In Figure 12.11.(a), Z is the
zenith, P is the South celestial Pole and S is the star crossing the Almucantar
circle.
Longitude is calculated by
solving the above astronomical triangle to obtain the Hour Angle when all the spherical sides
are known, i.e. :
ZS Co-Altitude (from
setting Almucantar Circle, usually 30° or 35° Altitude)
ZP Co-Latitude (from
Latitude Observation)
SP Co-Declination or Polar
Distance (90° ± Declination, from FK4).
The Tan formula is most
suitable because of its more sensitive value and is regularly used in Sun Observations
to find both the Hour and the Azimuth Angles :
Tan(A/2) = √{
(sin(s-b)*sin(s-c)) / (sin s * sin(s-a)) }
In this observation, where
only the Hour Angle is required and applying it to the triangle Z.P.S. in
Figure 12.11 (a), the formula can be written thus:-
Tan(HA/2) = √{
(sin(s-c)*sin(s-p)) / (sin s * sin(s-z)) }
where :
HA/2 = half the Hour
Angle.
p = Co-Declination or
Polar Dist. (c in original formula)
c = Co-Latitude (b
in original formula)
z = Co-Altitude (a in original
formula)
Working through the
proforma
As explained in 3.12, the
exact vertical angle of 30° or 35° (plus refraction) is set, and this will
remain constant throughout the whole observation. However, as the alidade
bubble would not remain constant for this whole period, it is deliberately
moved with the single footscrew after each pointing. The mean of the five
bubble readings taken is divided by five and must now be used in the
computation.
(i) Convert bubble from arc to
time
The value of one division
of the T3 alidade bubble is about 6 seconds of arc; divide this by 15 and
multiply by secant Latitude and Cosecant of the approximate azimuth to get the
value of one division in seconds of time. This is done for an azimuth of 90°
and also for 80° and 100° to cover the various bearings of the stars used in
this observation. Interpolate for the bearing of each star observed; this value
is multiplied by the mean bubble correction from the field book.
(ii) Sign of the bubble
correction
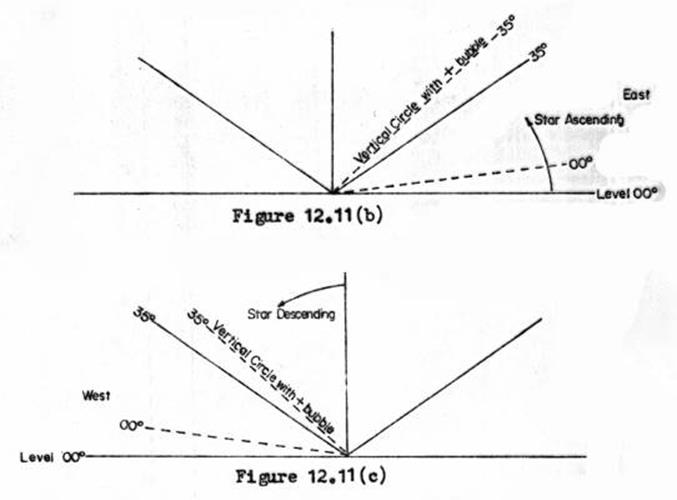
East stars
The broken line in Figure 12.11(b) shows what happens when the
bubble is moved to a plus reading with footscrew; it is clear that the
ascending East star will arrive late and the correction necessary to give the
exact time it reached 35° altitude will be Minus. Just as obviously, if the
bubble was moved to a minus reading with the footscrew, the star will arrive
early and the correction will be Plus.
West stars
With the bubble giving a plus reading as in Figure 12.11(c) the
descending West star will arrive early and it is clear that the correction to
give the exact time it will reach 35° altitude will be Plus; and obviously if
the bubble is moved to a minus reading the star will arrive late and the
correction will be Minus.
Interpolation of R.A. & Declination from FK4
The interpolation by first
differences shown in the first 'step below is accurate enough for field
computations. The use of second differences in the second step shows the
requirement for office computations prior to the advent of the computer.
1. In the FK4, the R.A. &
Declination is shown at 10 day intervals, (sometimes 9.9) in U.T., by date and
decimal of a day.
2. Turn U.T. of observation
to a decimal of a day.
3. Look up R.A. (or
Declination) for the dates which bracket the observation and interpolate for
day (including decimal) required.
4. When calculating Second
Differences, the interpolation must be made by utilizing the tabular
differences over 30 days, i.e., the 10 days previous to and the 10 days
following the 10 day period which brackets the observation. The following
extract from the FK4 shows the requirement. To make for ease in the
calculation, the tabular differences are called "a”, “b” and
"c", as indicated; the proportion of the 10 day interval required is
called "n”.
Extract from FK4,
April-May 1975 Star No. 188
RA Declination
iv 9.7 5h
06m 38.073s -5° 06' 73.60”
-129 (called
a) +63*(called a)
iv 19.6
37.944 72.97
-093 (called
b) +84 (called b)
iv 29.6 37.851 72.13
-057 (called
c) +104 (called c)
v 9.6 37.794 71.09
Example : Date
of Observation 26 April 1975
Calculation of
"n" (Required for calculating both 1st & 2nd Differences)
U.T of
Observation was 19h 26m 24s = 19.44/24 = 0d.81 therefore day and decimal of
observation was 26.81d.
Proportion of
10 day interval is : [Day of Obs(26.81) - Day listed (19.6)]/10 which gives
0.721 (called "n”).
Calculation using First
Differences
RA Declination
0.093 x 0.721
= 0.067 (RA increment) 0.84 x 0.721 = 0.61 (Decl increment)
iv 19.6 5h
06m 37.944s 5° 06' 72.97”
-0.067
-0.61
iv
26.81 5h 06m 37.877s 5° 06’ 72.36”
* Watch signs in
Declination example on next page. With star of Minus Declination (South Stars),
where the increment is decreasing the sign of the increment is listed Plus and
vice versa. With stars of Plus Declination (North Stars) this problem does not
exist.
Calculation using Second
Differences
RA :
Find (c-a) : this becomes
the "horizontal value" to be looked up in the FX4 (Table vi) while
"n" is the "vertical value" to be looked up in the same
Table.
c a
(c-a) = -0.057
- (-0.129) = +0.072 and "n" is 0.721.
These figures give 4 from
the table, which is .004s and the sign is Minus because it is always opposite
to (c-a).
RA (from First
Differences) 5h 06m 37.877s
-0.004
RA (from
Second Differences) 5h 06m 37.873s
Declination :
Proceed as with RA
calculation but watch signs (*) here; the declination is gradually decreasing
so the signs are minus.
c a
(c-a) = -1.040
- (-0.630) = -0.41 and "n" is 0.721.
These figures give 2 from
the Table which is .02” and the sign is Plus, i.e., opposite to (c-a).
Dec. (from
First Differences) -5° 06' 72.36”
+0.02
Dec (from
Second Differences) -5° 06' 72.38”
Sometimes the case arises
where there is a change of sign in one of the group of increments from which
the interpolation of Second Differences is being made, for example :
The
Declination of Star No. 436 is required at U.T 08h 12m 00s on 22 June 1975
(22.3d).
Extract from
FK44 – 1975
vi 8.8
Declination -62° 52' 86.56”
-0.17 (a)
vi 18.7 86
.73
+0.33 (b)
vi 28.7 86
.40
+0.82 (c)
vi 8.7 85
.58
Proportion of
10 day interval :
(Day of Obs
(22.3) - Day listed (18.7)) / 10 = 3.6/10 = 0.36 (“n”).
In the extract of the
declination above, it is noticed that on June 8.8 the seconds are 86.56 and
increase by 0.17 to 86.73, then decrease by 0.33 to 86.40 and again by 0.82 to
85.58. This means that the 0.17 is plus and then 0.33 and 0.82 are minus,
therefore :
(c-a) = - 0.82
-(+0.17) which is - 0.99
From the FK4 Table vi,
with the "horizontal value" 0.99 and the "vertical value"
0.36, the tabular figure is 6 which gives the Second Difference as 0.06 and the
sign is Plus, ie., opposite to (c-a). The First Difference is found as usual
and then the Second Difference applied :
vi 18.7d Declination -62°
52' 86.73”
First Diff
increment -0.12 (incr. = 0.33 * 0.36 =0.12)
-62° 52’
86.61”
Second Diff
increment +0.06
Declination
required -62° 52’ 86.67”
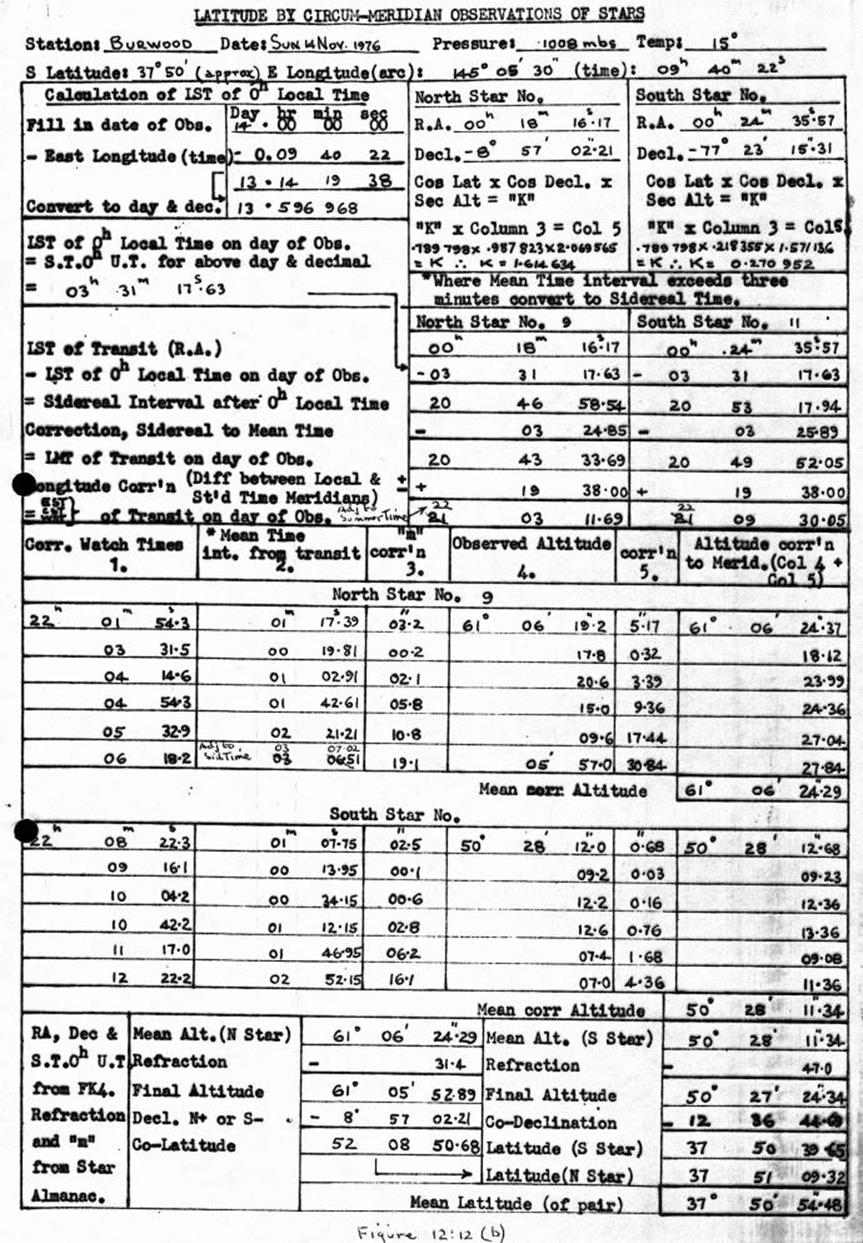
12.12 Latitude by Circum-Meridian Altitudes
computation
A series of
observations are taken on each star as explained in 3.13. Observations should
commence no earlier and cease no later than 3 minutes from transit, with the
attempt being made to have 3 observations on each side of transit. The
observations are all on the same theodolite face and are balanced with similar
observations on another star of equivalent altitude which bears 180° from the
star initially observed. Figure 12.12(a) illustrates the method.
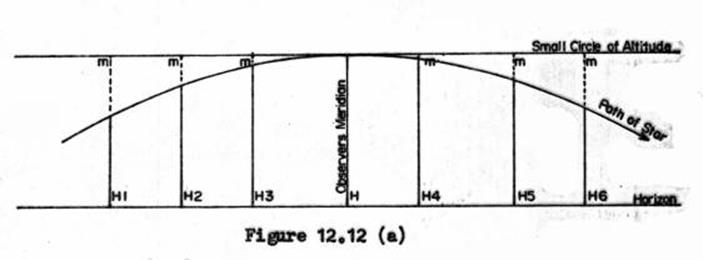
As shown above, when a
star is close to transit, the small circle of altitude and the horizon can be
considered parallel lines, as also can the altitudes H and HI to H6. Thus the
requirement is to calculate the correction "m" for each observation
so that when "m" is added to the observed altitude, the result is as
though the actual observations were all taken at the time of transit. Knowing
the accurate Longitude, from the FK4 it is easy to ascertain the time of
transit of the star and using a stopwatch and time signal it is easy to
ascertain the time of each observation. Using the small time difference between
times of observation and transit, (i.e., Hour Angle) "m" can be found
from a table in the Star Almanac, (or a more comprehensive table in
"Close").
The formula for this table
is :
Correction
(seconds of arc) = 2*Sin2(½HA) / Sin 1" where ½HA is secs arc.
"m" is affected
by the Latitude, also the Declination and Altitude of the star, therefore
"m" from the table must be multiplied by a factor "k"
obtained from :
Cos Lat x Cos
Dec. x Sec. Alt.
The calculation is easy
but must be methodically laid out as a separate "m" for each of the
six observations must be read from the Table and then multiplied by
"k" before applying the correction to each of the observations.
The attached proforma is
ideal, as the worked example shows.